Ранг матрицы.

Решение однородных СЛАУ

Методические указания для проведения упражнений

по курсу аналитической геометрии

Калуга 2011г.

Содержание.

Цели занятия стр.4

План занятия стр.4

Необходимые теоретические сведения стр.5

Практическая часть стр.10

Контроль освоения пройденного материала стр.13

Домашнее задание стр.14

Количество часов: 2

Цели занятия:

1. Систематизировать полученные теоретические знания о видах СЛАУ и способах их решения.

2. Получить навыки решения однородных СЛАУ.

План занятия:

1. Кратко изложить теоретический материал.

2. Решить однородную СЛАУ.

3. Найти фундаментальную систему решений однородной СЛАУ.

4. Найти частное решение однородной СЛАУ.

5. Сформулировать алгоритм решения однородной СЛАУ.

6. Проверить выполнение текущего домашнего задания.

7. Провести проверочную работу.

8. Представить тему следующего семинара.

9. Выдать текущее домашнее задание.

Необходимые теоретические сведения.

Ранг матрицы.

Опр.Рангом матрицы называют число, которое равно максимальному порядку среди ее ненулевых миноров. Ранг матрицы обозначают .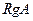

Если квадратная матрица невырождена, то ранг равен ее порядку. Если квадратная матрица вырождена, то ее ранг меньше ее порядка.

Ранг диагональной матрицы равен количеству ее ненулевых диагональных элементов.

Теор. При транспонировании матрицы ее ранг не меняется, т.е. .

Теор. Ранг матрицы не меняется при элементарных преобразования ее строк и столбцов.

Теорема о базисном миноре.

Опр. Минор матрицы называют базисным, если выполнены два условия:

а) он не равен нулю;

б) его порядок равен рангу матрицы .

Матрица может иметь несколько базисных миноров.

Строки и столбцы матрицы , в которых расположен выбранный базисный минор, называют базисными.

Теор. Теорема о базисном миноре. Базисные строки (столбцы ) матрицы , соответствующие любому ее базисному минору , линейно независимы. Любые строки (столбцы) матрицы , не входящие в , являются линейными комбинациями базисных строк (столбцов).

Теор. Для любой матрицы ее ранг равен максимальному количеству ее линейно независимых строк (столбцов).