
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Однородные СЛАУ.
Однородная система 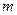 линейных алгебраических уравнений с
линейных алгебраических уравнений с  неизвестными представляет собой систему вида
неизвестными представляет собой систему вида

Однородные СЛАУ всегда совместны, поскольку всегда имеется нулевое решение.
Критерий существования ненулевого решения.Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы ее матрица была вырождена.
Теор.Если столбцы 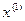 ,
,  , …,
, …, 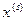 - решения однородной СЛАУ, то и любая их линейная комбинация также является решением этой системы.
- решения однородной СЛАУ, то и любая их линейная комбинация также является решением этой системы.
Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечное множество решений.
Естественно попытаться найти такие решения 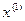 ,
,  , …,
, …, 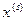 системы, чтобы любое другое решение представлялось в виде их линейной комбинации и притом единственным образом.
системы, чтобы любое другое решение представлялось в виде их линейной комбинации и притом единственным образом.
Опр. Любой набор из 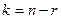 линейно независимых столбцов
линейно независимых столбцов 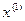 ,
,  , …,
, …,  , являющихся решениями однородной СЛАУ
, являющихся решениями однородной СЛАУ 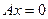 , где
, где  - число неизвестных, а
- число неизвестных, а 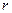 - ранг ее матрицы
- ранг ее матрицы  , называют фундаментальной системой решений этой однородной СЛАУ.
, называют фундаментальной системой решений этой однородной СЛАУ.
При исследовании и решении однородных систем линейных уравнений в матрице системы будем фиксировать базисный минор. Базисному минору будут соответствовать базисные столбцы и, следовательно, базисные неизвестные. Остальные неизвестные будем называть свободными.
Теор. О структуре общего решения однородной СЛАУ. Если 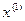 ,
,  , …,
, …,  - произвольная фундаментальная система решений однородной СЛАУ
- произвольная фундаментальная система решений однородной СЛАУ 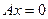 , то любое ее решение можно представить в виде
, то любое ее решение можно представить в виде
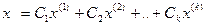 , где
, где  , …,
, …, 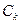 - некоторые постоянные.
- некоторые постоянные.
Т.о. общее решение однородной СЛАУ имеет вид
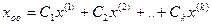 .
.
Дата добавления: 2015-04-15; просмотров: 404; Мы поможем в написании вашей работы!; Нарушение авторских прав |