
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Матричное решение задачи линейного программирования
Исходное распределение переменных на зависимые и независимые принято таким же, как и в предыдущем подходе. В результате исходная матричная структура имеет вид:

Здесь ниже строки с идентификацией 
 следует строка с коэффициентами
следует строка с коэффициентами 
 линейной формы соответственно их разделению по классам зависимых и независимых переменных, идентификация которых представлена в строке ниже. Далее идут матрицы и вектора, соответствующие системе линейных ограничений. Записанные под матрицами G, F матричные уравнения не нуждаются в комментариях.
линейной формы соответственно их разделению по классам зависимых и независимых переменных, идентификация которых представлена в строке ниже. Далее идут матрицы и вектора, соответствующие системе линейных ограничений. Записанные под матрицами G, F матричные уравнения не нуждаются в комментариях.
Отрицательный коэффициент в линейной форме наблюдается лишь у переменной х4, которая должна варьироваться.
Столбец Н формируется поэлементным делением столбца F на первый столбец матрицы G, соответствующий переменной х4, которая выводится из базиса (в случае отрицательного результата записывается  ).
).
Столбец H показывает, что из базиса должна быть выведена переменная х3. Замена столбцов х3, х4 отражена в левой части следующей структуры
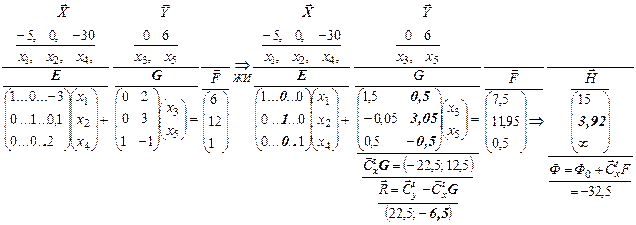
Для явного выражения зависимых переменных от независимых выполняется жорданово исключение переменных, т.е. расширенная матрица (EGF) преобразуется так, чтобы на месте соответствующей  матрицы Е была бы сформирована единичная матрица. Это выполнено в правой части структуры
матрицы Е была бы сформирована единичная матрица. Это выполнено в правой части структуры
Анализ коэффициентов при независимых переменных (строка  ) показывает, что единственный отрицательный коэффициент соответствует переменной x5, на основе чего формируется столбец Н и делается вывод о необходимости на следующем шаге замены статуса переменных x5, x2.
) показывает, что единственный отрицательный коэффициент соответствует переменной x5, на основе чего формируется столбец Н и делается вывод о необходимости на следующем шаге замены статуса переменных x5, x2.
Дальнейшие расчеты представлены в следующей структуре
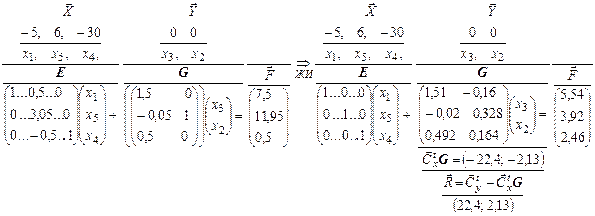 Все коэффициенты у независимых переменных положительны. В результате получено решение ЗЛП
Все коэффициенты у независимых переменных положительны. В результате получено решение ЗЛП  ,
, 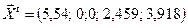 .
.
Дата добавления: 2015-04-16; просмотров: 258; Мы поможем в написании вашей работы!; Нарушение авторских прав |