
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интерпретация двойственной задачи
В то время как физическая интерпретация исходной задачи ясна, смысл двойственной задачи не столь очевиден. Возникает вопрос, как интерпретировать линейную форму и условия двойственной задачи. Лучше всего на этот вопрос можно ответить с помощью формулировки исходной и двойственной задач в терминах размерностей. Пусть рассматривается предприятие, выпускающее ряд изделий (болты, гайки, шайбы и др.). При этом используются некоторые ресурсы (сырье, материалы, финансы и др.), причем одни и те же ресурсы используются для разных видов продукции. Исходная задача заключается, например, в максимизации суммарного дохода.
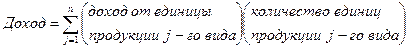
при условиях, что используемые ресурсы не превысят некоторых заданных пределов
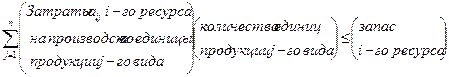 , i=1,2,…,m; j=1,2,…,n.
, i=1,2,…,m; j=1,2,…,n.
Рассмотрим, каковы должны быть размерности переменных и матриц преобразования в так называемой двойственной задаче, которая сводится к минимизации
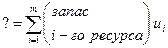
| (8.24) |
при условиях
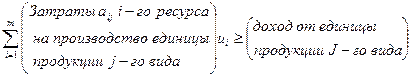
ui≥0, i=1,2,…,m; j=1,2,…,n.
Очевидно, что размерности условий двойственной задачи будут совпадать, если ui совпадет с ценой i-го ресурса (ценность ресурса в конечном продукте), а в левой части (8.24) будет суммарная стоимость всех ресурсов. Тогда двойственная задача состоит в минимизации
min 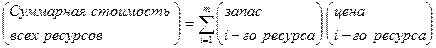
при условиях

Таким образом, задачи двойственной пары могут быть сформулированы следующим образом:
Исходная задача. Сколько единиц хj, j=1, 2, ...,n каждого вида продукции, нужно выпустить при удельном доходе сj и данном предельном потреблении каждого из имеющихся ресурсов bi, i=1, 2, ...,m, чтобы получить от всего производства максимальную прибыль?
Двойственная задача. Какой должна быть цена ui, i=1, 2, ...,m каждого из ресурсов, чтобы при максимальном их использовании (объем bi) обеспечить минимальную суммарную стоимость ресурсов, и при этом гарантировать удельные доходы не меньше заданных сj, j=1, 2, ...,n?
Двойственные переменные u именуются в различных источниках по-разному, в частности, они называются учетными, неявными или фиктивными ценами.
Дата добавления: 2015-04-16; просмотров: 236; Мы поможем в написании вашей работы!; Нарушение авторских прав |