Метод потенциалов

Построенный опорный план транспортной задачи как задачи линейного программирования можно было бы довести до оптимального с помощью симплексного метода. Однако из-за громоздкости симплексных таблиц, содержащих mn неизвестных, и большего объема вычислительных работ для получения оптимального плана используются более простые методы. Самым распространенным является метод потенциалов (модифицированный распределительный метод).

В основе данного метода лежит теорема, являющаяся, по существу, отражением теоремы двойственности применительно к транспортной задаче.

Теорема. Если план транспортной задачи является оптимальным, то ему соответствует система из m+n чисел 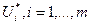и , удовлетворяющих условиям

, ;

,

(i=1,…,m; j=1,…,n)

Числа называются потенциалами соответственно поставщиков и, потребителей.

Действительно, условия

;

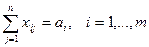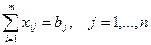
определяют m+n ограничений типа «равенство». Каждому равенству i соответствует двойственная переменная U_i. а равенству j - двойственная переменная V_j . В двойственной задаче ограничивающих условий столько, сколько переменных в основной задаче, т.е. mn. В правой части двойственного ограничения - C_ij.

В результате транспонирования матрицы коэффициентов в новой матрице в каждой строке имеются лишь две единицы, соответственно позиции i и j. Отсюда ограничение . Для большего понимания рассмотрим транспортную задачу размерностью 2х2.