КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Двойственная задача
Функция цели:
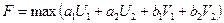
Ограничения:
≤ 
или в канонической форме 
.
Знак неравенства преобразуется в равенство только в том случае, когда соответствующая неравенству переменная xij не равна нулю. Отсюда для клетки, где 
сумма Ui+ Vj= Cij.
В представленной постановке наглядно представлена физическая сущность двойственных переменных – это некоторые потенциалы узлов. При этом если есть транспорт груза (энергии) от узла i к узлу j, то сумма потенциалов смежных узлов равна цене перевозки по рассматриваемой связи.
Из теоремы следует: для того чтобы первоначальный опорный план был оптимальным, необходимо выполнение следующих условий:
a) для каждой занятой клетки сумма потенциалов должна быть равна стоимости единицы перевозки, стоящей в этой клетке,
 ;
| (8.28) |
b) для каждой незанятой клетки сумма потенциалов должна быть меньше или равна стоимости единицы перевозки, стоящей в этой клетке
 .
| (8.29) |
Если хотя бы одна незанятая клетка не удовлетворяет условию (8.29), то опорный план является неоптимальным и его можно улучшить, вводя в базис вектор, соответствующий клетке, для которой нарушается условие оптимальности, (т.е. в клетку надо переместить некоторое количество единиц груза).
Дата добавления: 2015-04-16; просмотров: 145; Мы поможем в написании вашей работы!; Нарушение авторских прав |