Метод множителей Лагранжа

Функция Лагранжа исторически возникла в исследованиях аналитических механиков (Лагранж, Фурье, Фаркаш, Остроградский и др.) по проблеме равновесия механических систем при связях в форме уравнений и неравенств. Равновесие в механических системах сопряжено с состоянием, соответствующим минимуму потенциальной энергии. Данная функция играет ключевую роль в задачах линейного и нелинейного программирования.

Пусть задана задача математического программирования: максимизировать функцию

(9.4)

при ограничениях

.

(9.5)

Для решения задачи можно воспользоваться классическим методом отыскания условного экстремума функций нескольких переменных. При этом полагается, что функции и 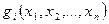непрерывны вместе со своими первыми частными производными. Для решения задачи составляется так называемая функция Лагранжа

,

(9.6)

где - множители Лагранжа, которые рассматриваются наравне с основными переменными. В классическом решении определяются и приравниваются нулю частные производные функции Лагранжа по x_j и λ_i. В результате формируется система уравнений

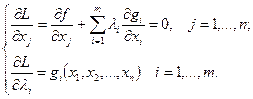
(9.7)

Если функция Ф = в точке имеет экстремум, то существует такой вектор , что точка является решением системы (9.7). Следовательно, решая систему (9.7), получаем множество точек, в которых функция Ф может иметь экстремальные значения. При этом способ определения точек глобального минимума или максимума неизвестен. Однако если найдены все решения системы, то для определения глобального максимума (минимума) достаточно сравнить значения функции в соответствующих точках.

Множитель Лагранжа имеет экономический смысл. Если под понимать «доход», соответствующий плану 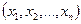а под - соответствующие тому же плану «издержки ресурса i», то величина имеет смысл цены этого ресурса. Вспомним, какой физический смысл имели двойственные переменные в линейном программировании? – Тот же самый! Отсюда множители Лагранжа можно рассматривать как некоторые двойственные переменные. В результате решение основной задачи нелинейного программирования часто может быть упрощено при использовании процедур, учитывающих свойства двойственных задач.

Можно доказать, что если рассматривать экстремум при переменном ограничении , то производная экстремального значения функционала Ф по величине ограничения с точностью до знака равна множителю Лагранжа. Иначе говоря, множитель Лагранжа характеризует скорость изменения экстремального значения целевой функции в зависимости от размера ресурса. Эта величина носит название маргинальной оценки.

Термин «маргинальный» в переводе с английского «marginal» означает предельный. При этом маргинальную оценку следует трактовать не как предельную по величине оценку, а как оценку ограничения (некоторого предела ресурса).

В общей задаче нелинейного программирования условие (9.5) принимает форму неравенства. Однако и здесь применим метод множителей Лагранжа.

Если для функций , существуют вторые частные производные и они непрерывны, то согласно теореме Куна-Таккера достаточное условие наличия локального экстремума функции в точке решения системы (9.7) имеет вид

.

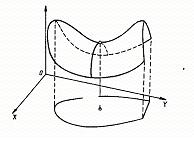
Пара векторов называется в этом случае седловой точкой функции . Такое название связано с тем, что графически (рис. 9.4) функция в окрестности точки выглядит подобно седлу. Значение этой точки очень велико. Она облегчает поиск максимума целевой функции нелинейной задачи. Вместо того чтобы специально решать задачу нелинейного программирования, можно (что зачастую проще) искать седловую точку функции Лагранжа . Зная ее, мы будем знать и решение задачи.

Ограничения общей задачи нелинейного программирования часто имеют вид:

Постоянный вектор можно интерпретировать как располагаемые ресурсы, а функции - как расход (затраты) этих ресурсов при выбранном плане 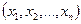. Тогда величина = с экономической точки зрения означает количество неиспользованного i-го ресурса при выбранном производственном плане. При этом функция отражает доход предприятия, соответствующий плану .

Функцию Лагранжа в этой задаче можно интерпретировать как стоимостное выражение результата производства, состоящего в получении дохода и сохранении неиспользованных ресурсов, а множители Лагранжа являются здесь оценками единицы неиспользованных ресурсов разных видов. Экономический смысл седловой точки у функции Лагранжа состоит в том, что между ценами имеющихся ресурсов и величиной дохода имеется равновесие, отклоняться от которого экономически не выгодно.

Интересно сравнить роль оценок в задачах линейного и нелинейного программирования. В линейном программировании целевые функции основной и двойственной задач в точке оптимума совпадают. Иначе обстоит дело в нелинейном программировании. Необходимое условие достижения оптимума состоит здесь в равенстве лишь приростных, дифференциальных затрат и «маргинального (предельного) эффекта».

Пример 1. Найти точку условного экстремума функции Ф = x₁x₂+х₂х₃ при ограничениях

Решение. Составим функцию Лагранжа

и продифференцируем ее по переменным . Приравнивая производные нулю, получаем следующую систему линейных уравнений:

Решение данной СЛУ, а следовательно и поставленной задачи: x₁ = х₂ = x₃ = 1, Ф = 2.