ЗЛП как частный случай ЗНП

Рассмотрим функцию Лагранжа для стандартной задачи линейного программирования. Здесь = , = , .

Соотношения (9.16)-(9.18) применительно к ЗЛП позволяют сделать некоторые обобщения . В частности, задача максимизации легко трансформируется в задачу на отыскание минимума. Необходимо только в ОДЗ поменять знак неравенств (табл. 9.2).

Таблица 9.2

ОЗЛП:	ДЗЛП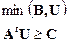
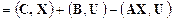
Аналог:	Аналог:

Представленная таблица еще раз показывает, что функция Лагранжа основной и двойственной как нелинейного, так и линейного программирования совпадают (поскольку ).

Заметим, что правило перехода к двойственной задаче в верхней строке схемы согласуется с правилом перехода в нижней строчке.

Применительно к основной ЗЛП

Последнее равенство соответствует функции Лагранжа для задачи (9.17), если рассматривать в качестве переменных вектор , в качестве ограничений , а в качестве вектора множителей Лагранжа - , но это двойственная задача ЛП:

,