Свойства средней арифметической

Средняя арифметическая обладает рядом свойств, знание которых необходимо для понимания сущности средних, а также для упрощения их вычисления.

1. Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических величин:

Если 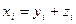, то

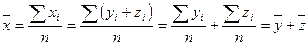(2.18)

Это правило показывает, в каких случаях можно суммировать средине величины. Если, например, выпускаемые изделия состоят из двух деталей у и z и на изготовление каждой из них расходуется в среднем у = 3ч, z = 5ч, то средние затраты времени на изготовление одного изделия (х), будут равны: 3 + 5 = 8ч., т.е. х = у = z.

2. Алгебраическая сумма отклонений индивидуальных значений признака от средней равна нулю, так как сумма отклонений в одну сторону погашается суммой отклонений в другую, т.е. , , потому что

(2.19)

Это правило показывает, что средняя является равнодействующей.

3. Если все варианты ряда уменьшить или увеличить на одно и тоже число а, то средняя уменьшится или увеличится на это же число а:

. (2.20)

4. Если все варианты ряда уменьшить или увеличить в А раз, то средняя также уменьшится или увеличится в А раз:

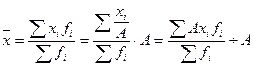. (2.21)

5. Если все частоты ряда разделить или умножить на одно и тоже число d, то средняя не изменится:

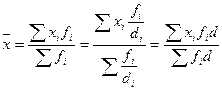. (2.22)

Это свойство показывает, что средняя зависит не от размеров весов, а от соотношения между ними. Следовательно, в качестве весов могут выступать не только абсолютные, но и относительные величины.

Вопросы для самоконтроля

1. Какое значение имеет средняя величина в статистике?

2. Перечислите виды и формы средних величин

3. Как исчисляется средняя арифметическая простая и взвешенная?

4. Как исчисляется средняя гармоническая простая и взвешенная?

5. Как исчисляется средняя геометрическая?