Относительные показатели, их роль и типология

В статистике относительные показатели используют в сравнительном анализе, в обобщении и синтезе.

Относительные показатели - это цифровые обобщающие показатели, они есть результат сопоставления двух статистических величин.

По своей природе относительные величины производны от деления текущего (сравниваемого) абсолютного показателя на базисный показатель.

Относительные показатели могут быть получены или как соотношения одноименных статистических показателей, или как соотношения разноименных статистических показателей. В первом случае получаемый относительный показатель рассчитывается или в процентах, или в относительных единицах, или в промилле (в тысячных долях). Если соотносятся разноименные абсолютные показатели, то относительный показатель в большинстве случаев бывает именованным.

В зависимости от величин числителя и знаменателя этой дроби относительные величины могут быть выражены в таких формах: коэффициентах (частях), процентах (%), промилле ( 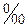), продецимилле ( ), когда за базу сравнения принимают соответственно 1, 100, 1000, 10000 единиц.

Относительные величины, используемые в статистической практике:

* относительная величина структуры;

* относительная величина координации;

* относительная величина планового задания;

* относительная величина выполнения плана;

* относительная величина динамики;

* относительная величина сравнения;

* относительная величина интенсивности.

Относительная величина структуры (ОВС) характеризует структуру совокупности, определяет долю (удельный вес) части в общем объёме совокупности.

ОВС рассчитывают как отношение объёма части совокупности к абсолютной величине всей совокупности, определяя тем самым удельный вес части в общем объёме совокупности (%):

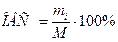(2.7)

где m_i - объём исследуемой части совокупности;

M - общий объём исследуемой совокупности.

Относительная величина координации (ОВК) характеризует соотношение между двумя частями исследуемой совокупности, одна из которых выступает как база сравнения (%):

, (2.8)

где m_i - одна из частей исследуемой совокупности;

m_б - часть совокупности, которая является базой сравнения. За базу сравнения принимают наибольшее значение.

Относительная величина планового задания (ОВПЗ) используется для расчёта в процентном отношении увеличения (уменьшения) величины показателя плана по сравнению с его базовым уровнем в предшествующем периоде, для чего используется формула:

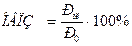, (2.9)

где Р_пл - плановый показатель;

Р₀ - фактический (базовый) показатель в предшествующем периоде.

Относительная величина выполнения плана (ОВВП) характеризует степень выполнения планового задания за отчётный период (%) и рассчитывается по формуле:

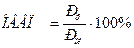, (2.10)

где Р_ф – фактическая величина выполнения плана за отчётный период;

Р_пл - величина плана за отчётный период.

Относительная величина динамики (ОВД) характеризует изменение объёма одного и того же явления во времени в зависимости от принятого базового уровня.

ОВД рассчитывают как отношение уровня анализируемого явления или процесса в текущий момент времени к уровню этого явления или процесса за прошедший период времени. В результате мы получаем коэффициент роста, который выражается кратным отношением. При исчислении этой величины в процентах (результат умножается на 100) получаем темп роста.

Темпы роста можно просчитывать как с постоянным базовым уровнем (базисные темпы роста - ОВД_б ), так и с переменным базовым уровнем (цепные темпы роста - ОВД_ц ):

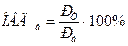, (2.11)

где Р_т - уровень текущий;

Р_б - уровень базисный;

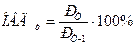, (2.12)

где Р_т - уровень текущий;

Р_т-1 - уровень, предшествующий текущему.

Относительная величина сравнения (ОВСр) - соотношение одноимённых абсолютных показателей, относящихся к разным объектам, но к одному и тому же времени (например, соотносятся темпы роста населения в разных странах за один и тот же период времени):

(2.13)

где М_А - показатель первого одноимённого исследуемого объекта;

М_Б - показатель второго одноимённого исследуемого объекта (база сравнения).

Все предыдущие показатели относительных величин характеризовали соотношения одноименных статистических объектов.

Однако есть группа относительных величин, которые характеризуют соотношение разноименных, но связанных между собой статистических показателей. Эту группу называют группой относительных величин интенсивности (ОВИ), которые выражаются, как правило, именованными числами.

В статистической практике относительные величины интенсивности применяются при исследовании степени объёмности явления по отношению к объёму среды, в которой происходит распространение этого явления. ОВИ здесь показывает, сколько единиц одной совокупности (числитель) приходится на одну, на десять, на сто единиц другой совокупности (знаменатель).

Примерами относительных величин интенсивности могут служить показатели уровня технического развития производства, уровня благосостояния граждан, показатели обеспеченности населения средствами массовой информации, предметами культурно-бытового назначения и т.д.

ОВИ рассчитывается по формуле:

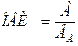, (2.14)

где А - распространение явления;

В_А - среда распространения явления А.

При расчёте относительных величин интенсивности может возникнуть проблема выбора адекватной явлению базы сравнения (среды распространения явления). Например, при определении показателя плотности населения нельзя брать в качестве базы сравнения общий размер территории того или иного государства, в этом случае базой сравнения может быть лишь территория в 1 км². Критерием правильности расчёта является сопоставимость по разработанной методологии расчёта сравниваемых показателей, применяющихся в статистической практике.

Вопросы для самоконтроля

1. Раскройте понятие и значимость абсолютных статистических величин. Приведите примеры абсолютных величин

2. В каких единицах измерения выражаются абсолютные статистические величины? Приведите примеры

3. Раскройте понятие и значимость относительных статистических величин

4. Каковы основные условия правильного расчёта относительной величины?

5. В какой форме могут быть выражены относительные величины?

6. Какие существуют виды относительных величин? Приведите примеры их расчёта