Задание для Задачи 1.

определить эквивалентное сопротивление цепи, токи в неразветвлённых участках и в ветвях цепи, напряжения на резисторах цепи. Составить баланс мощностей

Вариант 1

Дано: R₁=7 Ом; R₂=10 Ом; R₃=2 Ом; R₄=3 Ом, U = 120 В.

Вариант 2

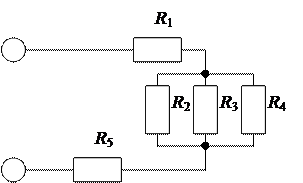
Дано: R₁=1 Ом; R₂=2 Ом; R₃=3 Ом; R₄=3 Ом; R₅=4 Ом, U = 120 В

Вариант 3

Дано: R₁=10 Ом; R₂=5 Ом; R₃=2 Ом; R₄=3 Ом, U = 120 В

Вариант 4

Дано: R₁=2 Ом; R₂=10 Ом; R₃=4 Ом; R₄=6 Ом; R₅=1 Ом, U = 120 В

Вариант 5

Дано: R₁=5 Ом; R₂=7 Ом; R₃=3 Ом; R₄=10 Ом, U = 120 В

Вариант 6

Дано: R₁=4 Ом; R₂=2 Ом; R₃=1 Ом; R₄=6 Ом; R₅=10 Ом; R₆=1 Ом; R₇=2 Ом, U = 120 В

Вариант 7

Дано: R₁=1 Ом; R₂=2 Ом; R₃=4 Ом; R₄=6 Ом; R₅=R₆=1 Ом; R₇=10 Ом, U = 120 В

Вариант 8

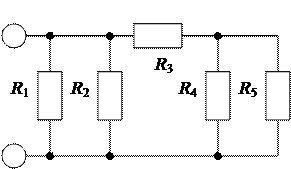
Дано: R₁=10 Ом; R₂=5 Ом; R₃=1 Ом; R₄=2 Ом; R₅=6 Ом, U = 120 В

Вариант 9

Дано: R₁=8 Ом; R₂=15 Ом; R₃=20 Ом; R₄=6 Ом, U = 120 В

Вариант 10

Дано: R₁=10 Ом; R₂=20 Ом; R₃=15 Ом; R₄=5 Ом; R₅=4 Ом, U = 120 В

2. Расчёт сложных цепей методом узловых и контурных уравнений

Пример расчёта методом узловых и контурных уравнений (по правилам Кирхгофа).

Задача. Рассчитать токи в цепи, представленной на рисунке, если Е₁ = 48 В, Е₂ = 36 В,

R₁ = 35 Ом, R₂ = 36 Ом, R₃ = 50 Ом. R₀₁ = 5 Ом, R₀₂ = 4 Ом,

Электрическая схема

Решение

1. Определяем количество ветвей цепи : три ветви.

2. Произвольно задаемся положительными направлениями токов в ветвях (указываем на схеме стрелками) и направлениями обходов в контурах ( по часовой стрелке).

3. Определяем количество уравнений, составленных по 1 и 2 правилам Кирхгофа (число уравнений равно числу неизвестных токов в цепи): m = 3 (три уравнения )

4. Определяем число независимых уравнений, составляемых по первому правилу Кирхгофа: (n −1) уравнений, где n − количество узлов в цепи (два); n −1 = 2 − 1 = 1.

5. Определяем число уравнений, составленных по второму правилу Кирхгофа : m − (n − 1) = 3 − (2 − 1) = 3 − 2 + 1 = 2 .

6. Составляем систему уравнений : 7. Подставляем числовые значения:

I₁ + I₂ = I₃ I₁ + I₂ = I₃

E₁ = I₁ (R₁ + R₀₁) + I₃ R₃ 48 = I₁ (35 + 5) + I₃∙ 50

E₁ − E₂ = I₁ (R₁ + R₀₁) − I₂ (R₂ + R₀₂) 48 − 36 = I₁ (35 + 5) − I₂ (36 + 4)

8. Приведем уравнения к нормальному виду : 9. Вторую и третью строку сократим :

I₁ + I₂ − I₃ = 0 I₁ + I₂ − I₃ = 0

40 I₁ + 50 I₃ = 48 20 I₁ + 25 I₃ = 24

40 I₁ − 40 I₂ = 12 10 I₁ − 10 I₂ = 3

10. Решаем данную систему способом подстановки ( можно решать различными способами) :

I₃ = I₁ + I₂ 20 I₁ + 25 I₁ + 25 I₂ = 24 45 I₁ + 25 I₂ = 24 │ 45 I₁ + 25 I₂ = 24

20 I₁ + 25 (I₁ + I₂) = 24 10 I₁ − 10 I₂ = 3 10 I₁ − 10 I₂ = 3 │2,5 + 25I₁ −25I₂ = 7,5

10 I₁ − 10 I₂ = 3

откуда 70 I₁ = 31,5 I₁ = 31,5 / 70 = 0,45 A; I₁ = 0,45 A

11. Подставим значение тока I₁ в уравнение 10 I₁ − 10 I₂ = 3 и определим ток второй ветви :

I₂ = (10 ∙ 0,45 −3) / 10 = 0,15 A ; I₂ = 0,15 A

12. Подставим значения токов I₁ и I₂ в уравнение I₁ + I₂ = I₃ , определим ток третьей ветви :

0,45 + 0,15 = I₃ ; I₃ = 0,6 А.

13. Поскольку все токи получились положительными, направления всех действительных токов совпадают с

направлениями токов предполагаемых.