Задача №2. В четырёхпроводную линию трёхфазной симметричной сети с фазным напряжением В включены три группы одинаковых ламп: 1) 30 ламп; 2) 25 ламп; 2) 20 ламп.

№4.12

В четырёхпроводную линию трёхфазной симметричной сети с фазным напряжением В включены три группы одинаковых ламп: 1) 30 ламп; 2) 25 ламп; 2) 20 ламп.

Сопротивление каждой лампы считать неизменным и равным 300 Ом.

Определить ток в нейтральном проводе. Под каким напряжением окажется каждая группа ламп при обрыве нейтрального провода в точке .

Дано: +25 ко всем показателям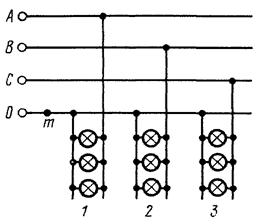

РЕШЕНИЕ

Так как лампы включены параллельно, тогда сопротивление каждой группы составит:

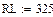
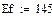
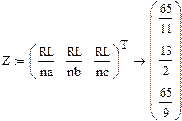
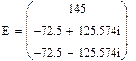
Рассчитаем смещение нейтральной точки при обрыве нейтрального провода методов двух узлов:

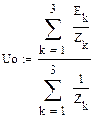
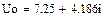
Далее вычислим напряжения на каждой группе как разницу напряжений фаз и напряжения в нейтральной точке (их комплексные и действительные значение):

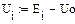
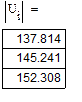
2.3. Задача №3

Определить токи в ветвях схемы рис. 1.методом контурных токов. Правильность решения проверить по балансу мощностей.

Рис. 1.

Решение

1. В соответствии с алгоритмом, зададимся направлением токов ветвей и обозначим их на схеме рис. 1.3.1.

2. Определяем независимые контура и выбираем направления контурных токов I_к1, I_к2, I_к3.

3. Поскольку в схеме имеется ветвь, содержащая источник тока J, контурный ток I_к3 = J, а для контурных токов I_к1 и I_к2запишем систему уравнений метода контурных токов:

{ I к1 ⋅ ( R 3 + R 6 )− I к2 ⋅ R 6 −J⋅ R 3 =− E 1 − E 6 I к2 ⋅ ( R 4 + R 5 + R 6 )− I к1 ⋅ R 6 −J⋅ R 4 = E 6

или

{      I к1 ⋅ ( R 3 + R 6 )− I к2 ⋅ R 6                              =− E 1 − E 6 +J⋅ R 3 − I к1 ⋅ R 6                  + I к2 ⋅ ( R 4 + R 5 + R 6 )= E 6 +J⋅ R 4

Подставив значения сопротивлений, получаем численную систему уравнений метода контурных токов с двумя неизвестными контурными токами:

{     25 I к1      −5 I к2 =−5    −5 I к1 +14 I к2 =40

откуда

I к1 =0,4  A;    I к2 =3  A.

4. Определяем токи в ветвях схемы по методу контурных токов:

I 1 = I к1 =0,4  A;    I 5 =− I к2 =−3  A;    I 6 = I к2 − I к1 =3−0,4=2,6  A.

Хотя все токи в ветвях можно определить методом контурных токов (I₃ = I_к3 – I_к1; I₄ = I_к3 – I_к2), токи I₃ и I₄ определим по первому закону Кирхгофа. Составим уравнения по первому закону Кирхгофа:

для узла a:

− I 5 −J+ I 4 =0,

откуда

I 4 = I 5 +J= ( −3 )+2=−1  A;

для узла b:

− I 1 − I 3 +J=0,

откуда

I 3 =J− I 1 =2−0,4=1,6  A.

5. Правильность решения проверяем по балансу мощностей. Предварительно находим напряжение на зажимах источника тока:

U ad = φ a − φ d =J⋅ R 2 + I 3 ⋅ R 3 + I 4 ⋅ R 4 − E 2 =    

      =2⋅10+1,6⋅20+ ( −1 )⋅5−10=37  B.  

  Тогда

    E 2 ⋅J+ U ad ⋅J+ E 1 ⋅ ( − I 1 )+ E 6 ⋅ I 6 = J 2 ⋅ R 2 + I 3 2 ⋅ R 3 + I 4 2 ⋅ R 4 + I 5 2 ⋅ R 5 + I 6 2 ⋅ R 6 ; 10⋅2+37⋅2+15⋅ ( −0,4)+30⋅2,6= 2 2 ⋅10+ 1,6 2 ⋅20+ ( −1 ) 2 ⋅5+ ( −3 ) 2 ⋅4+ 2,6 2 ⋅5;                                                                   166  Вт=166  Вт.