Задача №4. Рассчитать цепь рис. 2. методом узловых, потенциалов.

Рассчитать цепь рис. 2. методом узловых, потенциалов.

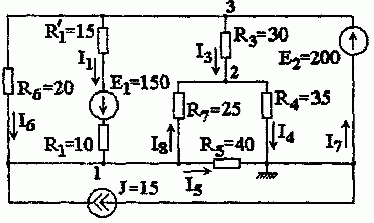
Рис. 2.

Решение. В рассматриваемой схеме четыре узла. Заземлим узел 4 (опорный узел)

φ 4 =0.

Тогда

φ 3 = φ 4 + E 2 =200  B.

Необходимо найти потенциалы узлов 1 и 2. Составим систему уравнений по методу узловых потенциалов для узлов 1 и 2.

Рассматривая узел 1, получим

φ 1 ⋅ g 11 − φ 2 ⋅ g 12 − φ 3 ⋅ g 13 =J+ E 1 R 1 + R ′ 1

или

φ 1 ⋅ g 11 − φ 2 ⋅ g 12 =J+ E 1 R 1 + R ′ 1 + E 1 ⋅ g 13 .

В правой части этого уравнения оба слагаемых учтены со знаком плюс, так как J и E1 направлены к узлу 1.

Рассматривая узел 2 (правая часть уравнения равна нулю, так как в ветвях, подсоединенных к узлу 2, нет источников энергии), получим

− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 − φ 3 ⋅ g 23 =0

или

− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 = E 2 ⋅ g 23 .

Найдем собственную проводимость первого узла

g 11 = 1 R 6 + 1 R 1 + R ′ 1 + 1 R ИТ + 1 R 2 + 1 R 5 = 1 20 + 1 25 + 1 25 + 1 40 =0,155  См.

Проводимость ветви с идеальным источником тока равна нулю, так как внутреннее сопротивление идеального источника тока RИТ равно бесконечности.

Собственная проводимость узла 2

g 22 = 1 R 2 + 1 R 3 + 1 R 4 = 1 25 + 1 30 + 1 35 =0,102  См.

Взаимные проводимости между узлами

g 13 = 1 R 6 + 1 R 1 + R ′ 1 = 1 20 + 1 25 =0,09  См; g 21 = g 12 = 1 R 2 = 1 25 =0,04  См; g 23 = 1 R 3 = 1 30 =0,033  См.

Подставив в уравнения известные величины, получим

{ φ 1 ⋅0,155− φ 2 ⋅0,04=39 − φ 1 ⋅0,04+ φ 2 ⋅0,102=6,6

Для решения этой системы используем метод определителей. Главный определитель системы

Δ=| 0,155 −0,04 −0,04 0,102 |=0,01421.

Частные определители

Δ 1 =| 39 −0,04 6,6 0,102 |=4,242; Δ 2 =| 0,155 39 −0,04 6,6 |=2,583.

Находим потенциалы узлов

φ 1 = Δ 1 Δ = 4,242 0,01421 =298,6   В;    φ 2 = Δ 2 Δ = 2,583 0,01421 =181,8   В.

Определяем токи в ветвях (положительные направления токов в ветвях с ЭДС выбираем по направлению ЭДС, в остальных ветвях произвольно)

I 1 = φ 3 − φ 1 + E 1 R 1 + R ′ 1 = 200−298,6+150 10+15 =2,056  А.

В числителе этого выражения от потенциала узла 3, из которого вытекает ток I1, вычитается потенциал узла 1, к которому ток подтекает. Если ЭДС ветви совпадает (не совпадает) с выбранным направлением тока, то она учитывается со знаком плюс (минус). В знаменателе выражения учитываются сопротивления ветви.

Аналогично определяем другие токи (направления токов указаны на схеме рис. 1.4.1)

I 1 = φ 3 − φ 1 R 6 = 200−298,6 20 =−4,93  А; I 2 = φ 1 − φ 2 R 2 = 298,6−181,8 25 =4,67  А; I 3 = φ 3 − φ 2 R 3 = 200−181,8 30 =0,607  А; I 4 = φ 2 − φ 4 R 4 = 181,8−0 35 =5,194  А.

Для определения тока в ветви с идеальной ЭДС зададимся направлением тока I7. По первому закону Кирхгофа для узла 3 составим уравнение

− I 7 + I 3 + I 1 + I 6 =0.

Откуда

I 7 = I 3 + I 1 + I 6 =0,607+2,056−4,98=−2,317  A.

Литература

1. Борисов Ю.М. Электротехника: учеб. пособие для вузов / Ю.М. Борисов, Д.Н. Липатов, Ю.Н. Зорин. – Изд.3-е, перераб. и доп.; Гриф МО. – Минск: Высш. шк. А, 2007. – 543 с

2. Григораш О.В. Электротехника и электроника: учеб. для вузов / О.В. Григораш, Г.А. Султанов, Д.А. Нормов. – Гриф УМО. – Ростов н/Д: Феникс, 2008. – 462 с

3. Лоторейчук Е.А. Теоретические основы электротехники: учеб. для студ. учреждений сред. проф. образования / Е.А. Лоторейчук. – Гриф МО. – М.: Форум: Инфра-М, 2008. – 316 с.

4. Федорченко А.А. Электротехника с основами электроники: учеб. для учащ. проф. училищ, лицеев и студ. колледжей / А.А. Федорченко, Ю.Г. Синдеев. – 2-е изд. – М.: Дашков и К°, 2010. – 415 с.

5. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей, учебное пособие для электротехнич., радиотехнич. Спец. Вузов – 1990. – 544 с.