
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткие теоретические сведения. В настоящей работе исследуются три электрические цепи переменного тока, состоящие из катушки индуктивности
В настоящей работе исследуются три электрические цепи переменного тока, состоящие из катушки индуктивности, батареи конденсаторов и их последовательного соединения. Реальная катушка индуктивности характеризуется активным сопротивлением RК и индуктивным сопротивлением
ХL = ω∙L, (11)
где ω – угловая частота переменного тока, рад/с,
L – индуктивность катушки, Гн (генри).
Заметим, что при исследовании идеальной катушки индуктивности ее активным сопротивлением пренебрегают и рассматривают идеальную катушку, как элемент, обладающий только индуктивным сопротивлением ХL.
Батарея конденсаторов характеризуется емкостным сопротивлением
ХС =  , (12)
, (12)
где C – емкость батареи, Ф .
И индуктивное и емкостное сопротивления являются реактивными сопротивлениями.
При последовательном соединении катушки и конденсатора (рис. 6) ток цепи определяется как
I = 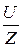 =
=  =
= 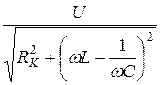 (13)
(13)
где Z - полное сопротивление цепи.
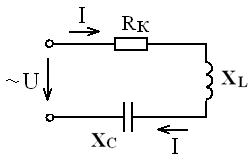
Рис.6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений (последовательная R-L-C цепь).
Формула (13) представляет собой выражение закона Ома для цепи переменного тока с последовательным соединением катушки и конденсатора.
В общем случае при наличии в цепи нескольких сопротивлений каждого типа (активных, индуктивных и емкостных) выражение закона Ома для последовательной цепи переменного тока примет вид
I = 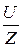 =
= 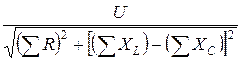
Напряжение на катушке
UK = I ∙ ZK =  (14)
(14)
где ZK – полное сопротивление катушки.
Напряжение на конденсаторе
UС = I ∙ ХС (15)
Активная мощность катушки
P = I 2 ∙ RK . (16)
Если в цепь переменного тока включить только катушку индуктивности с активным сопротивлением RK и индуктивным сопротивлением ХL, то ток в цепи определяется как
I = 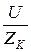 =
=  (17)
(17)
Известно, что в активном сопротивлении напряжение и ток совпадают по фазе, а в индуктивном напряжение опережает ток по фазе на 90º.
Векторная диаграмма для реальной катушки индуктивности представлена на рис.7, где φ – угол сдвига фаз между током и напряжением в катушке.
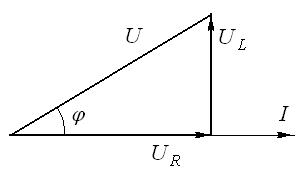
Рис.7. Векторная диаграмма электрической цепи с реальной катушкой индуктивности.
Разделив все стороны треугольника напряжений на величину тока I, получим треугольник сопротивлений (рис.8), а умножив на I2 – треугольник мощностей (рис.9), где Р, Q, S – активная, индуктивная (реактивная) и полная мощность катушки соответственно.

Рис.8. Треугольник сопротивлений для катушки индуктивности
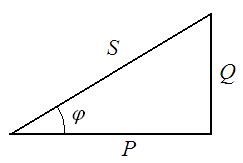
Рис.9. Треугольник мощностей для катушки индуктивности
Очевидно, что все три треугольника подобны, т.е. их углы равны между собой. Сos φ называется коэффициентом мощности цепи, т.к. его величина показывает, какая часть полной мощности S является активной.
cos φ = 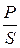 =
=  =
=  (18)
(18)
Таким образом, коэффициент мощности цепи может быть рассчитан как через мощности, так и через сопротивления или напряжения.
Расчет параметров катушки индуктивности при известных величинах I, U, P осуществляется следующим образом:
1) полное сопротивление из выражения (17) ZK = 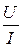 , Ом;
, Ом;
2) активное сопротивление из выражения (16) RK = 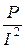 , Ом;
, Ом;
3) индуктивное сопротивление из треугольника сопротивлений XL = 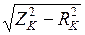 , Ом;
, Ом;
4) полная мощность, измеряемая в вольт-амперах S = U∙ I, ВА;
5) коэффициент мощности в соответствии с выражением (18)
cos φ =  ;
;
6) реактивная (индуктивная) мощность, изхмеряемая в вольт-амперах реактивных, из треугольника мощностей QL =  , ВАр;
, ВАр;
7) индуктивность катушки, измеряемая в генри, из выражения (9)
L =  , Гн (19)
, Гн (19)
где ω = 2πf, f – частота тока в сети, Гц.
Частота тока в сети f = 50 Гц, откуда ω = 2π50 = 314 рад/с.
Если в цепь переменного тока включить только конденсатор с емкостным сопротивлением ХС, то выражение закона Ома (13) примет вид
I = 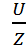 =
=  = U ω С (20)
= U ω С (20)
Известно, что в емкостном сопротивлении напряжение отстает от тока по фазе на 90º.
Векторная диаграмма для конденсатора представлена на рис.10.

Рис.10. Векторная диаграмма электрической цепи с конденсатором.
Из векторной диаграммы можно сделать следующие выводы. Активное сопротивление конденсатора RC = 0; активная мощность конденсатора Р=0. Полное сопротивление конденсатора равно его реактивному сопротивлению ZC = XC = 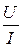 , а полная мощность – реактивной мощности S = QC = U∙ I. Коэффициент мощности cos φ = 0.
, а полная мощность – реактивной мощности S = QC = U∙ I. Коэффициент мощности cos φ = 0.
Емкость конденсатора определяется из выражения (12) C = 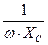 .
.
При последовательном включении катушки индуктивности и конденсаторной батареи получаем электрическую цепь с последовательным соединением активного RК, индуктивного XL и емкостного XC сопротивлений.
В такой цепи можно выделить три характерных режима работы в случаях, когда XL > XС , XL < XС , XL = XС . Векторные диаграммы для этих режимов представлены на рис.11. 1, 2 ,3 соответственно. Здесь UX – реактивное напряжение последовательной цепи.
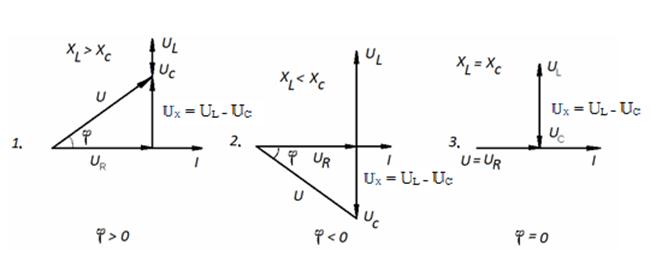
Рис.11. Векторные диаграммы цепи переменного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений при:
1) XL > XС; 2) XL < XС; 3) XL = XС.
Векторная диаграмма, представленная на рис.11.3, аналогична векторной диаграмме цепи переменного тока с активным сопротивлением в том смысле, что все напряжение, приложенное к зажимам цепи, падает на активном сопротивлении, т.е. U = UR, вектора напряжения U и тока I совпадают по фазе, угол сдвига между ними φ = 0 и коэффициент мощности цепи cos φ = 1.
Ток при этом будет иметь максимально возможного значения при данной величине приложенного напряжения.
Из выражения (13) при XL = XС
Imax = 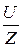 =
=  =
=  (21)
(21)
Отсутствие влияния реактивных сопротивлений на величину тока в цепи в этом случае объясняется тем, что при равенстве между собой XL и XС равные между собой и смещенные относительно друг друга по фазе на 180º напряжения UL и UС взаимно компенсируются.
Режим работы, устанавливающийся в цепи переменного тока с последовательным соединением R, XL и XС в случае XL = XС называется резонансом напряжений.
Сущность явления резонанса напряжений заключается в том, что напряжения, возникающие на зажимах катушки и на обкладках конденсатора могут в несколько раз превышать напряжение, приложенное к зажимам цепи.
Частота, при которой в цепи с заданными величинами L и С достигается резонанс напряжений, называется резонансной частотой (ωР, fР). Ее значение можно определить из условий резонанса ХL = ХС
ωРL = 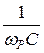 ; ωр =
; ωр = 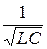 ; fР =
; fР = 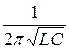 (22)
(22)
Резонанс напряжений может быть получен изменением угловой частоты переменного тока ω, индуктивности катушки L или емкости конденсаторной батареи С. В данной работе резонанс напряжений получают путем изменения величины емкости конденсаторной батареи.
При увеличении емкости конденсаторной батареи емкостное сопротивление цепи в соответствии с выражением (12) будет уменьшаться. Если подобрать значения индуктивности катушки L и начальной емкости конденсаторной батареи С0 таким образом, чтобы ХLбыло меньше, чем ХС0, то при увеличении емкости в соответствии с выражением (13) общее сопротивление цепи Z будет уменьшаться до того момента, когда ХС станет равным ХL, а затем начнет возрастать. При этом ток в цепи будет сначала увеличиваться, достигнет максимума при ХL = ХС, а затем начнет уменьшаться. Резонансу напряжений будет соответствовать значение емкости конденсаторной батареи СР, при котором ток I максимален (рис.12).
Определение параметров цепи переменного тока с последовательным соединением катушки и конденсатора осуществляется следующим образом.
При заданном значении напряжения U, приложенного к зажимам цепи и при каждом из заданных значений емкости конденсаторной батареи Сi измеряются величины тока I, напряжения UK, приложенного к катушке, напряжения UC, приложенного к конденсатору и активной мощности цепи Р. Остальные параметры цепи являются расчетными величинами.
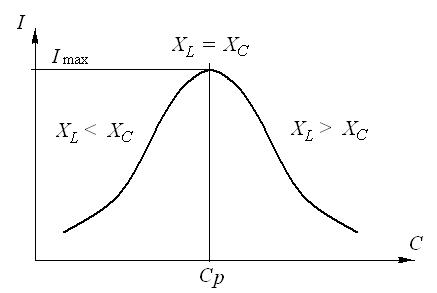
Рис.12. К определению резонансной емкости конденсаторной батареи при резонансе напряжений
Активное сопротивление катушки RK =  , Вт.
, Вт.
Полное сопротивление катушки ZK = 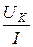 , Ом.
, Ом.
Индуктивное сопротивление катушки ХL =  , Ом.
, Ом.
Сопротивление катушки в процессе проведения лабораторной работы не изменяется, поэтому величины RК, ZК, и ХL достаточно вычислить один раз.
Емкостное сопротивление конденсатора ХС = 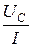 , Ом.
, Ом.
Реактивная (индуктивная) мощность катушки QL = I 2 ∙ ХL, ВАр.
Реактивная (емкостная) мощность конденсатора QС = I 2 ∙ ХС, ВАр.
Реактивная мощность цепи Q = QL - QС, ВАр.
Полная мощность цепи S = I ∙ U = 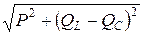 =
= 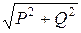 , ВА.
, ВА.
Коэффициент мощности цепи cos φ = 
Угол сдвига фаз между током и напряжением φ = arсcos  ,
,
Падение напряжения на активном сопротивлении катушки UR = I ∙ RK, В.
Падение напряжения на индуктивном сопротивлении катушки UL = I ∙ XL, В.
Активная мощность в цепи измеряется ваттметром. Ваттметр имеет две измерительные обмотки: токовую обмотку и обмотку напряжения. Фактически ваттметр измеряет значения тока, протекающего через токовую обмотку и значение напряжения, приложенного к активным сопротивлениям, расположенным между зажимами обмотки напряжения, и затем вычисляет значения активной мощности в соответствии с выражением Р = I UR.
План лабораторной работы
Задание 1. Определить электрические параметры катушки и конденсатора в цепи переменного синусоидального тока частотой f = 50 Гц.
1. Собрать электрическую схему c катушкой индуктивности (рис.13). Включая ваттметр, необходимо генераторные зажимы токовой обмотки и обмотки напряжения, отмеченные звездочками, присоединить к одному и тому же проводу со стороны источника электрической энергии (генератора).
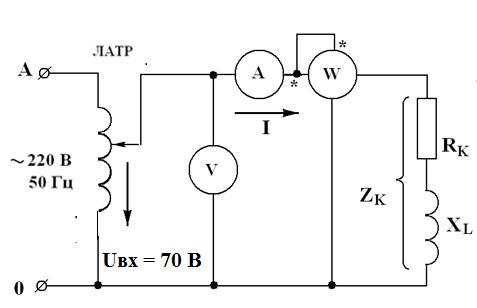
Рис.13. Схема исследования цепи переменного тока с катушкой индуктивности и с конденсатором: ЛАТР – лабораторный автотрансформатор (ЛАТР); V - вольтметр 75-150-300-600 В; A – амперметр 1-2 А; W – ваттметр U = 75-150-300-600 В, I = 1-2 A.
2. Установить напряжение, подаваемое на катушку UВХ = 70 В, с помощью ЛАТРа.
3. Измерить ток в цепи I и активную мощность Р.
4. Заменив катушку конденсатором, повторить пп.2 и 3.
5. Рассчитать параметры катушки индуктивности и конденсатора, указанные в табл.4.
6. Результаты измерений и вычислений внести в табл. 4.
7. Построить векторные диаграммы для цепей переменного тока с катушкой индуктивности и с конденсатором.
Задание 2. Получение резонанса напряжений в цепи переменного тока с последовательным соединением катушки и конденсатора.
1. Собрать электрическую схему (рис.14), используя приборы перечисленные в задании 1. Для измерения напряжений катушки UK и конденсатора UС использовать вольтметр V1 со свободными концами.

Рис.14. Схема исследования цепи переменного тока с последовательным соединением катушки и конденсатора.
2. Установить напряжение на входе исследуемой электрической схемы Uвх = 20 В с помощью ЛАТРа.
3. Измерить токи I, активные мощности P, напряжения на катушке UК и конденсаторе UC , изменяя емкость батареи конденсаторов (установленной на стенде) от 12 до 32 мкФ в следующем порядке: 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32 мкФ,
4. Рассчитать параметры последовательной цепи переменного тока, указанные в табл.5.
5. Результаты измерений и вычислений внести в табл. 5.
6. Построить графики зависимостей тока в цепи I, напряжений на катушке UК и конденсаторе UC, активной мощности цепи Р, а также коэффициента мощности cos φ от емкости конденсаторной батареи.
7. Построить векторные диаграммы цепи переменного тока, соответствующие значениям емкости С = 16 мкФ, С = 26 мкФ и С = СР (резонанс напряжений).
Содержание отчета
1. Электрические схемы с обозначениями приборов.
2. Расчет параметров последовательных цепей переменного тока.
3. Таблицы измеренных и вычисленных величин.
4. Графики зависимостей I(C), UK(C), UC(C), Р(C), cos φ(C).
5. Векторные диаграммы.
Контрольные вопросы
1. Как обозначается реальная катушка индуктивности и конденсатор на электрической схеме?
2. Можно ли измерить активное и индуктивное напряжения, падающие на катушке?
3. Что покажет ваттметр, установленный в цепи переменного тока с конденсатором?
4. Что необходимо знать для вычисления индуктивности катушки и емкости конденсатора, если известны их индуктивное и емкостное сопротивления?
5. Как изменятся активное и индуктивное сопротивления катушки при изменении частоты питающего тока?
6. Как изменяется сопротивление конденсатора при увеличении его емкости?
7. Почему косинус угла сдвига фаз между напряжением и током называется коэффициентом мощности?
8. Можно ли вычислить коэффициент мощности по треугольнику сопротивлений?
9. Чему равно активное сопротивление конденсатора?
10. Чему равен коэффициент мощности в схеме с конденсатором?
11. Какое условие должно выполняться в схеме с последовательным соединением R, ХL и ХC для получения резонанса напряжений?
12. Чему равен коэффициент мощности цепи при резонансе напряжений?
13. Почему явление в последовательной цепи переменного тока, когда ее полное сопротивление минимально, называется резонансом напряжений?
14. Какими способами можно получить резонанс напряжений в последовательной цепи переменного тока?
15. Какую мощность измеряет ваттметр?
16. При каком условии все напряжение, приложенное к зажимам последовательной RLC-цепи будет падать на активном сопротивлении?
17. Как и почему изменяется активная мощность в последовательной RLC-цепи при изменении емкости конденсатора?
18. Может ли в последовательной RLC-цепи протекать один и тот же ток при различных значениях емкости конденсатора?
19. Как изменится ток в последовательной RLC-цепи при переключении ее с переменного напряжения на постоянное той же величины?
20. В каких единицах измеряются активная, реактивная и полная мощность цепи переменного тока?
Таблица 4
| Элементы цепи | Измеренные величины | Вычисленные величины | |||||||||
| U | I | P | Zк | cos φ | S | Q | R | X | L | C | |
| В | А | Вт | Ом | – | ВА | ВАр | Ом | Ом | Гн | мкФ | |
| Катушка | 0,42 | 9,3 | |||||||||
| Конденсатор | 0,70 |
Таблица 5
| Измеренные величины | Вычисленные величины | |||||||||||||||||
| № опыта | C | I | Uк | Uc | P | Rк | XL | Zк | Xc | QL | QC | Q | S | cos φ | φ | UR | UL | |
| мкФ | А | В | В | Вт | Ом | Ом | Ом | Ом | ВАр | ВАр | ВАр | ВА | – | град | В | В | ||
| 0,17 | 28,5 | 45,1 | 1,52 | |||||||||||||||
| 0,23 | 38,6 | 52,3 | 2,82 | |||||||||||||||
| 0,30 | 51,1 | 59,7 | 4,77 | |||||||||||||||
| 0,36 | 60,4 | 63,7 | 6,79 | |||||||||||||||
| 0,38 | 63,8 | 60,5 | 7,60 | |||||||||||||||
| 0,36 | 60,4 | 52,8 | 7,02 | |||||||||||||||
| 0,34 | 56,5 | 44,7 | 6,02 | |||||||||||||||
| 0,31 | 52,0 | 38,0 | 5,09 | |||||||||||||||
| 0,29 | 48,7 | 33,0 | 4,40 | |||||||||||||||
| 0,27 | 45,3 | 28,7 | 3,76 | |||||||||||||||
| 0,25 | 42,0 | 24,9 | 3,31 | |||||||||||||||
Дата добавления: 2015-04-16; просмотров: 512; Мы поможем в написании вашей работы!; Нарушение авторских прав |