Метод эквивалентных преобразований

Для расчета простых электрических цепей с одним источником часто используется метод эквивалентных преобразований. Суть метода заключается в том, что отдельные участки схемы с последовательно или параллельно соединенными элементами заменяют одним эквивалентным элементом. Постепенным преобразованием участков схему упрощают и приводят к простей простейшей схеме состоящей из источника и одного эквивалентного элемента. Пример расчета схемы методом эквивалентного преобразования приведен на рисунке 2.5.

Рисунок 2.5 - Пример расчета схемы методом

эквивалентных преобразований

Встречаются схемы со сложным соединением элементов, которые нельзя отнести ни к последовательному, ни к параллельному соединению. Рассмотрим одну из таких схем, когда часть ее образует треугольник, вершинами которого являются три узла, а сторонами три сопротивления, включенные между этими узлами (рисунок 2.6 а). Для упрощения подобных схем во многих случаях бывает удобно заменить треугольник эквивалентной трехлучевой звездой (рисунок 2.6 б). В этом случае эквивалентные сопротивления звезды находятся по формулам:

, , .

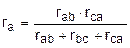При замене трехлучевой звезды эквивалентным треугольником сопротивление резисторов треугольника можно определить по формулам:

, , .

Рисунок 2.6 – Схемы соединения нагрузок

На рисунке 2.7 показана схема, для которой переход от звезды резисторов , , 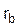к эквивалентному треугольнику, позволяет получить цепь с простым смешанным соединением и использовать метод эквивалентных преобразований для расчета схемы.

Рисунок 2.7 - Замена звезды эквивалентным треугольником