Расчет электрических цепей с помощью законов Кирхгофа

Для анализа разветвленных электрических цепей в электротехнике применяются законы Кирхгофа, выражающие два основных свойства электрических цепей. Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю:

.

При этом токи, направленные к узлу берут с одним произвольным знаком, а направленные от узла с противоположным.

По второму закону Кирхгофа алгебраическая сумма напряжений на участках (резистивных элементах) замкнутого контура равна алгебраической сумме ЭДС:

,

где m – число источников ЭДС в контуре, n – число резистивных элементов в контуре.

При этом напряжения, положительные направления которых совпадают с направлением обхода, берут с положительными знаками, а напряжения, положительные направления которых противоположны направлению обхода – с отрицательными знаками.

Для примера рассмотрим электрическую схему на рисунке 2.8. На схеме имеются три ветви (между точками 1-3, 4-7, 8-9), три независимых контура (1-8-9-3-2-1, 1-4-5-6-7-3-2-1, 4-8-9-7-6-5-4), два узла (4, 7).

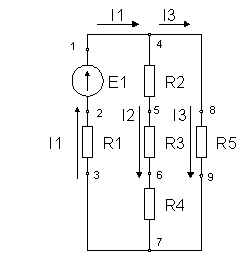
Рисунок 2.8 - Пример применения

законов Кирхгофа

Запишем уравнение, реализующее первый закон Кирхгофа для узла 4:

.

Уравнение, реализующее второй закон Кирхгофа для контура 1-8-9-3-2-1:

.

Для контура 1-4-5-6-7-3-2-1 уравнение по второму закону Кирхгофа:

.

Для нахождения токов в схеме необходимо составить систему из m уравнений, где m – число неизвестных токов, равное числу ветвей схемы. Порядок расчета электрических схем с помощью законов Кирхгофа должен быть следующий:

· Обозначить условно положительные направления токов на схеме.

· Составить (n – 1) – уравнений по первому закону Кирхгофа, где n – число узлов в схеме.

· Так как число неизвестных токов в схеме равно числу ее ветвей, а число ветвей всегда больше числа узлов, то недостающие уравнения составляют по второму закону Кирхгофа.

С помощью законов Кирхгофа можно рассчитывать цепи любой сложности, однако для сложных схем с несколькими источниками система уравнений получается слишком громоздкой. Для расчета таких схем применяют другие методы расчета.