Математические модели детерминированных радиотехнических сигналов

Глава 2. Детерминированные радиотехнические сигналы

Математические модели детерминированных радиотехнических сигналов

Детерминированные сигналы задаются аналитически и их параметры можно определить в любой момент времени.

К детерминированным сигналам относятся:

- Гармоническое колебание (рис 2.1) (колебание, изменяющееся по закону косинуса или синуса), описывается следующими выражениями:

(2.1)

где А₀, f₀, w₀, j₀ – постоянные величины, которые могут исполнять роль информационных параметров сигнала: А₀ – амплитуда, наибольшее отклонение какой-либо величины от положения равновесия или состояния покоя; f₀ – циклическая частота (имеет размерность в Гц); 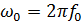- угловая частота (имеет размерность рад/с); j₀ – начальная фаза или начальный угол отклонения. Период одного колебания .

Путем воздействия на тот или иной параметр несущего колебания (2.1) можно получить требуемый вид модуляции (манипуляции), т.е. воздействуя на амплитуду – мы получаем амплитудную модуляцию (АМ), на частоту – частотную (ЧМ), на фазу – соответственно фазовую (ФМ).

Если амплитуда и фаза сигнала изменяются существенно медленнее, чем несущая частота 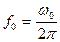, то полоса спектра такого сигнала 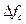много меньше и сигнал называется узкополосным.

Если амплитуда и фаза меняются с частотой соизмеримой или большей, чем , то это широкополосный сигнал.

- Прямоугольные видеоимпульсы (рис.2.2,а)

(2.2)

- Прямоугольные радиоимпульсы (рис.2.2,б)

(2.3)

Рис.2.2

- Треугольные видео (или радио) импульсы (соответственно рис.2.2,а и рис.2.3,б)

Рис.2.3

- Последовательность отсчетов, тестовые сигналы и т.д.