Простые и сложные сигналы.

Простые сигналы. Простой сигнал – это одиночный импульс или последовательность импульсов, вида (2.2).

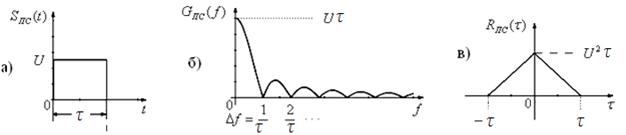
Рис.2.6

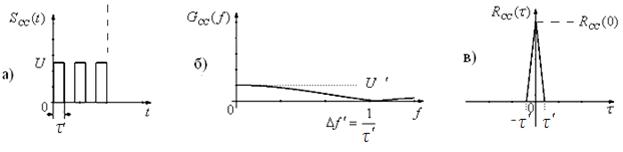
Рис. 2.7

Для одиночного импульса мы будем иметь сплошной спектр (рис. 2.6,б), запись которого имеет вид

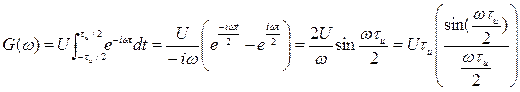
Для последовательности импульсов, или другими словами пачки импульсов - спектр будет иметь дискретный вид.

Размерность спектра (спектральной плотности) импульса будет определяться следующим образом .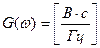

Полоса частот (рис. 2.6,б), где заключено 90% энергии сигнала равна:

.

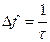Корреляционная функция простого сигнал (рис. 2,6,в) лежит в пределах от -t¢ до t¢ . Корреляционная функция – это энергия сигнала с размерностью 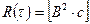и выражением вида

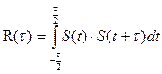
Чем уже корреляционная функция, тем легче, например, в радиолокации осуществить разрешение сигналов и определить параметры до цели по дальности, углу прихода, скорости движения объекта и т.д. Необходимо иметь как можно более острые КФ особенно при близко расположенных целях. Для заострения и укорачивания КФ казалось бы можно брать более короткие сигналы. Однако, энергия сигнала равна 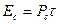, а это значит, что при уменьшении длительности τ уменьшается энергия сигнала. Следовательно уменьшается дальность обнаружения и соотношение сигнал/шум в точке приема, т.е помехоустойчивость.

База простого сигнала равна .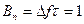

Сложные сигналы. Задача сложных сигналов, при той же исходной длительности сигнала τ сформировать узкую КФ, не снижая энергии сигнала. Информационный импульс длительностью τ разбивают на ряд импульсов одинаковой или разной длительностью (рис. 2.7,а).

Теперь ширина спектра (рис. 2.7,б) такого сигнала будет определяться самым коротким импульсом t¢, а корреляционная функция (рис. 2.7,в) будет лежать в пределах от -t¢ до t¢ .

Полоса частот, где заключено 90% сигнала равна (рис. 2.7,б):

. ()

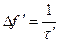Поскольку энергия по отношению к простому сигналу не изменилась то корреляционная функция (рис. 2.7,в), для сохранения своей площади по отношению к простому сигналу будет лежать выше сложного сигнала.

В свою очередь База сложного сигнала будет равна

. ()

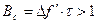В большинстве случаев большой интерес представляют сигналы с Базой сигнала равной

. ()

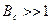Выражение () определяет собой широкополосный шумоподобный сигнал (ШШС). У такого сигнала структура его приближается к белому шуму, а корреляционная функция стремиться к дельта функции, т.е стремиться в бесконечность.

В качестве сложных сигналов могут выступать коды Баркера и сигналы линейной частотной модуляции (ЛЧМ).

Линейные частотно-модулированные сигналы (ЛЧМ).Исходный сигнал остается той же длительности, но внутри него происходит линейное нарастание частоты с девиацией 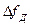(рис.2.8). Этот ЛЧМ сигнал уже сложный 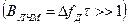. Длительность сигнала τ=const, следовательно, его энергия остается постоянной. Изменяя 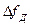, можно варьировать базой и сделать ее такой большой, что спектр сигнала будет близок к спектру белого шума, а его КФ будет стремиться к 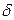- функции.

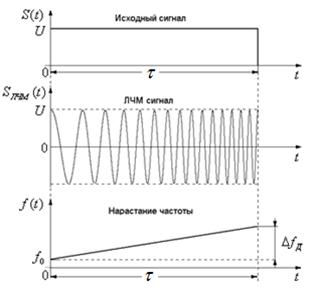Рис.2.8

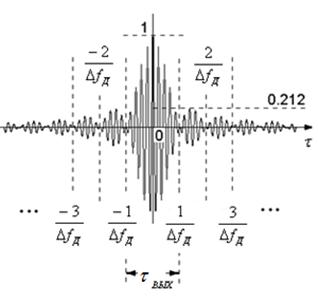Рис.2.9

Линейный частотно-модулированный сигнал можно представить в виде

,

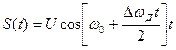(2.8)

где .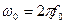

Ширина КФ определяется величиной 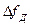(рис.2.9).

Прием ЛЧМ сигналов осуществляется на согласованный фильтр (СФ), на выходе которого имеется решающее устройство (РУ) (рис.2.10).

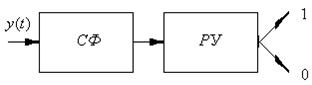
Рис.2.10

Согласованный фильтр представляет собой дисперсионную линию задержки с отводами на общий сумматор. Причем, учитывая разную скорость распространения различных гармонических колебаний, задержки отводов СФ выбраны так, чтобы по окончании импульса ЛЧМ все сигналы (гармоники) сложились бы одновременно в фазе. Это называется балансом фаз.

В результате такого одновременного сложения гармоник происходит сжатие сигнала. Коэффициентом сжатия находиться из выражения

,

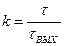(2.9)

где τ – длительность передаваемого сигнала;

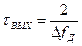- длительность сигнала на выходе СФ, которая обратно пропорциональна девиации частоты .

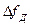Чем больше коэффициент сжатия, тем уже пик КФ и тем выше разрешающая способность и помехоустойчивость системы. Кроме того, при большой базе можно увеличивать длительность сигнала и тем самым повышать его энергию, т.к. 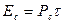. Недостатком ЛЧМ сигналов является достаточно большой уровень боковых лепестков КФ.

Сигналы Баркера.Баркер предложил коды, которые обладают таким свойством, что боковые лепестки КФ уменьшаются по закону 1/n, где n - значность кода. Правда, исследования показали, что значность кода может быть только такой:n = 2, 3, 4, 5, 7, 11, 13.

Код Баркера состоит из определенного количества импульсов равной длительности. При этом, чем больше элементов n, тем короче импульс 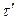, тем шире спектр, а, значит, и уже КФ. Далее осуществляют фазовое кодирование, при котором осуществляется скачок фазы при переходе от 1 к 0 и обратно на 180⁰ . При любом значении n распределение единиц и нулей может быть произвольным (рис.2.11). На рис.2.12 приведена КФ для n = 3,7,13.

Основание КФ прямоугольного импульса длительностью 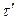в 2 раза больше, т.к. эта КФ представляет собой равнобедренный треугольник с основанием 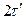. База сигналов, построенных по коду Баркера равна , а ширина спектра .

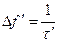Рис.2.11

Если принять величину центрального пика КФ R(0)=1, то для выбранного значения n уровень боковых лепестков будет в n раз меньше (рис.2.12).

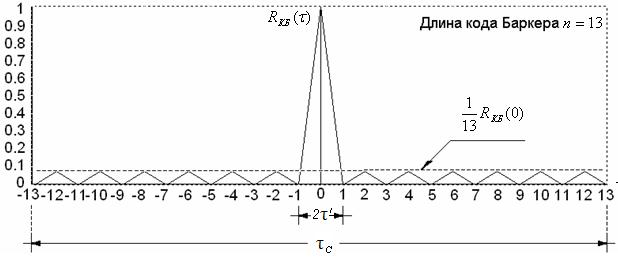
Рис.2.12

Прием сигналов Баркера осуществляется на СФ в виде дисперсионной линии задержки. Здесь так же сигналы складываются в фазе с приходом последней гармонической составляющей. В результате происходит сжатие принимаемого сигнала, энергия его возрастает в n раз в пределах сжатого сигнала, а боковые лепестки в n раз уменьшаются.

Коды Баркера позволяют не только увеличить разрешающую способность, но и увеличить помехоустойчивость и скрытность передачи, т.к. сигнал по своей структуре близок к ШШС.

Выводы: переход от простых к сложным сигналам позволяют обострить корреляционную функцию 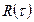, а это значит, что можно существенно улучшить различение, разрешение и распознавания цели.

Рис. 2.13

Как видно из рис. 2.13 зондирующий сигнал надо брать с острыми корреляционными функциями 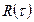(сложные сигналы), так как легче произвести различие, разрешение, измерение и т.д.

Вот почему выгоднее брать сигналы не простые, а сложные.