Метод эквивалентного генератора. В основе этого метода лежит теорема об эквивалентном генераторе

В основе этого метода лежит теорема об эквивалентном генераторе. В соответствии с теоремой об эквивалентном генераторе, любая линейная цепь относительно выбранной ветви может быть представлена эквивалентным источником ЭДС (или эквивалентным источником тока 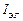) с эквивалентным внутренним сопротивлением 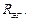Получаются два метода: метод эквивалентного источника (генератора) ЭДС и метод эквивалентного источника (генератора) тока.

ЭДС генератора Е_ЭГ численно равна напряжению, возникающему на зажимах выбранной ветви, если ее сопротивление положить равным бесконечности (так называемый холостой ход генератора). Сопротивление генератора R_ЭГ равно входному сопротивлению схемы R_ВХ относительно зажимов выбранной ветви (при расчете входного сопротивления величину ЭДС источника ЭДС и величину тока источника тока полагают равными нулю, а в схеме остаются внутренние сопротивления источников, которые для идеального источника ЭДС R_ВН = 0, а идеального источника тока R_ВН = ∞). Ток источника (генератора) тока 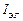численно равен току, протекающему через проводник, соединяющий клеммы, к которым была подключена ветвь с искомым током (режим короткого замыкания).

а б

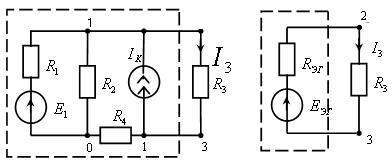
Рис. 3.4. Исходная (а) и вспомогательная (б) схемы для метода эквивалентного генератора

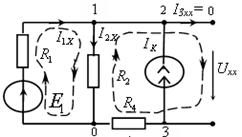
В качестве примера рассмотрим схему рис 3.4 для метода эквивалентного источника ЭДС, где определим ток в ветви с сопротивлением R₃. Для расчета тока выделим эту ветвь (рис. 3.5, а) и определим параметры эквивалентного генератора Е_ЭГ и R_ЭГ (рис. 3.5, б).

а б
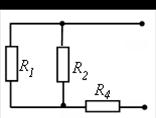
Рис. 3.5. Участки цепи для расчета методом эквивалентного генератора

ЭДС эквивалентного генератора можно определить по законам Кирхгофа для схемы рис. 3.5, а, как Е_ЭГ = U_ХХ. Определим напряжение U_ХХ:

.

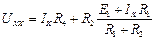Сопротивление эквивалентного генератора можно определить как входное сопротивление 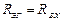по схеме рис. 3.5, б:

.

Тогда ток определим из выражения второго закона Кирхгофа для схемы рис. 3.4, б: