
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Параллельное соединение индуктивно связанных элементов
Пусть две индуктивно связанные катушки с параметрами  и M соединены параллельно (рис. 3.5). Оба вида соединения будем рассматривать одновременно. Согласное соединение получается при подключении к одному и тому же узлу одноименных зажимов, встречное разноименных.
Первый случай отмечен на схеме звездочками, второй точками. Запишем уравнения Кирхгофа для рассматриваемой цепи и решая их, получим выражения, определяющие токи: и M соединены параллельно (рис. 3.5). Оба вида соединения будем рассматривать одновременно. Согласное соединение получается при подключении к одному и тому же узлу одноименных зажимов, встречное разноименных.
Первый случай отмечен на схеме звездочками, второй точками. Запишем уравнения Кирхгофа для рассматриваемой цепи и решая их, получим выражения, определяющие токи:
|  Рис. 3.5. Параллельное соединение индуктивно связанных элементов
Рис. 3.5. Параллельное соединение индуктивно связанных элементов
|


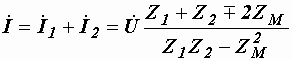 .
.
В этих уравнениях 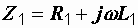 ,
,  ,
,  .
.
Входное комплексное сопротивление цепи равно отношению напряжения к току на ее зажимах:
 .
.
При отсутствии магнитной связи между катушками, полагая  , получаем известную формулу для определения общего сопротивления двух параллельных ветвей:
, получаем известную формулу для определения общего сопротивления двух параллельных ветвей:
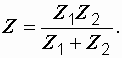
Во всех приведенных выражениях у слагаемых с двойным знаком верхний знакотносится к согласному соединению, нижний к встречному.
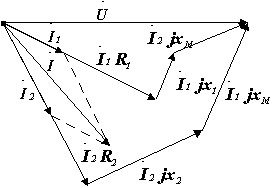
На рис. 3.6 представлены векторные диаграммы рассматриваемой цепи при согласном (а) и встречном (б) соединениях катушек. При построении векторы 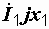 и
и  проводятся перпендикулярно току
проводятся перпендикулярно току  , а векторы
, а векторы  и
и  перпендикулярно току
перпендикулярно току  . При согласном соединении напряжения взаимной индукции опережают соответствующие токи, при встречном отстают от них.
. При согласном соединении напряжения взаимной индукции опережают соответствующие токи, при встречном отстают от них.
а)
| б)

|
Рис. 3.6. Векторные диаграммы для параллельного соединения индуктивно связанных элементов
Дата добавления: 2015-04-16; просмотров: 293; Мы поможем в написании вашей работы!; Нарушение авторских прав |