Производственная функция. Способы минимизации издержек и максимизации прибыли

Производство представляет собой процесс соединения факторов производства с целью получения новых благ и услуг, необходимых потребителям. Экономическая деятельность фирмы может быть описана производственной функцией: Q = f(F₁, F₂, … F_n), где Q – максимальный объём производства; F₁, F₂, … F_n – количество используемых факторов производства. Если известен результат (Q), который необходимо достичь, минимизируются ресурсы (F). Если известны ресурсы, максимизируется результат.

Производственная функция указывает на существование альтернативных возможностей, при которых различные сочетания факторов производства, обеспечивают один и тот же объём продукции. Если возможны различные сочетания факторов производства, значит, есть вариант, при котором можно добиться их оптимального сочетания. Достижению оптимального сочетания факторов производства способствует выполнение двух правил: правило минимизации издержек
и правило максимизации прибыли.

1. Правило минимизации издержек. Согласно этому правилу, минимизация издержек (соответственно максимизация выпуска на единицу затрат) обеспечивается тогда, когда последний рубль, затраченный на каждый ресурс, даёт одинаковый предельный продукт,
т.е.МР₁/Р₁ = МР₂/Р₂ = … = МР_n/Р_n, где n – количество применяемых ресурсов.

Однако минимизации издержек недостаточно для максимизации прибыли. Существуют различные объёмы выпуска, при которых фирма может минимизировать издержки. Однако имеется только один объём выпуска продукта, при котором максимизируется прибыль.

2. Правило максимизации прибыли. Выпуск продукта с максимальной прибылью осуществляется, как известно, при МR = MC. Применительно к использованию ресурсов это правило формулируется следующим образом: количество применяемого ресурса, обеспечивающее максимальную прибыль, должно быть таким, чтобы цена
ресурса была бы равна его предельной доходности, т.е. Р = МRР или МRР/Р = 1.

Таким образом, миксимизирующее прибыль использование экономических ресурсов на совершенных конкурентных рынках предполагает такую их оптимальную комбинацию, при которой каждый вводимый ресурс применяется до тех пор, пока его предельная доходность не станет равной его цене или: МRР₁/Р₁ =МRР₂/Р₂ = … =
= МRР_n/Р_n = 1.

В условиях, когда фирма влияет на уровень цен, формула имеет следующий вид: МRP₁/MRC₁ = MRP₂/MRC₂ = … =MRP_n/MRC_n = 1.

Минимальное количество используемых ресурсов можно определить, применяя ординалистский инструментарий, графическое совмещение двух типов кривых: изоквант и изокосты.

Изокванта – геометрическое место точек, отражающих комбинации факторов производства (например, труда–L и капитала–K), обеспечивающие одинаковый выпуск продукта. Можно изобразить серию изоквант, или карту изоквант – это их совокупность, представляющая собой разный объём выпуска. Свойства изоквант совпадают со свойствами кривых безразличия. Наклон изокванты характеризуется предельной нормой технологического замещения факторов производства (MRTS_LK), определяемой компенсирующим количеством одного фактора (DК), которое должно уменьшится при увеличении количества другого фактора (DL) для сохранения постоянного уровня выпуска продукта. MRTS_LK = – DK/DL.

Изокоста – бюджетная линия производителя, геометрическое место точек, отражающих именно доступные для него комбинации факторов производства при неизменных ценах и доходе (см. рис. 12.5.). Свойства изокост: 1) расположение изокосты зависит от величины капитала производителя и от цен на ресурсы; 2) наклон изокосты равен P_L/P_K, где P_L и P_K – цена соответственно труда и капитала.

Равновесие производителя (и, соответственно, максимизация выпуска продукции с минимальными затратами) достигается в точке
касания изокосты с ближайшей изоквантой (в точке Е), с которой она имеет одинаковый наклон. MRTS_LK = P_L/P_K. ( рис. 12.5.).

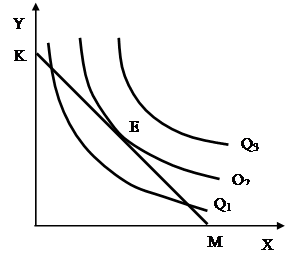Рис. 12.5. Определение

точки равновесия (Е)

производителя

Q₁, Q₂, Q₃ – изокванты;

КМ – изокоста.

Данная выше интерпретация теории предельной производительности, согласно которой ресурсы получают вознаграждение в соответствии с их предельной производительностью (доходностью), предполагает, что на каждую единицу ресурса приходится доход, совпадающий с его вкладом в процесс производства. Максимальная прибыль фирмами–покупателями ресурсов извлекается при таком объёме использования ресурсов, когда их предельная доходность (МRР) становится равной их цене (Р). Поэтому каждый хозяйствующий субъект получает доход согласно этому вкладу, что даёт основание говорить
о гармонии экономических интересов.

Однако эта теория подвергается критике, поскольку: во–первых, существует неравенство в распределении ресурсов, закрепляемое собственностью, передаваемой по наследству; во–вторых, при несовершенной конкуренции цены на ресурсы не отражают их вклада в производство.

Контрольные вопросы

1. Каковы особенности спроса на ресурс?

2. Почему кривая спроса на ресурс в условиях совершенной
конкуренции является более эластичной, чем кривая спроса на ресурс со стороны монополии?

3. Объясните правило MRP = MRC.

4. Как определяется цена на ресурс на конкурентном рынке?

5. Как определяется цена на ресурс на монопсоническом рынке?

5. Что описывает производственная функция?

6. Объясните правило минимизации издержек.

7. Объясните правило максимизации издержек.

8. Покажите равновесие производителя, используя изокванты
и изокосты.

9. Каковы свойства изоквант и изокост?

10. Почему распределение продукта в условиях совершенной
конкуренции является справедливым?