
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Общие сведения. 1.1. Анализ погрешностей, возникающих при обработке деталей резанием
1.1. Анализ погрешностей, возникающих при обработке деталей резанием
Отклонение от размера является важнейшим показателем качества всего изделия. Оценка качества путем определения фактических размеров занимает в технологии машиностроения ведущее место. В случае изготовления единичной детали или изделия размер и допустимые отклонения определяют непосредственным измерением. При изготовлении изделий сравнительно большими партиями на предварительно настроенных станках измерение каждой детали, тем более по многим параметрам, не представляется возможным. Для анализа точности в этом случае используют аппарат математической статистики.
Аппарат математической статистики может быть применен, если иметь дело с массовым явлением. Процент положительных результатов в данной массовой операции называют вероятностью. В этих случаях всегда наблюдается рассеяние параметров. Так, обработка на предварительно настроенном станке партии заготовок в автоматическом режиме, т.е. без участия рабочего в каждом цикле работы станка, обязательно приведет к рассеянию размеров. Это объясняется одновременным воздействием на технологическую систему большого количества факторов.
Погрешности разделяют на случайные, систематические, но закономерно изменяющиеся и постоянные. Случайные погрешности возникают при изготовлении конкретной детали в результате каждый раз особой компоновки большого числа факторов, действующих на технологическую систему. Систематические погрешности могут возникнуть вследствие изнашивания режущего инструмента или возникновения тепловых деформаций технологической системы до достижения состояния теплового равновесия. Постоянные погрешности проявляются в одинаковой мере при изготовлении каждой детали или изделия. Примером может быть любая геометрическая погрешность металлорежущего оборудования.
Вероятностный подход к явлениям позволяет делать прогнозы появления бракованной продукции в том случае, когда обработку еще не проводили. Предположим, что при изготовлении 1000 деталей 1,5% их оказались бракованными. Если не изменить условия обработки, то во второй тысяче деталей будет примерно этот же процент брака. Этот процент каждый раз будет колебаться вокруг цифры 1,5. Разность максимального и минимального размеров, полученных для партии деталей, называют полем рассеивания размеров. Поле рассеивания размеров характеризует точность обработки: чем меньше поле рассеивания, тем точнее принятый метод и условия обработки.
Процент рассеяния параметров качества, в частности размеров, наилучшим образом характеризуется полигоном распределения. Его легко можно построить для любого массового явления. Все детали (т.е. совокупность измерений) по результатам измерений разбивают на группы. При этом необходимо выполнить условие, чтобы точность измерений не была ниже 0,01 допуска на исследуемый параметр. В каждую группу входят значения, которые находятся в определенных, выбранных интервалах «m» (обычно не менее 10-12 интервалов).
Предположим, что по условиям измерений получены данные.
Таблица 4.1. Результаты измерения деталей
| Интервал размеров | m | Интервал размеров | m | Интервал размеров | m |
| 31,74-31,75 | 31,78-31,79 | 31,82-31,83 | |||
| 31,75-31,76 | 31,79-31,80 | 31,83-31,84 | |||
| 31,76-31,77 | 31,80-31,81 | 31,84-31,85 | |||
| 31,77-31,78 | 31,81-31,82 | 31,85-31,86 |
Эти данные откладывают на оси абсцисс. Число измерений «m», попавших в данный интервал, откладывают по оси ординат. После соединения полученных точек получают ломаную линию, которая и является полигоном распределения.
В технологии машиностроения чаще всего встречается так называемое нормальное распределение. Такое распределение подчиняется нормальному закону, или закону Гаусса, рис.4.1.

Рис.4.1. Кривая нормального распределения с полем допуска  < 6σ
< 6σ
Кривая нормального распределения симметрична, имеет перегиб в точках 1 и 2, ось абсцисс является для нее асимптотой. Такая кривая характеризует ТП, у которых все случайные величины, определяющие конечный результат, слабо влияют друг на друга, а действие каждой случайной величины относительно мало по сравнению с их суммарным действием. Закон удовлетворительно описывает рассеяние размеров деталей на предварительно настроенных станках, массу заготовок и деталей машин, твердость материала, высоту микронеровностей поверхностей. Во многих случаях закон нормального распределения в идеальном виде не наблюдается. На практике приходится наблюдать отклонения от него. Тем не менее, закон нормального распределения оказывается очень удобным для описания рассеяния параметров, а возникающие на практике отклонения можно регламентировать.
Для того чтобы осмысленно использовать на практике анализ точности с помощью математической статистики, необходимо знать, как математически описать кривую нормального распределения. С учетом приведенных на рис.4.1 данных уравнение кривой имеет вид:
 , (4.1)
, (4.1)
где σ – среднее квадратичное отклонение; е – основание натурального логарифма; α – значение абсциссы, при котором ордината достигает максимума.
Величина α является средним арифметическим и одновременно центром распределения или центром группирования. При x = α
y max = 

 (4.2)
(4.2)
Точки 1 и 2 перегиба кривой находятся на расстоянии +σ и -σ от оси симметрии. Их ординаты равны:
упер =  =
= 
 (4.3)
(4.3)
Приближенное построение теоретической кривой Гаусса возможно по пяти точкам, координаты которых даны в табл. 4.2
Таблица 4.2. Координаты точек для приближенного построения кривой Гаусса
| Номер точки | хi | yi |
| x1 = -3σ | у1 = 0 | |
| x2 = -σ | у2 =  = 0,6уmax = 0,6уmax
| |
| х3 = 0 | у3 = уmax = 
| |
| x4 = σ | у4 =  = 0,6уmax = 0,6уmax
| |
| x5 = 3σ | у5 = 0 |
Из уравнения кривой распределения Гаусса следует, что форма кривой и точность обработки определяется величиной среднего квадратичного отклонения σ, чем оно больше, тем ниже точность. При уменьшении величины σ кривая менее растянута, что соответствует меньшему рассеиванию размеров. С каждым более точным этапом обработки значение σ должно уменьшаться. Если этого не происходит, данный ТП применять не следует. Также должны изменяться и значения х1, x 2, х 3.
Значение σ определяют по результатам измерений:
σ =  , (4.4)
, (4.4)
где n – число произведенных измерений; xi - значение текущего измерения;
 - среднее арифметическое значение произведенных измерений,
- среднее арифметическое значение произведенных измерений,
 . (4.5)
. (4.5)
Значения σ и 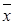 вычисляют, как правило, с помощью ручных калькуляторов. Число измерений рекомендуется брать равным 50 и более. При n=50 погрешность определения σ составляет +10%, при n = 25 она возрастает до +15%.
вычисляют, как правило, с помощью ручных калькуляторов. Число измерений рекомендуется брать равным 50 и более. При n=50 погрешность определения σ составляет +10%, при n = 25 она возрастает до +15%.
При помощи кривой распределения можно определить вероятное число годных деталей и вероятное число бракованных деталей с размерами, выходящими за поле допуска.
Если отложить по оси Х (по обе стороны от нуля) величину ±3σ, то оказывается , что в данном интервале содержится 99,73% (почти 100%) всех величин (отклонений), относящихся к кривой нормального распределения (Гаусса)

Рис.4.2. Пример построения кривой нормального распределения (Гаусса): 1 – гистограмма распределения; 2 – полигон распределения; 3 – теоретическая кривая нормального распределения
Участками кривой Гаусса х > 3σ и х < -3σ можно пренебречь. На основании этого, поле допуска на размер должно быть равно или больше 6σ, т.е. 
 6σ. При расширении поля допуска сверх 6σ вероятность появления брака снижается незначительно.
6σ. При расширении поля допуска сверх 6σ вероятность появления брака снижается незначительно.
1.2. Определение вероятности возникновения брака при обработке
Брак возникает, если допуск на обработку меньше поля рассеивания размеров. Предположим, что поле δ установлено двумя размерами х1 и х2 границ этого допуска от среднего размера (рис.4.1). Вероятное количество годных деталей определяется в этом случае отношением
 , (4.6)
, (4.6)
где F1 и F2 – площади между участками кривых Гаусса и осью абсцисс при размерах х1 и х2; F – площадь между всей кривой Гаусса и осью абсцисс.
При значительном расширении поля допуска (х1 = х2 = 3σ) отношение площадей приближается к единице, так как F1 + F2 = F. В этом случае считают, что вероятность данного достоверного события равна единице.
Определим площади заштрихованных участков F1 и F2 при симметричном распределении кривой распределения относительно оси ординат:
 ,
,  (4.7)
(4.7)
Для удобства расчетов эти интегралы представляют в виде функции Ф(z), введя для этого новую переменную:
 . (4.8)
. (4.8)
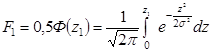 , (4.9)
, (4.9)
 . (4.10)
. (4.10)
Величины F1 и F2 меньше единицы. Они выражают долю от всей площади между кривой Гаусса и осью абсцисс. Площадь между всей кривой Гаусса и осью абсцисс при этом принимают за единицу.
Дата добавления: 2015-04-16; просмотров: 317; Мы поможем в написании вашей работы!; Нарушение авторских прав |