
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Порядок выполнения работы. 3.1. Изучить закон нормального распределения размеров деталей при механической обработке, и уметь описывать кривую нормального распределения.
3.1. Изучить закон нормального распределения размеров деталей при механической обработке, и уметь описывать кривую нормального распределения.
3.2. Научиться с помощью метода математической статистики оценивать точность обработки партии деталей по его представителям.
3.3. Составить отчет о работе.
Пример 1. Определить точность обработки партии корпусных деталей изготовленных в количестве 200шт. Построить полигон распределения размеров изготовленных деталей (измерено 52 детали от партии). Все измеренные размеры разбиты на 12 интервалов с шагом 0,01мм. В каждый интервал попало «m» деталей. Полученные данные по условиям измерений взять из табл. 4.5.
Таблица 4.5. Результаты измерения деталей
| Параметр | Номер варианта | |||||
| Минимальный размер измеренной детали, мм | 25,82 | 37,14 | 40,23 | 52,35 | 68,51 | 74,24 |
| Максимальный размер измеренной детали, мм | 25,93 | 37,25 | 40,34 | 52,46 | 68,62 | 74,35 |
| Число деталей в интервале «m» |
Продолжение таблицы 4.5
| m1 | ||||||
| m2 | ||||||
| m3 | ||||||
| m4 | ||||||
| m5 | ||||||
| m6 | ||||||
| m7 | ||||||
| m8 | ||||||
| m9 | ||||||
| m10 | ||||||
| m11 | ||||||
| m12 |
Пример 2.Определить вероятность получения исправимого и неисправимого брака при растачивании отверстия диаметром 130+0,1мм в партии корпусных деталей в количестве 200 шт., если среднее квадратичное отклонение метода обработки σ = 0,02 мм, а допуск на обработку δ = 0,08 мм. Границы поля допуска, показанные на рис.1, расположены на расстоянии х1 = 0,02 мм и x2 = 0,06 мм от центра группирования. На сколько уменьшится вероятность получения брака по условиям задачи, если центр группирования кривой распределения совместить с серединой поля допуска путем настройки технологической системы?
Решение. Найдем значения z1 и z2 используя формулу (4.8)
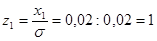 ,
,  .
.
По табл. 4.3 и формулам (4.9) и (4.10):
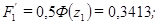
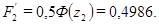 .
.
Вероятность получения брака
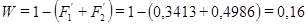 .
.
В случае, если z1 = z2 = z = 0,04 : 0,02 = 2. По табл. 4.3 находим F'1 = F'2 – 0,5Ф(z) = 0,4772.
Вероятность получения брака
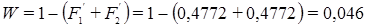 .
.
Во втором случае вероятность получения брака уменьшилась на 11,4 %.
Метод построения кривых распределения размеров сравнительно прост, надежен и поэтому широко применяется для оценки точности размеров деталей при разных методах их обработки. К недостаткам метода следует отнести то, что он в основном дает только суммарную оценку точности обработки и не вскрывает механизм действия разных факторов. Кроме того, метод кривых распределения размеров не учитывает их изменение в процессе обработки при переходе от одной детали к другой, так как вся совокупность деталей рассматривается безотносительно порядка их обработки.
Дата добавления: 2015-04-16; просмотров: 225; Мы поможем в написании вашей работы!; Нарушение авторских прав |