КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Мощность в комплексной форме.

 Возьмем
Возьмем 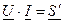 , тогда
, тогда 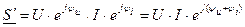 , так как Ψu – Ψi = φ, то:
, так как Ψu – Ψi = φ, то:
|
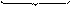
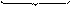

P Q
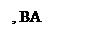

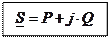


- модуль комплекса полной мощности
| |
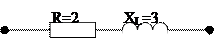 | ||||||||||
| ||||||||||
 | ||||||||||
| ||||||||||
 | ||||||||||
| ||||||||||
| ||||||||||
1.  , A
, A 

2. 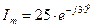 ð
ð 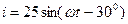
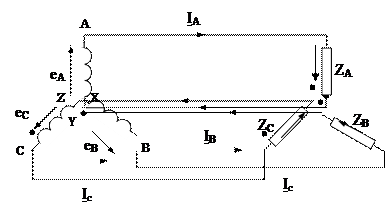
Трёхфазные цепи. Основные понятия.
В электротехнике термин «ФАЗА» применяется в двух различных смыслах:
-Это параметр периодического процесса (аргумент синусоидально меняющейся функции;
-Наименование составной части многофазной системы (однофазная цепь, входящая в состав многофазной).
Объединение в одну цепь нескольких подобных по структуре целей синусоидального тока одной частоты с независимыми источниками энергии широко применяется в технике. Объединяемые цепи принято называть фазами, а всю объединяемую систему – многофазной системой.
 Наибольшее распространение на практике получила трехфазная система. Это объясняется рядом ее преимуществ:
Наибольшее распространение на практике получила трехфазная система. Это объясняется рядом ее преимуществ:
1. Экономичность производства и передачи (меньшее сечение проводов – до 25%)
2. Возможность сравнительно простого получения вращающегося магнитного поля (которое лежит в основе работы АД – самого распространенного двигателя переменного тока) – с помощью неподвижных обмоток трехфазный ток создает вращающееся магнитное поле.
- Получения в одной установке двух эксплуатационных
напряжений – фазного и линейного (при 4-х проводной системе)
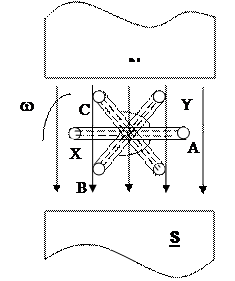
3фазный переменный
ток может быть получен
при помощи 3 витков
|
 вращаемых в однородном
вращаемых в однородном
 магнитном поле с
магнитном поле с
|

 постоянной скоростью (w)
постоянной скоростью (w)
если ветки сдвинуты друг
относительно друга под 120
|
|
| |

 |
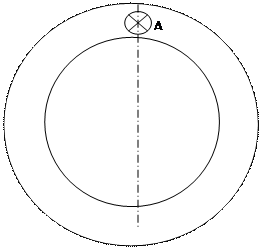
На практике для получения трехфазного тока в пазах статора генератора переменного тока помещают трехфазные обмотки, сдвинутые в пространстве друг относительно друга на 120о. Они называются фазными обмотками.
Начала и концы обмоток обозначают соответственно A,B,C и X,Y,Z, а сами обмотки называют фазами
 | |||
 |
|
|

|

|


|
 |
Модель трехфазного генератора
2. По закону электромагнитной индукции в обмотках наводятся ЭДС
eA = Em*sinwt
eB = Em*sin(wt-120o)
eC = Em*sin(wt-240o)
|

| |

| |


|



 |
4. Комплексные числа
EA = E*ejo= EA
EB = E*e-j120o= E*[cos(-120o) + j*sin(-120o)] = E(-1/2 – j*Ö3/2)
EC = E*ej120o= E(-1/2 + j*Ö3/2)
На комплексной плоскости:

 |

| |||
 | |||
Т.о. под трехфазной системой понимают совокупность переменных э.д.с. (токов, напряжений) одной частоты, равных по амплитуде,и сдвинутых по фазе относительно друг друга на 120о.
Трехфазная система может изображаться:
1) графиками;
2) тригонометрическими функциями;
3) векторами;
4) функциями комплексной системы.
Для симметричной трехфазной системы: ЕА + ЕВ + ЕС = 0
Система, в которой фаза В отстает по фазе от фазы А, а фаза С от э.д.с. фазы В называется прямой последовательностью фаз, если изменить последовательность, то последовательность будет называться обратной.
Поскольку на практике применяется прямая последовательность фаз, мы будем рассматривать только такую.
На схемах обмотку (или фазу) источника питания изображают следующим образом:
 |
Несвязная шестипроводная система – на практике не применяется в виду большого количества проводов. Каждая фаза соединена 2 проводами, между собой фазы электрически не соединены.
Более совершенными и экономичными являются связанные цепи, в которых фазы обмотки соединены электрически.

 Соединение фаз может быть различным: треугольник « » ,звезд « », зигзаг «U»
Соединение фаз может быть различным: треугольник « » ,звезд « », зигзаг «U»
 Наибольшее распространение на практике получили соединения: U,
Наибольшее распространение на практике получили соединения: U,
предложенные М.О.Доливо-Добровольским в начале 90-х годов прошлого века.
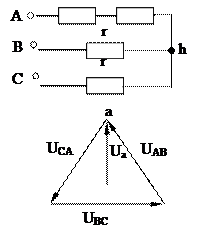
Соединение «звездой»
Если все концы фаз (X, Y, Z) соединить вместе, а оставшиеся 3 провода присоединить к линейным проводам, то получим соединение “Y”.
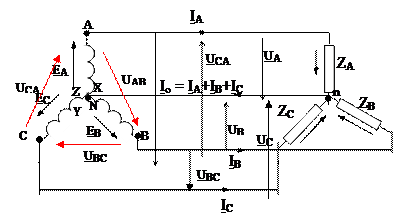 |
Нулевая точка Г – (N)
Нулевая точка потребителя потребителя – (n)
Провод, соединяющий нулевые точки, называется нейтральным. Остальные три провода – линейные.
Ток в нейтральном проводе Io = IA + IB + IC = 0
при симметричной трехфазной системе, т.е. zA = zB = zC !
Напряжение между нейтральным проводом и любым из линейных проводов – называется фазным напряжением : Uф (UA, UB, UC).
Напряжение между любыми двумя линейными проводами называется линейным : Uл (UAB, UBC, UCA).
Э.д.с. фазных обмоток генератора Eф (EA; EB; EC)
EA = Em
EB = Em*e-j120o= Em[(-1/2) – jÖ3/2]
Ec = Em*ej120o= Em[(-1/2) + jÖ3/2]
EA + EB +EC = 0
Пренебрегая сопротивлением обмоток Г и провода можно записать, что
EA = UA; EB = UB; EC =UC
UAB = UA – UB
UBC = UB – UC
UCA = UC – UA
При симметричной нагрузке ток в нейтральном проводе = 0, поэтому этот провод можно убрать (например, включение трехфазных двигателей, трансформаторов и т.д.).
При несимметричной нагрузке по нейтральному проводу потечет определенный ток (равный геометрической сумме фазных токов).
Т.к. по фазным проводам протекает такой же ток, что и по линейным, то
|
Определим соотношение между Uф и Uл
 |
При симметричной нагрузке: UA = UB = UC = Uф
Построим треугольник линейных напряжений и звезду фазных напряжений.
|
 из треугольника OBK: cos30o = (UBC/2)/UB UBC = 2UB*cos30o = Ö3UB или
из треугольника OBK: cos30o = (UBC/2)/UB UBC = 2UB*cos30o = Ö3UB или
Если нагрузка несимметричная, то это условие не выполняется.
 UA = EA – UNn Где UnN -- напряжение смещения нейтрали, которое может
UA = EA – UNn Где UnN -- напряжение смещения нейтрали, которое может
UB = EB – UNn быть определено с использованием метода 2 узлов:
 UC = EC – UNn UNn=YA*EA + YB*EB + YC*EC =
UC = EC – UNn UNn=YA*EA + YB*EB + YC*EC =
YA + YB + YC + Yn
= (Uл*(YA + a2YB + aYC)) / (Ö3*(YA +YB + YC +Yn))
Векторные диаграммы трехфазной системы, соединенной «звездой»
1. Равномерная (симметричная)
 |


 IA = UA/ZA ; IB = UB/ZB ; IC = UC/ZC ;
IA = UA/ZA ; IB = UB/ZB ; IC = UC/ZC ;
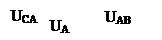 |
|
|
|


 IA = IB = IC
IA = IB = IC
|
 cosjA = RA/ZA ; cosjB = RB/ZB ; cosjC = RC/ZC ;
cosjA = RA/ZA ; cosjB = RB/ZB ; cosjC = RC/ZC ;
|
cosjA = cosjB = cosjC
2. Неравномерная (активная)
|
|
 |
|
|
|

 UNn- узловое напряжение
UNn- узловое напряжение
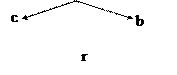 |
 б)
б)
 |
UNn- узловое напряжение

Частные случаи (аварийные) в трехпроводной системе «звезда»
а) обрыв фазы «А»
(получим однофазную систему)
 | |||
 | |||
б) короткое замыкание фазы «А»
 | |||
 | |||
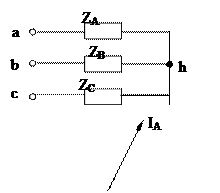
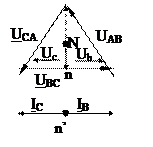
Трехфазная система, соединенная «треугольником».
 |
Если конец одной фазы соединить с началом 2-й, конец 2-й с началом 3-й и конец 3-й с началом 1-й, то получим соединение «треугольником».

Линейные напряжения равны соответствующим фазным
|
По 1-у закону Кирхгофа:
IA = Iaв – Ica
IB = Iвc – Iaв
IC = Ica - Iвc
Комплексные значения фазных токов:
Iaв = Uaв/Zaв ; Iвc = Uвc/Zвc ; Ica =Uca/Zca
Преимуществом соединения трехфазной системы по схеме «треугольник» является взаимная независимость фазных токов (при обрыве одного из линейных проводов, например В, напряжение фазы «ca» остается нормальным, а в 2-х других имеет место последовательное включение, фазы «ав» и «вс» находятся под напряжением в половину меньшим).
Изобразим треугольник линейных токов и звезду фазных токов для симметричной нагрузки:
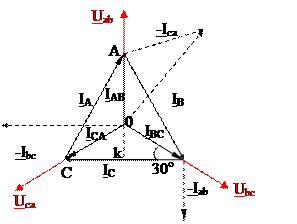 |
|


из треугольника OBK: (Ic/2)/Iвc = cos30o = Ö3/2
|
2) Для симметричной трехфазной системы
Векторные диаграммы трехфазной системы, соединенной «треугольником»
Несимметричная нагрузка
RAB > RBC > RCA
|
|

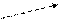 IA = Iab - Ica
IA = Iab - Ica


 IB = Ibc – Iab
IB = Ibc – Iab
|
|
|
 |
|
 Узловая точка остается на месте, а векторная
Узловая точка остается на месте, а векторная
|
|
 диаграмма может деформироваться.
диаграмма может деформироваться.
IA+IB+IC = Iab-Ica+Ibc-Iab+Ica-Ibc = 0
Таким образом, сумма линейных токов (при симметричной и несимметричной нагрузке) = 0.
Частные (аварийные) случаи
а) обрыв фазы «аb»
 Iab = 0IA = -Ica
Iab = 0IA = -Ica
IB = Ibc
IC = Ica – Ibc
|
|
|
|




 |
б) обрыв двух фаз: «ab» и «bc»
 Iab = 0 ; Ibc = 0 IA = -Ica
Iab = 0 ; Ibc = 0 IA = -Ica
IB = 0 IA = -IC
|
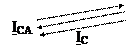
в) обрыв линейного провода : «В»
 IB = 0 Ibc = Iab = ½*Iac
IB = 0 Ibc = Iab = ½*Iac
IA = Iab – Ica IA = -IC
IC = Ica – Iab
 |



 |
Мощность трехфазной системы
Для однофазной системы P = Uф*Iф*cosj , Вт
Для симметричной нагрузки трехфазной системы: P3ф = 3Pф :
P3ф = 3Iф*Uф*cosj
“Y”: Iл = Iф ; Uл = Ö3Uф
P = 3I*(Uл/Ö3)*cosj = Ö3I*U*cosj ,Вт
 P = Ö3Uл*Iл*cosj , Вт
P = Ö3Uл*Iл*cosj , Вт
 S = 3Uл*Iл , ВА
S = 3Uл*Iл , ВА
 “ “ Iл = Ö3Iф ; Uл = Uф
“ “ Iл = Ö3Iф ; Uл = Uф
P = 3U*(Iл/Ö3)*cosj = Ö3I*U*cosj ,Вт
P = Ö3Iл*Uл*cosj
Таким образом,
P = 3Iф*Uф*cosj P = Ö3Iл*Uл*cosj
Q = 3Iф*Uф*sinj Q = Ö3Iл*Uл*sinj
S = 3Iф*Uф S = Ö3Iл*Uл
Эти формулы справедливы только для симметричной нагрузки
Активная мощность в трехфазных цепях при симметричной нагрузке, соединенных по схеме Y, а также при возможности включения последовательной обмотки ваттметра в фазную цепь электроприемников, соединенных «треугольником» может быть измерена одним прибором, указывающем фазную величину мощности:
Pф = Uф*Iф*cosj
 “Y” “ “
“Y” “ “
 | |||
 | |||

P3ф = 3Pф
Если нет доступной нейтральной точки, применяют искусственную нулевую точку
|
|
|
|





 “Y”
“Y”
 |
rA + rВт = rB + rC
rВт – активное сопротивление параллельной обмотки ваттметра

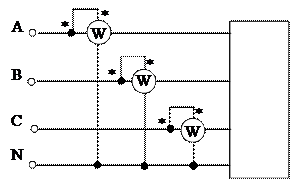
При несимметричном режиме измерение активной мощности можно выполнить двумя однофазными ваттметрами или одним трехфазным двухэлементным прибором:
 |
общая мощность – сумма показаний обоих ваттметров
 P3ф = PAB + PCB
P3ф = PAB + PCB
p = uA*iA + uB*iB + uc*ic
iA + iB + iC = 0
iB = (iA + iC)
P3ф = uA*iA – uB*(iA + iC) + uC*iC = uAB*iA + uCBic = PAB + PCB
|
Примеры трехфазной системы :
1) симметричный электроприемник – трехфазный двигатель с соединением трехфазных обмоток по схеме «звезда»
Дата добавления: 2015-04-16; просмотров: 298; Мы поможем в написании вашей работы!; Нарушение авторских прав |
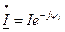 , тогда
, тогда