Нейтральный провод отсутствует

	статор				статор
	ротор
				ротор

Асинхронный двигатель

коротко замкнутый Асинхронный двигатель

с фазным ротором

осветительная нагрузка по схеме «звезда»

3) осветительная нагрузка по схеме «треугольник»

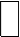
ОСОБЕННОСТИ ЭЛЕКТРОМАГНИТНЫХ ПРОЦЕССОВ В ОБМОТКАХ ЭЛЕКТРОТЕХНИЧЕСКИХ УСТРОЙСТВ.

При подключении катушки к источнику синусоидального напряжения u(t)=U_msinωt переменный ток i (его намагничивающая сила) обмотки возбуждает в магнитопроводе переменный магнитный поток Ф: Ф = (Ф_осн + Ф_р).

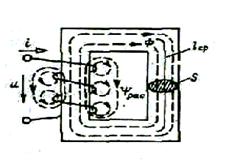
i (t) = ?

Ф (t) = ?

e (t) = ?

U → I∙W → Ф = (Ф_осн + Ф_р) → Е

намагничивающая

сила

Ф = - ЗАКОН ОМА ДЛЯ МАГНИТНОЙ ЦЕПИ, где

W – число витков,

l – длина средней магнитной силовой линии,

S – площадь магнитопровода,

μ – магнитная проницаемость материала сердечника.

При подключении обмотки к источнику синусоидального напряжения магнитный поток также синусоидальный при определённых допущениях, а величина э.д.с. определяется изменением магнитного потока. Тогда закон изменения э.д.с. принимает вид:

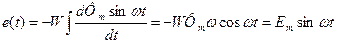
При синусоидально изменяющемся магнитном потоке основной параметр э.д.с. изменяется также по синусоидальному закону, но характеризуется сдвигом фаз по отношению к магнитному потоку π/2.

E_m = W 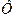_m = 2π f W 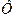_m

E = E_m/2 = f W 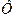_m = 4.44 f W 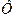_m

E = 4.44 f W 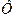_m – ОСНОВНАЯ ФОРМУЛА Э.Д.С. ОБМОТКИ ЛЮБОГО ЭТУ

Это уравнение часто используют для расчетов э.д.с. индуктируемых в обмотках трансформаторов, поэтому его часто называют уравнением трансформаторной э.д.с.

энергетический баланс обмотки; составляющие потерь.

Р_к = U∙I∙cosφ = Р_м+Р_ст

Р_к = Р_м+Р_ст – энергетический баланс обмотки,

где Р_м- потери, связанные с нагревом обмотки («в меди»)

Р_ст- потери в стали = в сердечнике («магнитные потери»)

Р_меди = Р_эл = I²∙R

Р_ст = Р_магн = Р_в.т. + Р_г

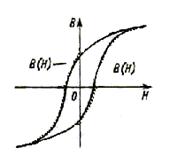Зависимость В от Н характеризует свойства материала сердечника, которое

существенно влияет на характер тока, протекающего по обмотке, который может быть получен при рассмотрении зависимости В(Н).

Рассмотрим режим намагничивания магнитопровода идеализированной катушки, подключенной к источнику синусоидальной э.д.с.

При синусоидально изменяющемся напряжении закон изменения тока несинусоидальный. Полученные построения показывают, что при синусоидальном магнитном потоке кривая намагничивающего тока отлична от синусоидальной вследствие явлений, характеризуемых зависимостью B=f(H) (явление насыщения гистерезиса).

уравнение электрического состояния обмотки.

схемы замещения

Схема замещения – это электрическая модель, на которой смоделированы все конструктивные элементы и соблюдены все основные соотношения.

Последовательная схема замещения:

R_k – моделирует сопротивление провода обмотки

X_k - моделирует сопротивление рассеяния обмотки.

Участок аb с параллельным соединением двух элементов, разных по характеру, позволяет выделить активные и реактивные составляющие тока, протекающего по обмотке. Тогда активная составляющая тока I_a определит потери в магнитопроводе, а I_р – намагничивающий ток. Учитывая величину активного сопротивления обмотки R_k , наличие магнитного потока рассеяния (Ф_р), замыкающегося в воздухе, можно найти связь между приложенным напряжением U, э.д.с., наведённой основным магнитным потоком, падением напряжения на R_k и э.д.с., обусловленной магнитным потоком рассеяния, в виде уравнения, полученного на основании 2 закона Кирхгофа:

U = -E + I∙R - E_p

U = -E + I∙R + j x – уравнение электрического состояния цепи.

Схема замещения как электрическая модель позволяет легко проиллюстрировать уравнение электрического состояния обмотки на основании законов электрических цепей.

, См

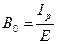, См Если параметры R_k, X_k не учитывать, то говорят об идеализированной катушке. Характеризующие её параметры: G₀, B₀, U_ab.

Векторная диаграмма – иллюстрация уравнения электрического состояния обмотки и других параметров, характеризующих работу устройства:

Вектор тока опережает вектор магнитного потока на угол δ , называемый углом потерь идеализированной катушки.