Эквивалентные преобразования пассивных электрических цепей.

Эквивалентное преобразование части пассивной электрической цепи состоит в такой ее замене другой пассивной цепью, при которой остаются неизменными токи и напряжения остальной цепи, не подвергшейся преобразованию. К простейшим преобразованиям относятся замена последовательно и параллельно соединенных потребителей эквивалентным потребителем.

При последовательном соединении роль эквивалентного сопротивления играет сумма сопротивлений всех потребителей (рис. 1.11.).

(II З. К.) =>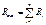

При параллельном соединении роль эквивалентной проводимости (или проводимости эквивалентного потребителя) играет сумма проводимостей всех потребителей (рис. 1.12.).

Это следует из I закона Кирхгофа:

9-10) Эквивалентное преобразование «Звезда – треугольник»

В узлах a, b, c и треугольник , и звезда на рис. 1.14. соединяются с остальной частью схемы. Преобразование треугольника в звезду должно быть таковым, чтобы при одинаковых значениях потенциалов одноименных точек треугольника и звезды притекающие к этим точкам токи были одинаковы, тогда вся внешняя схема «не заметит» произведенной замены.

Выразим U_abтреугольника через параметры потребителей и притекающие к этим узлам токи. Запишем уравнения Кирхгофа для контура и узлов a и b.

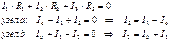
Заменим в первом уравнении токи I₃ и I₂на соответствующие выражения:

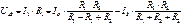
Теперь получим выражение для этого же напряжения при соединении потребителей звездой:

=>

Аналогично

Таким образом, сопротивление луча звезды равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений трех сторон треугольника.

Формулы обратного преобразования можно вывести независимо, либо как следствие соотношений через проводимости:

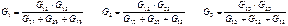
или через сопротивления: