
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Контурных Токов
За искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по II закону Кирхгофа, т.е. 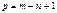 . Основан на II законе Кирхгофа
. Основан на II законе Кирхгофа
По найденным контурным токам при помощи I закона Кирхгофа определяются токи ветвей.
Таким образом, методика расчета цепи постоянного тока методом контурных токов следующая:
1. Обозначить все токи ветвей и их положительное направление.
2. Произвольно выбрать совокупность p независимых контуров, нанести на схему положительное направление контурных токов, протекающих в выбранных контурах.
3. Определить собственные, общие сопротивления и контурные ЭДС и подставить их в систему уравнений вида.
Общее сопротивление контура (Rij = Rji) представляет собой алгебраическую сумму сопротивлений потребителей ветви (нескольких ветвей), одновременно принадлежащих i-ому и j-ому контурам. В эту сумму сопротивление входит со знаком «+», если контурные токи протекают через данное сопротивление в одном направлении (согласно), и знак «–», если они протекают встречно.
Собственное сопротивление контура (Rii) представляет собой арифметическую сумму сопротивлений всех потребителей, находящихся в i-ом контуре.
Контурные ЭДС представляют собой алгебраическую сумму ЭДС источников, входящих в контур. Со знаком «+» в эту сумму входят ЭДС источников, действующих согласно с обходом контура, со знаком «–» входят ЭДС источников, действующих встречно.
4. Разрешить полученную систему уравнений относительно контурных токов, используя метод Крамера.

5. Определить токи ветвей через контурные токи по I закону Кирхгофа.
6. Проверить правильность расчетов при помощи баланса мощности.
Если в цепи содержится q источников тока, количество совместно рассматриваемых уравнений сокращается на q и становится равным р – q, поскольку токи в таких ветвях известны Необходимо, чтобы каждый источник тока входил только в один контур.
Дата добавления: 2015-04-16; просмотров: 237; Мы поможем в написании вашей работы!; Нарушение авторских прав |