Пример расчета модели непосредственно на графике

(секторным методом)

Рассмотрим небольшую сетевую модель, представленную в

виде сетевого графика на рис. 1. На графике продолжительность работ в днях указана числами над соответствующими работами. Момент наступления исходного события условно принят равным нулю (То = 0).

При расчете вручную события следует изобразить так, как показано на рис. 2. Вначале определяются ранние сроки работ

, и расчет ведется от исходного события к завершающему, т.е. слева направо, с заполнением левых секторов.

В числителе Rп – полный резерв времени.

В знаменателе Rc – свободный резерв времени.

Рис. 1. Исходная сетевая модель при расчете непосредственно на

графике (продолжительность работ указана над стрелками)

Рис. 2. Изображение событий при расчете сетевой модели

непосредственно на графике

В левый сектор исходного события записывается нуль, так как по условию Т0 = 0, в нижний сектор – тоже нуль, у исходного события нет предшествующих работ (рис. 3.)

Ранний срок последующих работ равен наибольшему значению ранних окончаний работ, входящих в данное событие.

Например, для события 7 (работа 7–9):

= max = max = 15.

Рис. 3. Порядок расчета сетевой модели непосредственно

на графике; (секторным методом) критический путь выделен

В левый сектор события 7 записываем 15 – ранний срок наступления событий 7, в нижний сектор записываем 3 – номер события, через которое к данному проходит путь максимальной продолжительности. Подобным образом определяются ранние

сроки наступления всех событий и работ.

В левый сектор завершающего события 9 заносим максимальную величину из ранних сроков окончания работ, входящих в данное событие, - это и будет минимальное время, в течение которого может быть выполнен весь комплекс работ:

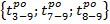= max = max = 25+11 = 36 дней

В левый сектор завершающего события проставляем 36.

В нижний сектор завершающего события 9 заносим номерсобытия 8, через которое идет путь максимальной продолжительности. Таким образом, Ткр = 36 дней.

Далее определяются работы, принадлежащие критическомупути. Критический путь проходит через завершающие событие 9, в нижнем секторе которого записано 8. Следовательно, событие 8 принадлежит критическому пути. В нижнем секторе

события 8 записано 7, т.е. критический путь пройден через событие 7, и т.д. до исходного события. Критический путь в рассматриваемом примере проходит через события 1,2,3,7,8,9, и он выделяется на графике.

Затем определяются поздние сроки работ. Расчет ведется от завершающего события к исходному, т.е. справа налево. Поздний срок наступления завершающего события задан и равен:

= +4 = 36 +4 = 40 дней

Поэтому в первый сектор завершающего события 9 записываем 40.

Поздний срок окончания предшествующих работ равен минимальному значению поздних начал работ, выходящих из данного события.

Например, для события 7:

Из этого события выходят две работы 7-8 и 8-9, которые имеют поздние сроки окончания

= 29 и = 40.

Тогда их поздние начала будут

= 29-10=19 и =40-7=37 дней.

В правый сектор события 7 записываем минимальное значение 19 дней.

Таким образом определяют значения поздних окончаний других работ и заполняют правые сектора событий.

Для события 2:

Из него выходят четыре работы.

= min =min = 14-8=6 дней.

В правый сектор события 2 записываем 6 и т.д.

После определения ранних и поздних сроков наступления

событий определяются резервы времени для всех работ.

Например, для работы 4–6:

= = 23-2-4=17 дней.

Резервы времени работ записываются непосредственно на графике под работами в квадрате: в числителе – полный, в знаменателе – свободный резервы.