Резонансные явления в цепи переменного тока.

Резонанс – такой режим работы элементов цепи, при котором она ведет себя, по отношению к источнику энергии, как чисто активное сопротивление, т.е. напряжение и ток совпадают по фазе.

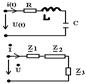Резонанс напряжения:

z₁=R;

z₂=jwL=jX_L;

z₃=-j/wc=-jX_C;

z=z₁+z₂+z₃=R+jX_L-jX_C=R+j(X_L-X_C);

X_L=X_C – условие резонанса напряжения.

wL=1/wC;

w₀=1/Ö(LC) – резонансная частота.

Сопротивление любого реактивного элемента по резонансной частоте называется характеристическим сопротивлением последовательного колебания контура.

r=w₀L=1/w₀C=Ö(L/C).

Добротностью контура называется отношение характеристического сопротивления контура к его активному сопротивлению:

q=r/R.

Замечание:

Резонанс напряжения характеризуется следующим:

1. Ток в режиме резонанса maх: I·_рез=U·/Z =U·/R;

2. Напряжения на реактивных элементах возрастают в q-раз по отношению к напряжению источника питания:

U_L=X_LI_рез;

U_C=X_CI_рез;

U_L=U_C;

U·_R+U·_L+U·_C=I·_резR+I·_резjX_L+I·_рез(-jX_C)=I·_резR+I·_резj(X_L-X_C)=I·_резR; U_L/U=U_C/U=rI_рез/RI_рез=r/R=q.

3. Реактив. мощность Q_L u Q_C равны между собой, а активная мощность максимальная.

P=I²_резR;

Q=Q_L-Q_C=I²_резX_L-I²_резX_C=I²_рез(X_L-X_C)=0;

Реактив мощность, потребляемая контуром, равна 0.

Векторная диаграмма – совокупность векторов комплексных значений синусоидальных величин.

U_L=U_C;

Q_C=Q_L;

Cos(φ)=1 – коэффициент мощности.

15. Резонанс токов. Векторная диаграмма.

Резонанс токов:

z₁=R₁;

z₂=jwL=jX_L;

z₃=R₃;

Величина обратная контурному сопр-ю наз. комп. проводн.

Y·=1/Z=U·Y·=U·(g+jb)=U·g+U·jb=

=I·_A+jI·_P;

Y·₁=1/(z₁+z₂)=1/(R₁+jX_L)=(R₁-jX_L)/(R₁²+X_L²)=(R₁/(R₁²+X_L²))–j(X_L/(R₁²+X_L²));

(R₁/(R₁²+X_L²))=g₁ – активная проводимость ветви1.

(jX_L/(R₁²+X_L²))=b_L – индуктивная проводимость контура.

Y·₂=1/(z₃+z₄)=1/(R₂-jX_С)=(R₂+jX_С)/(R₂²+X_С²)=(R₂/(R₂²+X_С²))+j(X_С/(R₂²+X_С²));

(R₂/(R₂²+X_С²))=g₂ – активная проводимость ветви 2;

(jX_С/(R₂²+X_С²))=b_C – емкостная проводимость контура;

Y·=Y·₁+Y·₂=g₁-jb_L+g₂+jb_C=g₁+ g₂+j(b_C-b_L);

I·=U·Y·=U·(g+j(b_C-b_L));

b_C=b_L – условие резонансов токов;

R₁=R₂=0;

b_L=1/X_L=1/wL;

b_C=1/X_С=1/(1/wС)=wС;

b_L=b_C =>1/wL=wC;

w’₀=Ö(1/LC) – резонансная частота ||-го контура без потерь,

r=Ö(L/C) – характеристическое сопротивление ||-го контура без потерь,

w₀=Ö((r²-R₁²)/(r²-R₂²)) – резонансная частота ||-го контура.

Резонансной частотой колебательного контура опр-ся не только параметрами реактив. эл-ов вх-х в контур, но и параметрами активных эл-в, т.е. R₁ и R₂. Если R₁=R₂=r - резонанс наступает на любых частотах.

Резонанс токов хар-ся след:

1. Полная проводимость контура=активной проводимости, а значит минимальна. Ток в неразветвл. части цепи минимален.

2. Реактивн. состояния токов в ветвях максимальны и противопол. по фазе.

3. Реактивные мощности Q_L и Q_C равны, а их суммарная реактивная мощность контура=0. Q_L=U²b_L; Q_С=U²b_С; Q= Q_L-Q_C= U²(b_L-b_C)=0;