
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
СТАТИСТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ТОЧНОСТИ
Виды погрешностей.Погрешности, возникающие при выполнении заготовок, механической обработке, техническом контроле, сборке и других видах обработки, можно разбить на три вида: систематические постоянные, систематические закономерно изменяющиеся и случайные.
Систематические постоянные погрешности не изменяются при обработке одной или нескольких партий заготовок. Они возникают под влиянием постоянно действующего фактора. Примером подобных погрешностей могут служить: неперпендикулярность оси просверленного отверстия к базовой плоскости заготовки из-за неперпендикулярности оси шпинделя к плоскости стола вертикально-сверлильного станка; ошибки межосевого расстояния растачиваемых отверстий из-за неправильно выдержанного расстояния между осями направляющих втулок расточного кондуктора; погрешность формы обтачиваемой поверхности (конусность) в результате непараллельности оси шпинделя направляющим станины токарного станка. Систематические постоянные погрешности могут быть выявлены пробными измерениями нескольких обработанных деталей. Эти погрешности сводятся к желаемому минимуму соответствующими технологическими мероприятиями.
Систематические закономерно изменяющиеся погрешности могут влиять на точность обработки непрерывно или периодически! Примером непрерывно влияющей погрешности может служить погрешность, вызываемая размерным износом режущего инструмента. Примером периодически действующей погрешности может служить погрешность, возникающая в результате тепловой деформации станка в период его пуска до достижения состояния теплового равновесия.
Знание закона изменения этих погрешностей позволяет принимать меры для их устранения или уменьшения при построении станочных операций.
Случайные погрешности возникают в результате действия большого количества несвязанных между собой факторов. Случайная погрешность может иметь различное значение; определить заранее момент появления и точную величину этой погрешности для каждой конкретной детали в партии не представляется возможным. Случайные погрешности могут быть непрерывными и дискретными. Непрерывная случайная погрешность может иметь любые численные значения в границах определенного интервала. Основная масса случайных погрешностей носит непрерывный характер. Примерами непрерывных случайных погрешностей могут служить погрешности положения заготовки на станке, а также погрешности обработки, вызываемые упругими отжатиями элементов технологической системы под влиянием нестабильных сил резания. Дискретные случайные погрешности в технологии машиностроения встречаются редко. К ним можно, в частности, отнести погрешности регулировки при использовании устройств ступенчатого типа.
Причинная связь между случайной погрешностью и вызывающими ее появление факторами иногда бывает известной (явной), а иногда не вполне выясненной. Так, например, для конкретного случая обработки может быть выявлена зависимость упругих отжатий технологической системы от величины снимаемого припуска. Факторы, вызывающие разброс диаметров отверстий, обработанных одной разверткой, являются пока полностью невыясненными.
Несмотря на то, что определение случайной погрешности для каждой детали в партии практически неосуществимо, можно тем не менее установить пределы изменения этой погрешности. При явно выраженной связи между случайной погрешностью и вызывающими ее появление факторами пределы изменения случайной величины могут быть определены аналитическими расчетами. Например, разность предельных расстояний от измерительной базы до обрабатываемой поверхности, представляющую собой погрешность базирования, можно заранее вычислить, зная допуски на размеры заготовки. При неявной (невыявленной) связи между случайной погрешностью и влияющими на ее появление факторами пределы изменения случайной величины могут быть установлены на базе экспериментальных исследований.
В процессе изучения явлений невыявленные ранее связи становятся явными. В результате этого можно более полно учитывать влияние различных технологических факторов на точность механической обработки при разработке технологических процессов,
Кривые распределения и оценка точности обработки.Сущность статистического метода оценки точности достаточно подробно изложена в специальной литературе и в трудах по технологии машиностроения. Этот метод применим в условиях производства большого количества одинаковых деталей, обрабатываемых как на предварительно настроенных станках, так и методом пробных проходов.
Математическая статистика была той научной базой, на которой начали проводить первые исследования точности технологических процессов. Первым шагом в этом направлении было изучение и анализ кривых распределения. Построение кривых распределения производится следующим образом. Всю совокупность измерений* интересующей нас величины (например, какого-либо размера в партии заготовок, обработанных при определенных условиях) разбивают на ряд групп. В каждую группу входят величины, результаты измерения которых находятся в пределах установленного интервала. Интервалы, число которых обычно берут в пределах 7—11, откладывают по оси абсцисс, а количество замеров, приходящееся на каждый интервал, по оси ординат. После соединения нанесенных на график точек получают ломаную линию, называемую полигоном распределения. На рис. 17, а показан полигон распределения диаметральных размеров колец, подвергнутых предварительному обтачиванию; из него видно, что на средине интервалы размеров приходится большее количество колец. При увеличении количества деталей в партии, сужении интервалов и увеличении их числа ломаная линия приближается к плавной кривой.
Вместо абсолютного количества т деталей в каждом интервале по оси ординат откладывают также отношение этого количества к общему количеству n , деталей в партии; данное отношение называется относительной частотой, или частостью.
В качестве самой приближенной меры точности исследуемого процесса обработки может служить поле рассеяния размеров (см. рис. 17,а). Величину поля рассеяния можно брать по полигону распределения или по таблице измерения исследуемых значений. Чем уже поле рассеяния, тем точнее исследуемый технологический метод.
Вид кривой распределения определяется количеством и характером факторов, влияющих на исследуемую величину. Многочисленные исследования показали, что в технологии машиностроения распределение размеров чаще всего происходит по так называемому нормальному закону или закону Гаусса. Соответствующая кривая распределения (рис, 17, б) имеет симметричную шатрообразную форму.
Нормальный закон распределения имеет место в тех случаях, когда исследуемая случайная величина является результатом действия большого числа различных факторов, причем все факторы по интенсивности своего влияния, действуют одинаково. Этому закону подчиняются многие непрерывные случайные величины: размеры деталей, обработанных на настроенных станках, вес заготовок и деталей машин, твердость и другие характеристики механических свойств материала, 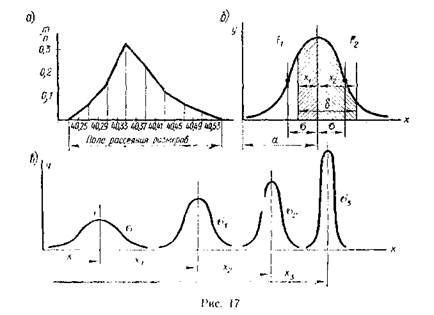
высота микронеровностей па обработанных поверхностях, погрешности измерений и некоторые другие величины. Практически почти всегда во всех перечисленных случаях приходится наблюдать небольшие отклонения от нормального закона. Эти отклонения обычно непостоянны во времени для номинально одних и чех же условий обработки. Кривая Гаусса выражается следующим уравнением:
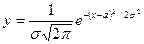
Здесь 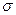 — среднее квадратичное отклонение аргумента; е — основание натуральных логарифмов; а значение абсциссы, при которой ордината у кривой достигает максимума; величина а является центром распределения (группирования) аргумента и в то же время его средней арифметической.
— среднее квадратичное отклонение аргумента; е — основание натуральных логарифмов; а значение абсциссы, при которой ордината у кривой достигает максимума; величина а является центром распределения (группирования) аргумента и в то же время его средней арифметической.
Закон Гаусса двухпараметрический (параметры 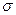 и а). Ордината вершины кривой при х = а
и а). Ордината вершины кривой при х = а
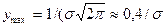
Точки перегиба кривой лежат на расстояниях σ от её оси симметрии (см. рис. 17, б). Их ординаты
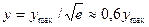
Величина среднего квадратичного отклонения 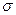 , являющаяся мерой точности характеризует форму кривой распределения. При больших значениях а кривая получается очень пологой и поле рассеяния растет. При малых значениях
, являющаяся мерой точности характеризует форму кривой распределения. При больших значениях а кривая получается очень пологой и поле рассеяния растет. При малых значениях 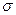 точность исследуемого метода повышается и кривая получается сильно вытянутой вверх с малым полем рассеяния. На рис. 17, в показаны кривые распределения диаметральных размеров цилиндрического отверстия на различных этапах его обработки. Кривая
точность исследуемого метода повышается и кривая получается сильно вытянутой вверх с малым полем рассеяния. На рис. 17, в показаны кривые распределения диаметральных размеров цилиндрического отверстия на различных этапах его обработки. Кривая 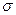 характеризует распределение размеров отверстия в исходной заготовке; кривая
характеризует распределение размеров отверстия в исходной заготовке; кривая 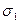 — распределение размеров после предварительной обработки, а кривые
— распределение размеров после предварительной обработки, а кривые 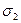 и
и 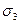 — соответственно после чистовой и окончательной обработок. При правильном построении технологического процесса обработки необходимо выполнять условие
— соответственно после чистовой и окончательной обработок. При правильном построении технологического процесса обработки необходимо выполнять условие 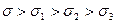 , так как на каждом последующем переходе обработки должна обеспечиваться более высокая точность, чем на предыдущем. Кроме того, величины х3 — х2, х2 — х1 и х1 - х должны быть достаточно большими во избежание брака при обработке. Определение
, так как на каждом последующем переходе обработки должна обеспечиваться более высокая точность, чем на предыдущем. Кроме того, величины х3 — х2, х2 — х1 и х1 - х должны быть достаточно большими во избежание брака при обработке. Определение 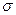 по результатам измерений производят по следующей формуле:
по результатам измерений производят по следующей формуле:
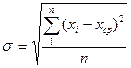 , (11)
, (11)
где п — количество произведенных измерений; xi — значение текущего измерения; xср — среднее арифметическое из произведенных измерений
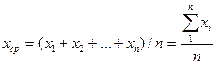 . (12)
. (12)
Количество измерений п рекомендуется брать равным 50. При этом погрешность определения 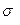 равна ±10%. Если п = 25, погрешность определения
равна ±10%. Если п = 25, погрешность определения 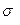 возрастает до ±15%. Для определения среднего арифметического с той же погрешностью количество измерений можно брать в 5. раз меньше.
возрастает до ±15%. Для определения среднего арифметического с той же погрешностью количество измерений можно брать в 5. раз меньше.
Определение величин 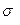 и xср удобно производить, занося данные
и xср удобно производить, занося данные
измерений и вычислений в таблицу. Пример вычислений приводится
в табл. 1.
Таблица 1
Пример вычисления σ
| № п.п. | xi | xi-xср | (xi-xср)2 |
| . . . . . . | 62,74 62,75 62,83 . . . . . . . . . . . . 62,81 | 0,05 0,04 0,04 . . . . . . . . . . . . 0,02 | 0,0025 0,0016 0,0016 . . . . . . . . . . . . 0,0004 |
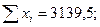
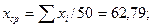
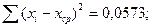
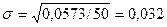 мм.
мм.
При малом количестве наблюдений (15—10 и меньше) вычисление 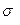 связано с большой ошибкой. Поэтому здесь приближенную оценку точности можно производить, определяя поле рассеяния, т. е. разность между наибольшей и наименьшей измеренными величинами.
связано с большой ошибкой. Поэтому здесь приближенную оценку точности можно производить, определяя поле рассеяния, т. е. разность между наибольшей и наименьшей измеренными величинами.
Пользуясь кривой распределения, можно найти вероятное количество годных деталей, на размер которых установлен определенный допуск. Предположим, что поле допуска 8 установлено двумя размерами х1 и х2 границ этого допуска от центра группирования (см. рис. 17, б). Вероятное количество годных деталей определяется в этом случае отношением заштрихованной площади Fl + F2 ковсей площади F, заключенной между кривой и осью абсцисс. С уменьшением допуска отношение площадей также уменьшается и вероятное количество годных деталей падает. При значительном (безграничном) расширении допуска отношение площадей приближается к единице. В этом предельном случае все детали становятся годными; математически это означает, что вероятность данного достоверного события равна единице.
Примем симметричное расположение кривой распределения относительно оси ординат. Тогда площадь Fг левого заштрихованного участка определится следующим образом:
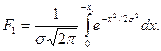 (13)
(13)
Площадь Fz правого заштрихованного участка найдется аналогичным путем:
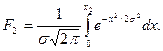 (14)
(14)
Эти интегралы обычно представляют в виде функции Ф (z), причем
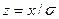 ;
;

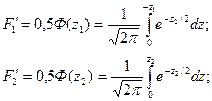 (15),(16)
(15),(16)
Величины F'1 и F'2 меньше единицы. Они выражают долю от всей площади между кривой Гаусса и осью абсцисс, принимаемой за единицу.
В табл. 2 приведены значения функции Ф (z) через десятую долю аргумента.
Таблица 2
Значения функции Ф(z)
| z | Ф(z) | z | Ф( z ) | z | Ф(z) |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 | 0,0000 0,0797 0,1585 0,2358 0,3108 0,3829 0,4515 0,5161 0,5763 0,6319 0,6827 0,7287 | 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 | 0,7699 0,8064 0,8385 0,8664 0,8904 0,9109 0,9281 0,9426 0,9545 0,9643 0,9722 0,9786 | 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 | 0,9836 0,9876 0,9907 0,9931 0,9949 0,9963 0,9973 0,99806 0,99862 0,99903 0,99933 0,99953 |
При z = ±3 функция Ф (z) = 0,9973. Это значит, что из всей партии деталей, обработанных данным методом, только 0,27% выходит запределы допуска х =6 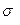 .
.
Вычислив по данным наблюдений значение 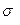 , можно охарактеризовать точность исследуемого технологического метода произведением 6
, можно охарактеризовать точность исследуемого технологического метода произведением 6 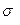 . В этом случае мы имеем практически 100-процентную годность обрабатываемых деталей, так как вероятное количество брака менее 0,3%. Величина 6
. В этом случае мы имеем практически 100-процентную годность обрабатываемых деталей, так как вероятное количество брака менее 0,3%. Величина 6 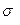 является условной. При 7
является условной. При 7 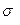 вероятное количество брака снижается очень мало. При 50 оно несколько возрастает. Правило «шести сигм» является достаточно простым, удобным и точным для практического пользования.
вероятное количество брака снижается очень мало. При 50 оно несколько возрастает. Правило «шести сигм» является достаточно простым, удобным и точным для практического пользования.
Описанный метод позволяет объективно оценить точность действующего процесса обработки, выполняемого при определенных условиях. При определении величины а, характеризующей точность данного метода, необходимо исключать при измерениях влияние систематической ошибки. В частности, для исключения погрешности формы цилиндрической поверхности, (представляющей в данном случае систематическую ошибку), измерения диаметральных размеров целесообразно производить в определенных сечениях у всех заготовок в партии.
Приведенные расчетные формулы позволяют решать многие задачи практического характера.
Пример 1. Определить вероятность получения брака деталей, если средне- квадратичное отклонение метода обработки 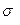 = 0,02 мм, а допуск на обработку
= 0,02 мм, а допуск на обработку 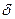 =0,08 мм. Границы поля допуска (рис. 17, б) расположены на расстояния!
=0,08 мм. Границы поля допуска (рис. 17, б) расположены на расстояния! 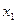 = 0,02 мм и
= 0,02 мм и 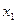 = 0,06 мм от центра группирования.
= 0,06 мм от центра группирования.
Решение. Найдем значения 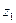 и
и  :
:
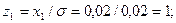
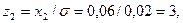
По табл. 2 определим F'1 и F'2:
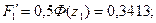
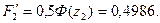
Вероятность получения брака W = 1 — 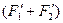 = 1 — (0,3413 + 0,4986) = 0,16.
= 1 — (0,3413 + 0,4986) = 0,16.
Пример 2.На сколько уменьшится вероятность получения брака по условиям предыдущей задачи, если центр группирования кривой распределения путем настройки технологической системы совместить с серединой поля допуска.
Решение. В данном случае
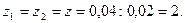
По табл. 2 найдём величины F'1 и F'2:
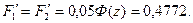
Вероятность получения брака
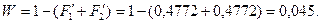
По сравнению с предыдущим случаем вероятность получения брака уменьшилась на 11,5%.
Кроме закона Гаусса встречаются и другие законы распределения размеров обработанных деталей в партии.
Если на выполняемый размер оказывает влияние систематическая равномерно возрастающая погрешность (погрешность, вызываемая размерным износом режущего инструмента и протекающим по закону прямой), то распределение происходит по закону равной вероятности (рис. 18, а). В верхней части рисунка показан рост погрешности к в зависимости от количества обработанных деталей п. Внизу дана соответствующая кривая распределения, имеющая вид прямоугольника.
Если на выполняемый размер влияет закономерно изменяющаяся погрешность, возрастающая сперва замедленно, а затем ускоренно (рис. 18 б, сверху), то распределение размеров происходит по з а к о н у треугольника (Симпсона). Кривая распределения показана в нижней части рисунка. Это распределение может иметь место при совместном действии размерного износа режущего инструмента с сильно выраженной фазой начального износа и увеличения силы резания в конце стойкости инструмента в результате его прогрессирующего затупления.
На рис. 18, в сверху показано изменение выполняемого размера х от времени обработки (количества обработанных деталей п) в результате тепловых деформаций технологической системы. Внизу дана соответствующая кривая распределения размеров.
При обработке заготовок методом пробных проходов кривая распределения действительных размеров получается несимметричной относительной поля допуска (рис. 18, г). Это обусловлено тем, что рабочий, производя пробные проходы и пробные промеры каждой заготовки, стремится держаться ближе к наибольшему предельному значению выполняемого размера (проходной стороне предельного калибра). При этом методе обработки влияние закономерно изменяющихся и систематических
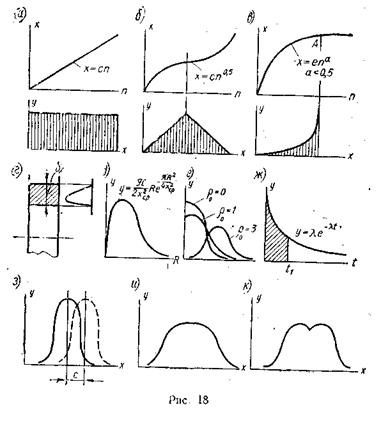
постоянных погрешностей значительно уменьшается и часто полностью отсутствует. Закон распределения приближается к закону Шарлье.
Рассмотрим теперь кривые распределения погрешностей взаимного положения и погрешностей формы поверхностей обработанных деталей. Эти погрешности являются существенно положительными величинами; они изменяются от нуля до определенного значения. Кривая распределения эксцентриситетов R ступенчатых цилиндрических деталей показана на рис. 18, д. Она имеет несимметричную форму. Характер изменения кривой говорит о том, что деталей с нулевым эксцентриситетом нет; большая часть деталей имеет средний по величине эксцентриситет; деталей с большим эксцентриситетом имеется мало. Закону эксцентриситета (закону Релея) следует также распределение значений непараллельности и неперпендикулярности двух плоскостей, неперпендикулярность оси детали к ее торцовой плоскости, разностенность полых деталей (при нефиксированной плоскости измерения). Этот закон однопараметрический. Среднее арифметическое значение *ср эксцентриситетов R связано со средним квадратичным отклонением постоянным соотношением
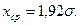
Закон распределения модуля разности к r двух случайных величин х1 и х2, распределение которых следует нормальному закону со средними значениями хср, и хсрг и средним квадратичным отклонением 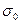 для величин r, выражает несимметричность поверхностей, непараллельность плоскостей, неперпендикулярности двух осей, овальность цилиндрической поверхности, отклонение шага резьбы и другие отклонения. Обозначив р =
для величин r, выражает несимметричность поверхностей, непараллельность плоскостей, неперпендикулярности двух осей, овальность цилиндрической поверхности, отклонение шага резьбы и другие отклонения. Обозначив р = 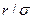 и р0 =
и р0 = 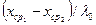 , можно написать уравнение кривой распределения
, можно написать уравнение кривой распределения
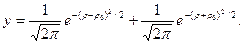 (17)
(17)
В зависимости от величины р0 имеем семейство кривых (рис. 18, e): при р0 = 1 получаем кривую распределения некруглости; при р0 = О кривая получается асимметричной; при р0 = 3 имеем кривую Гаусса. На рис. 18, ж показана кривая плотности вероятности отказов в работе собранного изделия или его элемента. По оси абсцисс отложено время t работы изделия (наработка на отказ). Кривая носит экспоненциальный характер и выражается уравнением
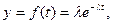 (18)
(18)
где 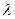 — интенсивность отказов (при экспоненциальной зависимости постоянна).
— интенсивность отказов (при экспоненциальной зависимости постоянна).
Вероятность отказа за время 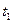 равна площади под кривой в интервале от 0 до
равна площади под кривой в интервале от 0 до 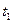 (заштрихованный участок). Вид кривой характеризует качество изделия с точки зрения надежности его работы.
(заштрихованный участок). Вид кривой характеризует качество изделия с точки зрения надежности его работы.
Систематическая постоянная погрешность не оказывает влияния на форму кривой распределения. Влияние этой погрешности сказывается лишь в том, что кривая распределения сдвигается на величину этой погрешности по оси абсцисс. На рис. 18, з сплошной линией показана кривая распределения, полученная при отсутствии систематической постоянной погрешности. Штриховой линией изображена кривая распределения, полученная после возникновения систематической погрешности. Данная кривая сдвинута вправо на величину с этой погрешности. Если наряду со случайными имеются и систематические закономерно изменяющиеся погрешности, то кривая распределения искажается. На рис. 18, и вкачестве примера показана кривая, представляющая собой композицию кривой Гаусса, и кривой равной вероятности. Эта кривая может получиться в том случае, когда на точность обработки оказывает сильное влияние размерный износ инструмента.
Кривая распределения для двух одинаковых партий деталей, обработка которых производилась при двух различных настройках станка, получается двухвершинной (рис. 18, к). Для нескольких настроек может получиться многовершинная кривая. При большом количестве настроек многовершинность сглаживается и кривая приобретает форму кривой нормального распределения, но с более широкой базой. Увеличение ширины базы происходит на величину погрешности настройки  .
.
Исследования показали, что распределение размеров деталей, обрабатываемых на предварительно настроенных станках, близко к нормальному. В технологических исследованиях, однако, часто возникает задача подбора теоретического закона на основе эмпирического распределения размеров. Самый простой и наглядный способ оценки близости эмпирического распределения размеров к подобранному теоретическому заключается в определении разности их ординат. Кривые должны при этом иметь одинаковые масштабы и одинаковые интервалы изменения частостей. Для суммарной оценки близости эмпирического распределения размеров к подобранному теоретическому закону используют критерии согласия Пирсона, В. И. Романовского и А. Н. Колмогорова. Определение и методика вычисления этих критериев приводятся в специальной литературе.
Статистический метод исследования на базе кривых распределения дает возможность объективно оценить точность различных способов механической обработки. Данный метод универсален. Его можно применить для исследования точности выполнения заготовок, сборочных операций, операций технического контроля, а также для целого ряда таких специфических операций, как балансировка, холодная правка и пр.
Единая методика, простота и несложные вычисления обусловили широкое применение этого метода для оценки точности самых различных технологических методов. Он особенно удобен (а часто и незаменим) в тех случаях, когда механизм явлений не изучен. Целесообразно применять его также для практической проверки результатов и выводов, полученных на основе расчетно-аналитического метода.
К существенным недостаткам данного метода относится, то, что он не вскрывает сущность физических явлений и факторов, влияющих на точность обработки, а также то, что на его базе не выявляются конкретные возможности повышения точности. Метод фиксирует результаты законченного этапа, т. е. «обращен в прошлое». Полученные ранее значения а не могут быть использованы, если в условиях выполнения данной операции произошли изменения (режим резания, способ установки заготовки и т. п.). В этом случае необходимо определить новое значение а.
Метод кривых распределения позволяет в ряде случаев выявить количественные и качественные зависимости точности от отдельных технологических факторов. Результаты исследования позволили, в частности, установить, что величина 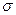
 практически не зависит от длины заготовок из проката, отрезаемых на станке с круглой пилой по упору. Этот вывод подтверждает аналитическое предположение об отсутствии влияния длины заготовки на ее допуск по длине.
практически не зависит от длины заготовок из проката, отрезаемых на станке с круглой пилой по упору. Этот вывод подтверждает аналитическое предположение об отсутствии влияния длины заготовки на ее допуск по длине.
Исследование точности выполнения отливок и штампованных заготовок методом кривых распределения позволило установить, что допуски на размеры отливок, получаемых в песчаных и постоянных формах, зависят не только от величины размеров, но и от направления размера по отношению к плоскости разъема формы. Размеры, перпендикулярные к плоскости разъема формы, выдерживаются с большими отклонениями, чем размеры, параллельные этой плоскости.
Исследования точности выполнения штампованных заготовок на молотах показали, что размеры, перпендикулярные к плоскости разъема штампов, выполняются также со значительно более широкими отклонениями, чем размеры параллельные этой плоскости.
Исследование процессов обработки методом кривых распределения позволяет объективно оценить точность выполнения данной технологической операции. Этот метод, однако, обладает тем недостатком, что при его использовании не учитывается последовательность обработки заготовок. Вся совокупность измерений рассматривается безотносительно к тому, какая деталь обработана раньше, какая позже. Кроме того, кривые распределения не дают возможности распознать каждую из причин, влияющих на результаты процесса. Построением и анализом кривых распределения можно выявить постоянную систематическую погрешность, которая определяется величиной имеющегося смещения центра группирования кривой для данной совокупности. Влияние закономерно изменяющихся систематических погрешностей может быть выявлено по характерному искажению формы кривой распределения. Выше отмечалось, что при интенсивном размерном износе режущего инструмента кривая Гаусса искажается и принимает форму плосковершинной кривой. Если, однако, по результатам измерений строится не кривая распределения, а непосредственно вычисляется среднее квадратичное отклонение, то систематически закономерно изменяющиеся погрешности не отделяются от случайных. В этом случае возможности данного метода в смысле выявления и устранения причин, обусловливающих те или иные погрешности, значительно уменьшаются.
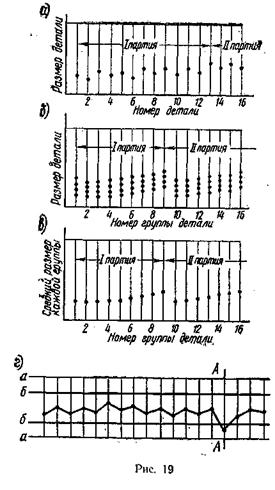
Точечныедиаграммы и их применение для исследования точности обработки. Другой метод исследования точности основан на построении точечных диаграмм. По горизонтальной оси откладывают номера обрабатываемых деталей в той последовательности, как они сходят со станка. По вертикальной оси в виде точек откладывают результаты измерений деталей. Подобные диаграммы можно строить как для одной так и для нескольких последовательно обрабатываемых партий деталей (рис. 19, а).
Длину подобных диаграмм можно значительно сократить, если по горизонтальной оси откладывать не номера заготовок, а номера групп деталей, причем в каждую группу входит одинаковое количество последовательно снимаемых со станка деталей (рис. 19, б).
На рис. 19, в показана диаграмма, по вертикальной оси которой откладываются средние арифметические значения размеров деталей, входящих в каждую группу. В данном случае гораздо легче уловить общую тенденцию изменения выполняемых размеров с течением времени. На рис. 19, вотчетливо видна периодичность изменения размеров в результате непрерывно протекающего износа режущего инструмента и периодически производимых поднастроек станка.
Свойства точечных диаграмм стали подробно изучать в связи с развитием и применением в промышленности статистического метода контроля продукции. Сущность этого метода заключается в том, что в процессе изготовления данной продукции периодически берут пробы в. количестве от двух до десяти деталей. Результаты измерений этих деталей, производимых универсальными инструментами, немедленно обрабатывают и наносят на специальную (контрольную) диаграмму. На этой диаграмме предусмотрены параллельные прямые а и а, определяющие границы поля допуска, и прямые б и б, определяющие поле рассеяния средних групповых значений и называющиеся контрольными прямыми.
Место контрольных прямых находят на основе теоретических положений статистического контроля, рассматриваемых в специальных курсах и литературе. На рис. 19, г в качестве примера показан образец диаграммы с нанесенными результатами контроля. Точки, соответствующие средним групповым значениям, соединены линиями. Вначале процесс обработки протекает нормально и ломанная линия не выходит за пределы контрольных прямых. При контроле группы А установлен выход ломаной линии за пределы контрольных границ. Это служит сигналом для поднастройки станка регулированием, или сменой инструмента, или проверкой положения упоров.
На контрольные диаграммы можно наносить не только средние групповые значения, но и другие параметры, характеризующие стабильность процесса обработки. К их числу можно отнести величину поля рассеяния, которая определяется по каждой группе измерений как разность предельных значений.
В последнее время обращается внимание на механизацию статистического контроля, которая достигается применением комбинированных приборов, производящих измерение размеров и фиксацию их величины на контрольную ленту. Кроме этого, известно применение приборов, которые производят измерение и усреднение результатов измерения. Последнее производят суммирующим устройством с электрическими или пневматическими датчиками. На этих приборах выполняют последовательное или одновременное измерение всех деталей, входящих в группу. В автоматизированных производствах находят применение устройства, автоматически управляющие процессом обработки на основе результатов измерения и их преобразования в статистические характеристики.
|
Применением статистического контроля предупреждается брак, так как контролируется не вся совокупность уже изготовленных деталей (как при обычных способах контроля), а правильность выполнения самого технологического процесса; при обнаружении отклонения своевременно применяют меры для и& устранения. При статистическом контроле значительно сокращается количество контролеров, так как выборочной проверке подвергается только 5—10% продукции.
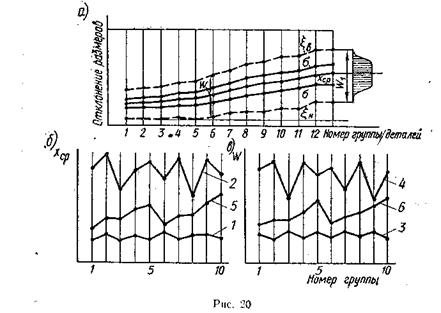
Метод точечных диаграмм в несколько измененном виде позволяет более четко выявить влияние систематических закономерно изменяющихся погрешностей на общую погрешность обработки. На рис.20, а показан пример так называемой т о ч н о с т н о и диаграммы.
Для каждой группы последовательно обработанных деталей находят: среднее арифметическое xср и среднее квадратичное 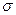 отклонения, а также предельные верхнее
отклонения, а также предельные верхнее 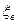 и нижнее
и нижнее 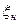 отклонения от средней арифметической величины (разность этих отклонений есть поле рассеяния W для каждой группы). Количество деталей в каждой группе рекомендуется брать равным 25, а если обрабатывается большая партия изделий (более 300 шт.) то и большим. При размере партии, например, в 300 шт. общее количество групп составляет 12. Если размер партии исчисляется несколькими тысячами штук, то измерения деталей нужно делать в порядке их изготовления, но группы берут не подряд, а через равные количества неизмеряемых деталей.
отклонения от средней арифметической величины (разность этих отклонений есть поле рассеяния W для каждой группы). Количество деталей в каждой группе рекомендуется брать равным 25, а если обрабатывается большая партия изделий (более 300 шт.) то и большим. При размере партии, например, в 300 шт. общее количество групп составляет 12. Если размер партии исчисляется несколькими тысячами штук, то измерения деталей нужно делать в порядке их изготовления, но группы берут не подряд, а через равные количества неизмеряемых деталей.
В показанной на рис. 20, а точностной диаграмме по оси абсцисс отложены номера последовательно взятых групп, а по оси ординат — вычисленные значения 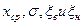 . Соединяя полученные точки ломаными линиями, мы получаем характеристику изменения указанных величин во времени протекания исследуемого процесса обработки. Проведя аналогичные наблюдения по нескольким партиям, можно получить более сглаженную диаграмму. Скачки, вызванные сменой или подналадкой режущего инструмента (или другими причинами), учитывают путем совмещения границы ближайшей группы с местом скачка. Из диаграммы видно, что поля рассеяния W и
. Соединяя полученные точки ломаными линиями, мы получаем характеристику изменения указанных величин во времени протекания исследуемого процесса обработки. Проведя аналогичные наблюдения по нескольким партиям, можно получить более сглаженную диаграмму. Скачки, вызванные сменой или подналадкой режущего инструмента (или другими причинами), учитывают путем совмещения границы ближайшей группы с местом скачка. Из диаграммы видно, что поля рассеяния W и 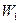 размеров в пределах отдельных групп различны; они меньше поля рассеяния всей совокупности деталей.
размеров в пределах отдельных групп различны; они меньше поля рассеяния всей совокупности деталей.
Если распределение размеров в пределах одной группы отвечает нормальному закону, то для всей совокупности деталей, оно может отличаться от этого закона в силу большего или меньшего влияния систематической закономерности изменяющейся погрешности. Так, например, при изменении хср по закону прямой, наклоненной под углом к оси абсцисс (размерный износ инструмента), распределение размеров деталей во всей совокупности будет характеризоваться плосковершинной кривой.
Наличие нескольких систематических факторов с постоянной и переменной интенсивностью их действия во времени приводит к целому семейству теоретических кривых распределения, подробно рассмотренных Н. А. Бородачевым.
Установив на точностной диаграмме положение кривой, характеризующей изменение xср для отдельных групп во времени, можно выявить влияние систематических закономерно изменяющихся погрешностей на общую погрешность обработки. Если, например, значения xср расположены на прямой, наклоненной к оси абсцисс под некоторым углом, то величина систематической погрешности выражается уравнением прямой с соответствующим угловым коэффициентом. Величина систематической погрешности может быть дана в функции времени или количестве снятых со станка деталей. Можно ее выражать также в функции обработанной поверхности или длины пути инструмента в металле обрабатываемых заготовок. При распределении значений ,vcp по параболе величина систематической погрешности может быть выражена уравнением кривой второго порядка. В более сложных случаях зависимость целесообразно представлять аппроксимирующейся функцией.
К недостатку данного метода исследования точности нужно отнести то, что при наличии нескольких закономерно изменяющихся систематических погрешностей они не разделяются, а их влияние на суммарную погрешность оценивается комплексно. Кроме того, для исследования необходимо большое количество наблюдений.
Точностные диаграммы позволяют оценить технологические процессы во времени их протекания по устойчивости и стабильности признаков качества производимой продукции. Устойчивость характеризует во времени постоянство величины хср, стабильность — поля рассеяния W.
На рис. 20, б и в показаны типовые кривые изменения во времени величин xср и W. Кривые 1 и 3 представляют устойчивый и стабильный технологический процесс; кривые 1 и 4—устойчивый, но нестабильный процесс с большим полем рассеяния W; кривые 2 и 3—неустойчивый, но стабильный процесс; кривые 2 и 4—неустойчивый и нестабильный процесс. Кривые 5 и 6 соответственно представляют циклически устойчивый и циклически стабильный процессы; в обоих случаях изменения величин xср и W происходят периодически по определенному закону. Объективную оценку устойчивости и стабильности производят сопоставляя амплитуды изменения величин хср и W с полем допуска 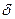 . Устойчивость и стабильность технологического процесса считают достаточной, если амплитуда изменения указанных величин меньше (0,4—0,5)
. Устойчивость и стабильность технологического процесса считают достаточной, если амплитуда изменения указанных величин меньше (0,4—0,5) 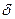 . В отдельных случаях требования к устойчивости и стабильности могут быть выше.
. В отдельных случаях требования к устойчивости и стабильности могут быть выше.
10. Точность и погрешность обработки детали.
Любой процесс сопровождается действием большого количества случайных факторов, которые вызывают отклонения показателей качества и количества изделий, выпущенных в единицу времени, и их стоимости от стоимости расчетных значений. То есть, между расчетными и действительными результатами процесса всегда бывают расхождения. К тому же, определить действительные результаты можно с ошибками. Поэтому различают три вида значений любого показателя: номинальное или теоретическое (расчетное); действительное (объективно существующее); измеренное, то есть действительное значение, познанное с каким-то отклонением.
Под точностью показателя понимают степень приближения действительного значения показателя к его номинальному значению.
Нельзя достичь абсолютной точности показателей, поэтому на отклонения показателей от идеала налагают ограничения. Границы допустимых отклонений показателя, предопределяемые требованиями к качеству, количеству или стоимости производимых изделий называются допуском. Допуск устанавливается в соответствии со служебным назначением изделия, (то есть потребности человека).
Говоря о точности, различают требуемую (расчетную) и фактическую (познанную).
Сопоставление фактической и требуемой точности векторной величины может быть проведено наложением границ рассеяния значений вектора на границе допуска, заданного частью n-мерного пространства.
Машина считается качественной при полном соответствии фактической точности показателей требуемой, то есть:
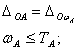
Показатели качества машины (производительность, мощность, КПД, долговечность и другие) обеспечиваются в конструкции машины связями свойств материалов деталей и размерными связями, поэтому при изготовлении машины необходимо обеспечить соответствие фактической точности требуемой и свойств материалов, и размерных связей.
Представление о геометрическом образе детали дают форма и размеры поверхностей, расстояние между ними и их относительное угловое положение. Поэтому точность геометрического образа детали характеризуется тремя показателями.
1) Точность размеров и расстояний ( 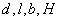 )
)
2) Точность относительного поворота (перпендикулярность и параллельность)
3) Точность формы:
а) макроотклонения – отклонения реальной поверхности от правильной геометрической формы в пределах ее габаритных размеров;
б) волнистость - периодические неровности поверхности, встречающиеся на участках протяженностью от 1 до 10 мм;
в) микроотклонения – микронеровности на участках протяженностью до 1мм называются шероховатостью.
Между значениями отклонений всех трех показателей существуют качественные и количественные связи
Под погрешностью обработки понимают отклонение полученного при обработке значения геометрического или другого параметра от заданного. Абсолютную погрешность выражают в единицах рассматриваемого параметра: 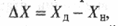 где
где 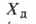 и
и 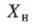 — соответственно действительное (полученное) и номинальное значения параметра. При несимметричном расположении поля допуска относительно номинального значения вместо номинального значения параметра принимают его среднее значение. Отношение абсолютной погрешности к заданному значению параметра называют относительной погрешностью:
— соответственно действительное (полученное) и номинальное значения параметра. При несимметричном расположении поля допуска относительно номинального значения вместо номинального значения параметра принимают его среднее значение. Отношение абсолютной погрешности к заданному значению параметра называют относительной погрешностью:
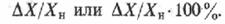
Количественно точность характеризуется обратной величиной модуля относительной погрешности
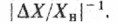
Конструктивные допуски и технические требования на изготовление деталей назначают с учетом условий работы деталей в машине. Эти требования обеспечиваются финишными переходами обработки. Однако важно обязательное соблюдение технологического регламента изготовления детали и на всех предшествующих переходах обработки, так как результаты финишных переходов обработки существенно зависят от качества выполнения предшествующих переходов обработки.
Дата добавления: 2015-04-16; просмотров: 1594; Мы поможем в написании вашей работы!; Нарушение авторских прав |