УЧЕТ ФЛУКТУАЦИЙ АМПЛИТУДЫ И ФАЗЫ ПРИ ВЫПОЛНЕНИИ ОПЕРАЦИЙ ДИФЕРЕНЦИРОВАНИЯ И ИНТЕГРИРОВАНИЯ

Флуктуации амплитуды и фазы напряжения и тока в электрической цепи необ­ходимо учитывать при выполнении операций дифференцирования и ин­тегрирования. Пусть, например,

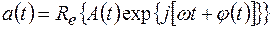(2.16)

В случае, когда или , т.е. амплитуда и фаза постоянны, первая производная имеет вид:

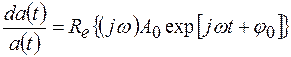(2.17)

Собственно n~ая производная,равна

(2.18)

Из рассмотрения выражений (2.17) и (2.18) видно, что операция дифференцирования эквивалентна умножению исходного выражения ( 2.16) на «jw».

Аналогично оказывается, что операция интегрирования эквивалентна делению выражения (2.16.) на «jw».

Соотношения (2.17), (2.18) положены в основе широко применяемого символического метода расчета электрических цепей

При анализе или синтезе реальных электрических и электронных цепей с учетом флуктуаций амплитуды и фазы напряжения производную по времени от выражения (2.I6.) необходимо представлять в следующем виде:

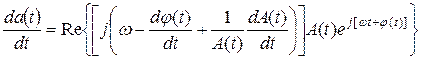(2.19)

Соответственно n-ая производная по аналогии с (2.19) принимает вид:

(2.20)

Как следует из выражений (2.19) и(2.20), оператор « jw « , используемый при символическом методе, следует везде заменить на оператор:

. (2.21.)