
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Анализ цепи переменного тока с индуктивным сопротивлением.
Пусть имеется электрическая цепь переменного тока с потребителем, содержащим только одну индуктивность L (рис. 11).
Активное сопротивление цепи R и емкость C будем считать равными нулю, а L = const. Это будет идеальная цепь, так как любой потребитель имеет также активное сопротивление и емкость.
Практически потребителем с чистой индуктивностью может быть катушка, состоящая из большого числа витков проволоки с большим поперечным сечением и малым удельным сопротивлением. Если бы такая катушка была включена в цепь постоянного тока, то ток в ней был бы весьма большим, так как при R ≈ 0 имелось бы фактически короткое замыкание. При включении индуктивной катушки в цепь переменного тока такого явления не наблюдается, так как ток в ней при значительном числе витков обычно не достигает больших значений. Указанное обстоятельство объясняется тем, что при изменении тока в цепи по величине и направлению изменяется создаваемый током магнитный поток, пронизывающий катушку (сцепленный с проводниками катушки). Циклически изменяющийся магнитный поток вызывает появление в катушке э.д.с. самоиндукции, которая во время возрастания тока направлена против него, а при убывании тока имеет одинаковое с ним направление. Таким образом, э.д.с. самоиндукции в соответствии с законом Ленца препятствует как увеличению, так и уменьшению тока. Как будет показано далее, результирующее действие э.д.с. самоиндукции, препятствующей всем изменениям тока, в конечном итоге ограничивает величину амплитуды, а следовательно, и действующее значение тока. Таким образом, индуктивность в цепи оказывает дополнительное препятствие (сопротивление) для прохождения переменного тока, называемое индуктивным сопротивлением.
Индуктивность в цепях постоянного тока может проявляться только в нестационарных режимах (т.е. при включении, отключении и всяких изменениях тока по величине).
К индуктивным сопротивлениям относят катушки со стальным сердечником (и без него), имеющие большое число витков проволоки. При этом иногда полностью пренебрегают их активным сопротивлением. Индуктивными сопротивлениями обладают такие части аппаратов, приборов и машин, в которых при прохождении тока создаются большие магнитные потоки (например, обмотки электродвигателей, генераторов, трансформаторов, катушки контакторов и реле и т.д.).
Пусть к катушке индуктивности L, для которой  (рис. 1-7, а), приложено синусоидальное напряжение и:
(рис. 1-7, а), приложено синусоидальное напряжение и:

При установившемся режиме протекающий через катушку переменный ток i создаст на ее обмотке переменную ЭДС самоиндукции  Тогда в соответствии со вторым законом Кирхгофа для такой цепи можно записать:
Тогда в соответствии со вторым законом Кирхгофа для такой цепи можно записать:

Выясним форму установившегося тока, соотношение фаз тока и напряжения и закон изменения мощности.
Значение ЭДС самоиндукции, как известно, можно записать так:

откуда с учетом уравнения (1.11) имеем:

Проинтегрируем последнее уравнение и получим:

где A — постоянная интегрирования  при отсутствии постоянной составляющей тока в данной цепи). Кроме того, при
при отсутствии постоянной составляющей тока в данной цепи). Кроме того, при
 ток i становится максимальным:
ток i становится максимальным:

Окончательно имеем:

Сравнивая соотношения (1.10) и (1.13), видим, что ток i в катушке также синусоидальный. Одиако, имея одинаковую частоту, ток отстает по фазе от приложенного напряжения на четверть периода, т. е. на 
Векторная и временная диаграммы для цепи переменного тока с индуктивностью изображены на рисунках 1-7, б и 1-7, в соответственно.
Деля соотношение (1.12) на  получим:
получим:

Здесь  имеет размерность сопротивления и называется индуктивным сопротивлением, обозначается:
имеет размерность сопротивления и называется индуктивным сопротивлением, обозначается:  .
.
Соотношение  представляет собой математическую запись закона Ома для цепи переменного тока с индуктивностью.
представляет собой математическую запись закона Ома для цепи переменного тока с индуктивностью.
Найдем выражения для мгновенной и средней (активной) мощности в случае чисто индуктивной цепи.
Мгновенная мощность

изменяется по закону синуса с удвоенной частотой (рис. 1-8).

Рис. 1-8
При этом положительные значения мощности (четные четверти периода) соответствуют потреблению энергии катушкой (энергия запасается магнитным полем катушки), отрицательные значения мощности соответствуют возврату запасенной энергии обратно источнику.
Средняя за период мощность (активная мощность) в этой цепи равна нулю:

Индуктивность вызывает лишь «перекачивание» электрической энергии по проводам от источника (когда ток и напряжение на графике имеют одинаковые знаки) и обратно (ток и напряжение имеют разные знаки).
20. Анализ цепи переменного тока с ёмкостным сопротивлением.
Как известно из курса физики, совокупность двух проводников, разделенных слоем диэлектрика, называется конденсатором и представляет собой электрическую емкость.
Следовательно, всякая электрическая линия передачи (воздушная или кабельная) может рассматриваться как некоторая система конденсаторов или емкость.
Особенно большой емкостью обладают кабельные линии. Если приложить к кабелю периодически изменяющееся напряжение и оставить разомкнутым все его жилы в конце линии, то в кабеле, при его значительной длине, будут непрерывно циркулировать зарядно-разрядные токи.
При понижении напряжения заряды будут стекать с обкладок обратно к генератору.
Под влиянием сил переменного электрического поля между обкладками конденсатора в атомах диэлектрика происходит смещение электронов то в одну, то в другую сторону. Это направленное колебательное движение электронов в атомах диэлектрика представляет собой так называемый ток смещения.
Таким образом, в проводах, соединяющих генератор с конденсатором, будут циркулировать зарядный и разрядный токи проводимости, а в диэлектрике между обкладками конденсатора – токи смещения. Поэтому принято считать, что конденсатор как бы «пропускает» через себя переменный электрический ток.
Пусть к обкладкам конденсатора емкостью С (рис. 1-12, а) приложено синусоидальное напряжение  . Активным и индуктивным сопротивлениями этой цепи пренебрежем, считая
. Активным и индуктивным сопротивлениями этой цепи пренебрежем, считая  . Тогда при установившемся режиме через конденсатор С, как известно, будет протекать некоторый переменный ток t. Выясним форму и определим фазу этого тока и сравним их соответственно с формой и фазой приложенного напряжения и.
. Тогда при установившемся режиме через конденсатор С, как известно, будет протекать некоторый переменный ток t. Выясним форму и определим фазу этого тока и сравним их соответственно с формой и фазой приложенного напряжения и.
Мгновенное значение тока в цепи с емкостью представим равным скорости изменения электрического заряда q на обкладках конденсатора
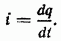
Так как  и в любой момент времени напряжение на обкладках конденсатора уравновешивается приложенным напряжением и, то
и в любой момент времени напряжение на обкладках конденсатора уравновешивается приложенным напряжением и, то
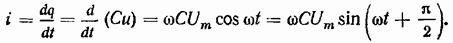
При  ток i становится максимальным:
ток i становится максимальным:

тогда
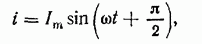
т. e. ток, как и приложенное напряжение, изменяется по закону синуса,  опережает его по фазе на
опережает его по фазе на 
Векторная и временная диаграммы для цепи переменного тока с емкостью приведены на рисунках 1-12, б и 1-12, в соответственно.

Рис. 1-13
Деля соотношение (1.22) на  получим:
получим:

здесь — имеет размерность сопротивления и называется емкостным сопротивлением, обозначается 
Соотношение  представляет собой математическую запись закона Ома для цепи переменного тока с емкостью.
представляет собой математическую запись закона Ома для цепи переменного тока с емкостью.
Найдем выражения для мгновенной и средней (активной) мощности в случае чисто емкостной цепи.
Мгновенная мощность

изменяется по закону синуса с удвоенной частотой (рис. 1-13). При этом положительные значения мощности (нечетные четверти периода) соответствуют потреблению энергии конденсатором (энергия запасаетсяэлектрическим полем конденсатора), отрицательные значения соответствуют возврату запасенной энергии обратно источнику.
Средняя за период мощность (активная) в этой цепи равна нулю:

т. e. в идеализированной цепи переменного тока с конденсатором происходит лишь периодический обмен электрической энергией между источником и этим конденсатором.
Дата добавления: 2015-04-16; просмотров: 390; Мы поможем в написании вашей работы!; Нарушение авторских прав |