Анализ цепи переменного тока с параллельным соединением двух катушек индуктивности.

Параллельное соединение двух катушек индуктивности - раздел Философия, Расчет цепей переменного тока с последовательным соединением элементов ...

Расчет производится на основании построения векторной диаграммы, при ее построении начальная фаза напряжения (α0i) выбирается равной 0. В цепях с катушками вектора токов будут отставать от напряжения на углы φ1 и φ2.

Токи в ветвях рассчитываются по формулам:

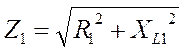
Для определения величины общего тока I, можно воспользоваться несколькими способами:

а) Графически, построив в масштабе векторную диаграмму;

б) Аналитически (используя теорему косинусов):

в) Методом треугольника токов:

Каждый ток раскладывается на активную составляющую (Ia) и реактивную составляющую (Iр)

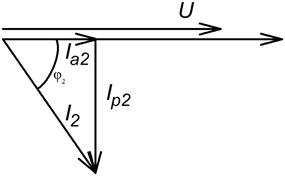
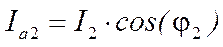
Для нахождения общего тока нужно сложить вектора и

Для определения величины общего тока вектора переставляются таким образом, чтобы активные части токов составляли один катет треугольника, а реактивные части второй катет. Общий ток – гипотенуза.

Определить величину общего тока можно используя теорему Пифагора:

г) Метод проводимостей:

Находим активную (g), реактивную (b) и полную (y) проводимость ветвей:

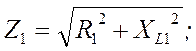
Находим эквивалентную проводимость цепи:

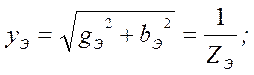
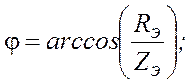
25. Анализ цепи переменного тока с параллельным соединением активного и ёмкостного сопротивлений.

См конспект

26. Анализ цепи переменного тока с параллельным соединением активного, индуктивного и ёмкостного сопротивлений.

Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов (рис. 2.31, а).

Требуется по известным G, ВL, ВC, U рассчитать токи. Как и прежде, задачу будем решать двумя методами.

1. М е т о д в е к т о р н ы х д и а г р а м м.

Токи ветвей находятся сразу: , , .

Для определения общего тока 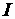необходимо построить векторную диаграмму (рис. 2.31, б). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей. Из векторной диаграммы имеем

или ,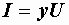

где 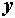– полная проводимость цепи, равная

.

Разность индуктивной и емкостной проводимостей представляет собой общую реактивную проводимость цепи .

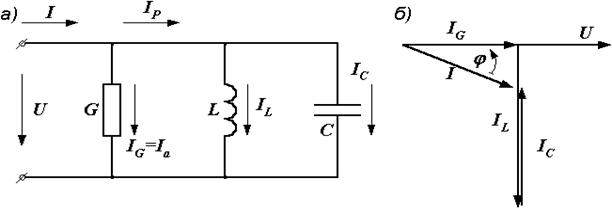
Рис. 2.31. Электрическая цепь и ее векторная диаграмма

Векторы токов на диаграмме образуют треугольник токов. Его горизонтальный катет, представляющий проекцию вектора тока на вектор напряжения, называется активной составляющей тока и равен току в активном элементе цепи: 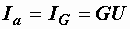(рис. 2.32, а). Проекция вектора тока на направление, перпендикулярное напряжению, – это реактивная составляющая тока. Она равна суммарному току реактивных элементов 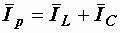и определяется как разность длин векторов:

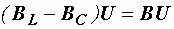(см. рис. 2.31, б и 2.32, а).

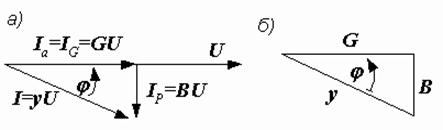
Рис. 2.32. Треугольники токов и проводимостей

Разделив все стороны треугольника токов на , получим треугольник проводимостей (рис. 2.32, б), стороны которого связаны следующими соотношениями:

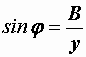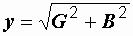, , , . (2.29)

2. С и м в о л и ч е с к и й м е т о д.

Раньше были получены следующие формулы:

, , .

Подставляя их в уравнение первого закона Кирхгофа, получаем:

или ,

где – комплексная проводимость цепи, равная

Пример 2.12. Для цепи, показанной на рис. 2.33, а, рассчитать токи, угол сдвига фаз между током и напряжением на входе цепи, построить векторную диаграмму. Числовые значения параметров цепи: 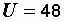В, Ом, мкФ, с-1.

Рис. 2.33. Электрическая цепь и ее векторная диаграмма

Р е ш е н и е.

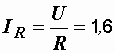А, Ом,

А, А.

Векторная диаграмма приведена на рис. 2.33, б.

Угол сдвига фаз .

Величину общего тока можно найти иначе:

См, См,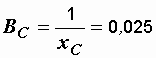

См, А.

Пример 2.13. Начертить цепь, векторная диаграмма которой изображена на рис. 2.34, а.

Р е ш е н и е задачи показано на рис. 2.34, б.

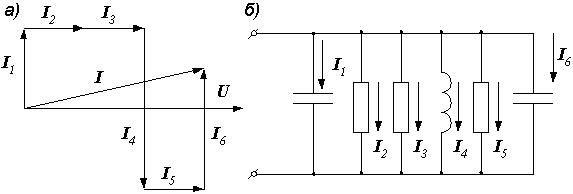
Рис. 2.34. Векторная диаграмма и соответствующая ей электрическая цепь

Пример 2.14. Чему равно показание амперметра А на входе цепи в схемах рис. 2.35, если амперметры А1 и А2 во всех случаях показывают соответственно 4 и 3 А?

Рис. 2.35. Измерение тока в электрической цепи

Предлагаем для каждого случая самостоятельно построить векторную диаграмму и убедиться в правильности приведенных ответов: а) 5А, б) 7А, в) 1А.

27.Резонанс токов: условие его возникновения, особенности.

Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.

Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.

Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.

Выразим резонансную частоту

Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.

Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.