Анализ цепи переменного тока с активно-индуктивным сопротивлением.

Рассмотрим цепь переменного тока, состоящую из активного сопротивления R и катушки индуктивности L, соединенных последовательно (рис. 1-9, а). Такая цепь имеет существенное значение для выяснения зависимости сдвига фаз между током и напряжением от соотношения значений R и L. Кроме того, все реальные цепи, содержащие индуктивность, имеют и активное сопротивление сопротивление провода обмотки и подводящих проводов, потери в сердечниках и т. д.). Для такой цепи условие электрического равновесия (по второму закону Кирхгофа) можно записать в следующем виде:

т. е. приложенное напряжение и уравновешивается суммой «ал-ря-жений на элементах цепи R и L.

Предположим, что в рассматриваемой цепи установился синусоидальный ток:

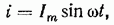
тогда напряжения на элементах R и L будут равны:

а приложенное напряжение

Рис. 1-9

Полученный результат (1.18) показывает, что. приложенное напряжение и также синусоидально, т. е. наше допущение (1.16) верно. Для нахождения

окончательного уравнения приложенного напряжения, которое может обеспечить предполагаемый нами ток i в цепи, построим в соответствии с соотношениями (1.16) и (1.17) векторную диаграмму (рис. 1-9, б), на которой найдем вектор приложенного напряжения

Из полученной векторной диаграммы следует, что в рассматриваемой цепи ток отстает по фазе от приложенного напряжения U, но не на как в случае чистой индуктивности, а на некоторый угол Причем, и при заданной индуктивности зависит в конечном счете от значения активного сопротивления: угол уменьшается с увеличением

Таким образом, для рассматриваемой цепи приложенное напряжение и следует представить в виде

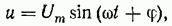
где (из векторной диаграммы).

Временные диаграммы тока и напряжений в цепи с R и L представлены на рисунке 1-9, в.

На векторной диаграмме (рис. 1-9, б) векторы образуют так называемый треугольник напряжений. Если все стороны этого треугольника разделить на значение тока в цепи то получится треугольник, подобный данному, — треугольник сопротивлений (рис. 1-10). Стороны этого треугольника не являются векторами. Это отрезки, так как сопротивления постоянны и не изменяются гармонически подобно току или напряжению.

Из треугольника сопротивлений (см. рис. 1-10) имеем:

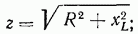
где z — полное, R — активное и индуктивное сопротивление.

Тогда закон Ома для цепи с активным и индуктивным сопротивлениями можно представить в виде

Теперь определим угол из соотношения

Выясним, как изменяется мощность в цепи с R и L. Поскольку мгновенные значения можно представить как

Рис. 1-10

то мгновенное значение мощности равно

Как видно, мгновенное значение мощности имеет две составляющие: активную и индуктивную причем обе составляющие зависят от угла сдвига фаз между током и напряжением. Так, в случае цепь становится чисто активной (см. рис. 1-6) и мгновенная мощность равна

а в случае чисто индуктивной (см. рис. 1-8).

Временную диаграмму мгновенной мощности можно построить, перемножая ординаты соответствующих диаграмм тока и напряжения для каждого момента времени (рис. 1-11).

В случае средняя за период мощность не равна нулю:

и представляет собой активную мощность. Соответствующая этой мощности электрическая энергия поступает от источника и превращается в активном сопротивлении R, например, в теплоту. В самом деле, подставив в формулу (1.21) значение из соотношения (1.20), получим:

Рис. 1-11

Рис. 1-12

Среднее же значение реактивной (индуктивной) составляющей мощности равно нулю:

Итак, в цепи переменного тока с R и L угол сдвига фаз между током и напряжением зависит от соотношения значений R и L и изменяется в пределах

22. Анализ цепи переменного тока с активно-ёмкостным сопротивлением.

В реальных цепях переменного тока с емкостью всегда имеется активное сопротивление (сопротивление проводов, активные потери в конденсаторе и т. д.). Поэтому реальную цепь с емкостью следует рассматривать состоящей из последовательно соединенных активного сопротивления R и конденсатора С (рис. 1-14, а).

Рис. 1-14

Для такой цепи уравнение электрического равновесия в соответствии со вторым законом Кирхгофа можно записать так:

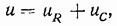
т. е. приложенное напряжение и уравновешивается суммой напряжений на элементах цепи R и С соответственно.

Если установившийся ток i в цепи принять равным напряжения на элементах R и С этой цепи будут равны

Интегрируя уравнение (1.26), получим:

Здесь A = 0 (постоянная интегрирования). При синусоидальном токе напряжение на конденсаторе также синусоидально. При имеем:

Окончательно:

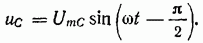
Подставим соотношения (1.26) и (1.27) в условие электрического равновесия (1.23):

Следовательно, приложенное напряжение и является также синусоидальным, поэтому допущение (1.24) о синусоидальной форме тока является правильным.

Из векторной диаграммы (рис. 1-14, б) следует, что в рассматриваемой цепи ток опережает по фазе приложенное напряжение, но не на , как в случае чистой емкости, а на некоторый угол причем и при заданной емкости С зависит от значения активного сопротивления R (угол уменьшается с увеличением R).

Таким образом, для рассматриваемой цепи приложенное напряжение можно представить в виде

где (из векторной диаграммы).

Временные диаграммы тока и напряжений в цепи с R и С представлены на рисунке 1-14, в.

На векторной диаграмме (см. рис. 1-14, б) векторы образуют треугольник напряжений, из которого следует:

откуда

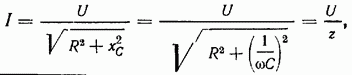
где полное сопротивление цепи с R и С, а выражение

представляет собой закон Ома для активно-индуктивной цепи.

Разделив стороны треугольника напряжений на значение тока в цепи получим треугольник сопротивлений, из которого найдем угол из соотношения

Для выяснения закона изменения мощности в цепи с R и С представим ток и напряжение в следующем виде:

тогда мгновенное значение мощности равно

Как видно, мгновенное значение мощности имеет две составляющие: активную и реактивную (емкостную) , причем обе составляющие зависят от угла сдвига между током и напряжением. Так, в случае цепь становится чисто активной (см. рис. 1-6):

Рис. 1-15

а в случае чисто емкостной (см. рис. 1-13):

Временную диаграмму мгновенной мощности можно построить, перемножая ординаты соответствующих диаграмм тока и напряжения для каждого момента времени (рис. 1-15). Когда средняя за период мощность (активная) не равна нулю; электрическая энергия при этом безвозвратно расходуется в активном сопротивлении

Среднее же значение реактивной (емкостной) составляющей мощности равно нулю:

Таким образом, в случае цепи переменного тока с R и С изменение значений R и С приводит к изменениямсдвига фаз в пределах

23. Анализ цепи переменного тока с последовательным соединением активного, индуктивного и ёмкостного сопротивления. Резонанс напряжений.

Рассмотрим цепь переменного тока (рис. 1-16), состоящую из последовательно соединенных R, L и С. Условие электрического равновесия для такой цепи следующее:

Полагая, что общий для всех элементов цепи ток i изменяется по закону синуса:

напряжения на элементах этой цепи будут соответственно равны

Для получения фазовых соотношений тока I и приложенного напряжения U построим векторную диаграмму (рис. 1-17, а), исходя из условия (1.28), записанного в векторной форме:

где

В результате построений получим треугольник напряжений, гипотенуза которого численно (в масштабе) равна приложенному напряжению U. При этом разность фаз определяется соотношением векторов . Так, при угол положителен (индуктивный характер нагрузки), при угол отрицателен (емкостный характер нагрузки) и при угол равен нулю (нагрузка становится чисто активной).

Деля стороны треугольника напряжений (см. рис. 1-17, а) на значение тока в цепи получим треугольник сопротивлений (рис. 1-18), в котором R — активное, реактивное полное сопротивление цепи. Из треугольника сопротивлений следует:

где

или

Кроме того,

Рис. 1-16

Рис. 1-17

Рис. 1-18

Рис. 1-1»

Закон Ома для цепи переменного тока, содержащей R, L и С, имеет вид

От треугольника напряжений легко перейти (умножением на значение тока I) к треугольнику мощностей (рис. 1-19). Здесь S — полная мощность, Q — реактивная составляющая мощности и Р — активная составляющая мощности.

Из треугольника мощностей следует:

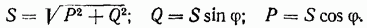
Так как то тогда

На практике широко используют следующие формулы:

Реактивная мощность Q всегда порождает наличие обменной энергии. Ее измеряют в вольт-амперах реактивных и киловольт-амперах реактивных .

Полную мощность S, содержащую в себе активную и реактивную мощности, иначе называют кажущейся, т. е. такой, которую может дать источник (генератор, трансформатор). При полная мощность 5 становится вся реактивной, а при активной, т. е. ее составляющие определяются характером нагрузки.

Единицами измерения полной мощности являются вольт-ампер (ВА) и киловольт-ампер . Эта мощность и указывается в паспортах генератора и трансформатора переменного тока.

Активная мощность Р соответствует электрической энергии, используемой для совершения механической работы, для получения теплоты и т. д. Она измеряется в ваттах и киловаттах

Активная мощность Р кроме тока и напряжения зависит еще и от с увеличением убывает и Р, а с уменьшением активная мощность Р возрастает. Поэтому множитель в

формуле (1.29) показывает, какую часть полной мощности безвозвратно расходует нагрузка. Этот множитель называют коэффициентом мощности.

Для более рационального использования мощности станции надо стремиться сделать нагрузку такой, чтобы Однако на практике в масштабе промышленного предприятия добиться этого весьма трудно, хотя часто значение доводят до 0,9-0,95. Низкие значения порождают значительные дополнительные потери на нагревание проводов обмоток генератора и линий электропередач. Покажем это.

Пусть одинаковые активные мощности передаются к двум равным нагрузкам с , т. е.

Приравняв получим:

Мощность расходуемая на нагревание проводов в цепи с равна

а мощность расходуемая на нагревание таких же проводов, но с равна

т. e. потери на нагревание проводов обратно пропорциональны квадрату коэффициента мощности. Этого и следовало ожидать, так как реактивная мощность (она велика при низких создает в проводах дополнительный реактивный ток, а потери на теплоту пропорциональны квадрату тока.

Повышение является задачей государственной важности. Так, повышение в энергосистемах Советского Союза всего лишь на 0,01 может дать экономию электроэнергии более 500 млн. кВт-ч в год (годовое производство Волжской ГЭС им. В. И. Ленина).

РЕЗОНАНС НАПРЯЖЕНИЙ

В последовательной цепи с R, L и С (см. рис. 1-16) приложенное напряжение U равно сумме падений напряжений на активном сопротивлении, индуктивности и емкости. Векторная диаграмма такой цепи изображена на рисунке 1-17, в, из которой находим

Обозначив полное сопротивление цепи через :

можно записать закон Ома для данной цепи:

В рассматриваемой цепи при нагрузка является активно-индуктивной, а при активно-емкостной.

Важным является случай, когда . Тогда ток в цепи равен

т, е. цепь в данном случае имеет наименьшее возможное сопротивление, как будто в нее включено только активное сопротивление . При этом напряжения на индуктивности и емкости сдвинутые по фазе на , полностью компенсируют друг друга (рис. 1-17, в). Напряжение, приложенное к цепи, равно напряжению на активном сопротивлении, и ток совпадает по фазе с напряжением. Этот случай получил название резонанса напряжений.

Итак, условием резонанса напряжений является равенство индуктивного и емкостного сопротивлений цепи:

Явление резонанса напряжений имеет важное значение для практики.

Прежде всего, если в цепь с индуктивностью включить последовательно переменную емкость и постепенно изменять ее, например увеличивая, то ток в цепи будет сначала расти до наступления резонанса, а затем убывать (рис. 1-20). Уменьшение реактивного сопротивления цепи за счет введения в цепь емкости называют последовательной компенсацией. При получается недокомпенсация, при перекомпенсация, а при полная компенсация (ток становится максимальным, а . Такой способ компенсации иногда применяют на практике для повышения в сетях. Продольная (последовательная) компенсация применена, например, в линии электропередачи Куйбышев — Москва.

Рис. 1-20

Кроме того, если взять отношение приложенного напряжения к напряжению

индуктивного (или емкостного) участка:

откуда

т. е. при напряжение на реактивном участке (и равное ему ) окажется больше приложенного в раз. Это означает, чтопри резонансе напряжений на отдельных участках Цепи могут возникнуть напряжения, опасные для изоляции обмоток приборов и машин, включенных в данную цепь. Например, при наступлении резонанса напряжений индуктивное напряжение на обмотке трансформатора (рис. 1-21) может оказаться значительно больше того напряжения, на которое рассчитана сама обмотка, в результате чего изоляция ее будет повреждена.

Однако резонанс напряжений может быть не только нежелательным явлением, которое приходится учитывать при расчетах силовых цепей, но и полезным. В частности, в радиотехнических колебательных контурахблагодаря резонансу напряжений получают значительное усиление слабых радиосигналов за счет образования больших напряжений на емкости и индуктивности. Для этого специально делают индуктивное сопротивлениеконтура во много раз больше его активного сопротивления

Рис. 1-21