Решение уравнений

ФункцияПодбор параметрапозволяет находить одно значение аргумента, соответствующее заданному значению функции (например, 0). Однако часто функция может принимать одно значение при нескольких значениях аргументов. То есть уравнение может иметь несколько корней.

Например, функция у=3*х² -15 может принимать значение 0 при двух значениях аргументов.

Однако, функция Подбор параметранайдет только один корень уравнения – самый близкий к значению в ячейке, указанной в поле Изменяя значение ячейки.

Так, если попытаться решить указанное выше уравнение с помощью Ms Excel и встроенной в него функции Подбор параметра, то исходные данные можно представить в следующем виде:

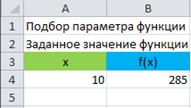
Выполнив команду Подбор параметра,необходимо заполнить поля диалогового окна следующим образом:

В результате найденным корнем уравнения будет значение 2,2360797 в ячейке А4.

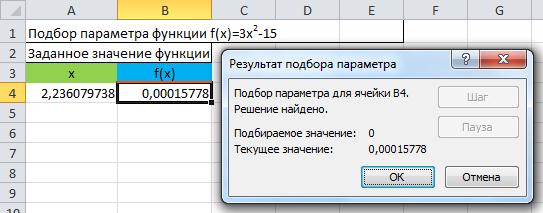
Однако, это не единственный корень. В этом можно убедиться, решив уравнение или построив график функции у=3*х²-15.

Для построения графика следует:

1) в ячейки С4-С24 ввести значения от –10 до 10 с шагом 1; в ячейку D1 – ввести формулу 3*C4*C4-15 и путём перетаскивания маркера заполнения заполнить этой формулой ячейки D5-D24;

2) выделив диапазон D4-D24, откройте вкладку Вставка, в группе Диаграммы выполните команду График с маркерами;

3) в контекстной вкладке Работа с диаграммами перейдите на вкладку Конструктор,в группеДанныевыполните командуВыбрать данные;

4) нажмите на кнопку Изменитьв областиПодписи горизонтальной оси (категории)и задайте диапазон C4-C24;

5) последовательными нажатиями кнопки ОК и ОКзакройте окно Выбор источника данных.

В результате должен быть построен график функции:

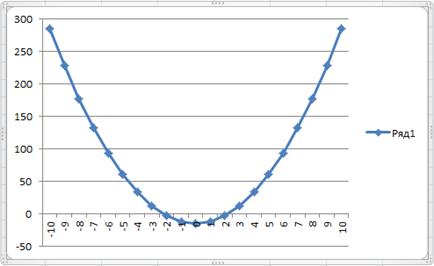
Из графика видно, что уравнение 3*x²-15=0 имеет 2 корня, к тому же эти корни примерно равны –2 и 2. Одни корень 2,2360797 нам уже известен.

Найдем второй корень. Для этого изменим значение, например, в ячейке С4 на –2 (на графике видно, что это более близкое значение к ожидаемому корню). Выделим ячейку D4 и выполним команду Подбор параметра, группы Работа с данными, вкладки Данные.Заполним поля запроса:

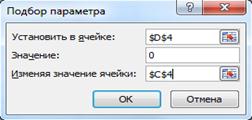
и после щелчка по кнопке ОК в ячейке С4 получим значение второго корня -2,23606503:

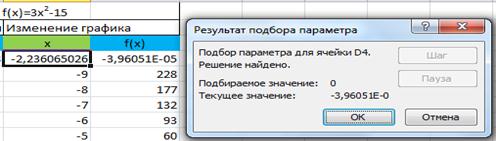
Получаемые значения корня, могут иметь несущественное отличие. Это вызвано следующим обстоятельством. По умолчанию команда Подбор параметра прекращает итерационные вычисления, когда выполняется 100 итераций, либо при получении результата, который находится в пределах 0,001 от заданного целевого значения. Если нужна большая точность, можно изменить используемые по умолчанию параметры:

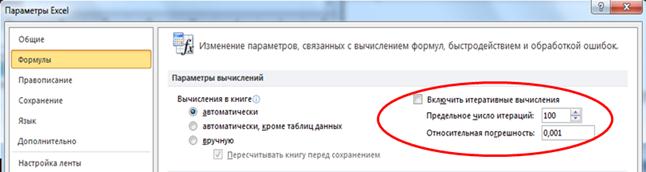
1. Во вкладке Файл выберите команду Параметры, а затем — категорию Формулы.

2. В разделе Параметры вычислений установите флажок Включить итеративные вычисления.

3. В поле Предельное число итераций введите значение больше 100, а в поле Относительная погрешность – значение меньше 0,001.

Если MS Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне запроса Результат подбора параметра и прервать вычисления, а затем нажать кнопку Шаг, чтобы просмотреть результаты каждой последовательной итерации. Когда Вы решаете задачу в пошаговом режиме, в этом окне запроса появляется кнопка Продолжить. Нажмите ее, когда решите вернуться в обычный режим подбора параметра. (Производительность современных компьютеров позволяет быстро решить задачи любой сложности, пошагово просмотреть результаты каждой последовательной итерации возможно на слабо производительных компьютерах).

Вопросы для самоконтроля

1. В каких случая может быть использована функция «Подбор параметра»?

2. Продемонстрируйте использование функции «Подбор параметра» для определения переменной a, если a+1432=8765

3. Постройте график функции y(x) = x³ + 20 на интервале x: -1000;1000 с шагом в 50. Определите значение x, где y(x) = 0. Отобразить результаты подбора графически.

4. Добавьте к диаграмме название «Подбор параметра для функции», добавьте основные и промежуточные линии на диаграмму, по оси OX установить выравнивание текста с наклоном в 90 градусов, 10 кегль шрифта.

5. Для построенного графика определите произвольные 4 точки и определите значение аргумента x и функции y(x) в этой точке.

6. Измените предельное число итераций на 1000, относительную погрешность измерений на 0,0000001.

7. Используя функцию Подбор параметра найдите корни уравнений:

7.1. ;

7.2. ;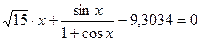

7.3. ;

7.4. ;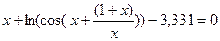

7.5. ;

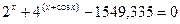7.6. ;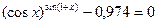

7.7. ;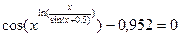

7.8. ;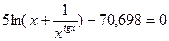

7.9. ;

7.10.