Гармонические колебания и их характеристики.

Гармоническими колебаниями называются колебания, при которых колеблющаяся физическая величина изменяется по закону синуса (или косинуса).

Различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) могут быть представлены в виде суммы (суперпозиции) гармонических колебаний.

Гармоническое колебание величины s описывается уравнением типа

где: А - амплитуда колебания - максимальное значение колеблющейся величины;

ω - круговая (циклическая) частота;

φ - начальная фаза колебания в момент времени t = 0;

(ωt+φ) - фаза колебания в момент времени t.

Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до -1, то s может принимать значения от +A до -A .

Поскольку cos(a+2π)=cosa то при гармонических колебаниях

увеличение (приращение) фазы колебания на 2π приводит к тому, что все величины, характеризующие колебание, принимают исходное значение.

Периодом колебаний Т называется наименьший промежуток времени, по истечении которого повторяются состояния колеблющейся системы (совершается одно полное колебание) и фаза колебания получает приращение 2π.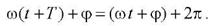

Откуда

Частотой колебаний n называется величина обратная периоду колеба­ний- число полных колебаний, совершаемых в единицу времени

Единица частоты - герц (Гц) - частота периодического процесса, при котором за 1 секунду совершается один цикл колебаний.

3.Дифференциальное уравнение гармонических колебаний.

Первая (скорость) и вторая (ускорение) производные по времени от гармонически колеблющейся величины s также совершают гармонические колебания с той же циклической частотой

Из последнего уравнения видно, что s удовлетворяет уравнению

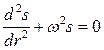или

Это уравнение называется дифференциальным уравнением гармони­ческих колебании. Его решение

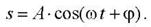
4. Метод векторных диаграмм.

Гармонические колебания изображаются графически методом вращающегося вектора амплитуды или методом векторных диаграмм.

Из произвольной точки О, выбранной на оси х, под углом φ, равным начальной фазе колебания, откладывается вектор , модуль которого равен амплитуде А, рассматриваемого

колебания. Если этот вектор будет вращаться вокруг точки О с угловой скоростью со, то проекция вектора на ось х будет совершать колебания по закону

5. Экспоненциальная форма записи гармонических колебаний.

Согласно формуле Эйлера для комплексных чисел

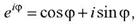
где i = - мнимая единица. Поэтому уравнение гармонического колебания можно записать в комплексной экспоненциальной форме

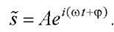
Физический смысл имеет только вещественная часть комплексной функции

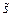, которая и представляет собой гармоническое колебание

6. Механические гармонические колебания.

Пусть материальная точка совершает прямолинейные гармонические

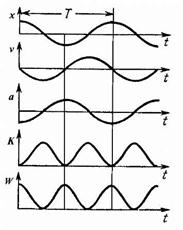
колебания вдоль оси х около положения равновесия принятого, за начало координат. Тогда для колеблющейся точки смещение.

скорость

ускорение.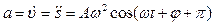

Амплитуды скорости и ускорения равны 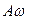и .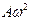

Фаза скорости отличается от фазы смещения на , а фаза ускорения на π.

Сила, действующая на колеблющуюся материальную точку массой m равна

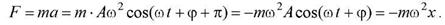
Таким образом, сила пропорциональна смещению материальной точки и направлена в сторону, противоположную смещению (к положению равновесия). Такая зависимость от смещения характерна для упругих сил и поэтому силы, которые аналогичным образом зависят от смещения, называются квазиупругими.

7. Энергия материальной точки, совершающей гармонические колебания.

Кинетическая энергия материальной точки

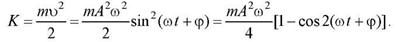
Потенциальная энергия материальной точки, совершающей гармонические колебания под действием квазиупругой силы

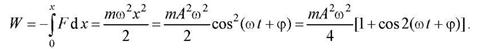
Полная энергия

остается постоянной, с течением времени происходит только превращение кинетической энергии в потенциальную и обратно.

8. Гармонический осциллятор.

Гармоническим осциллятором называется система, совершающая колебания, описываемые дифференциальным уравнением

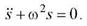
Примерами гармонического осциллятора являются пружинный, математический и физический маятники и электрический колебательный контур.

9. Пружинный маятник.

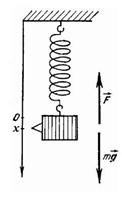Пружинный маятник - это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы

F = -kx,

где k - жесткость пружины.

Уравнение движения маятника

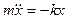или

Сравнивая это уравнение с уравнением движения

гармонического осциллятора 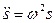, мы видим, что пружинный маятник совершает колебания по закону 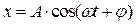с циклической частотой и периодом

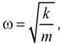
Потенциальная энергия пружинного маятника

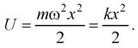
Если на маятник действует сила трения, пропорциональная скорости

, где r- коэффициент сопротивления, то колебания маятника

будут затухающими и закон движения маятника будет иметь вид или

10. Математический маятник.

Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на невесомой нерастяжимой нити длинной l, и колеблющейся под действием силы тяжести без трения.

Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити.

При малых углах отклонения 𝛼 можно считать x≈l𝛼

Возвращающая сила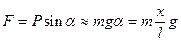

Уравнение движения

или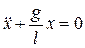

Следовательно, движение математического маятника описывается дифференциальным уравнением гармонических колебаний, то есть происходит по закону с частотой и периодом, соответственно

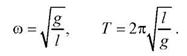
11. Физический маятник.

Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса, не проходящей через центр масс тела.

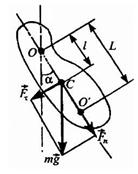Если физический маятник отклонен из положения равновесия на некоторый угол α, то момент возвращающей силы .

С другой стороны, при малых углах

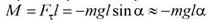
где J - момент инерции маятника относительно оси, проходящей через точку подвеса О ,

l - расстояние между точкой подвеса и центром масс С маятника,

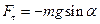- возвращающая сила (со знаком минус, поскольку она всегда направленная противоположно направлению увеличения α).

Следовательно , или .

Таким образом, при малых колебаниях физический маятник совершает гармонические колебания 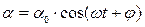с циклической частотой и периодом

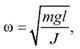
где длина 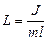- называется приведенной длиной физического маятника.

Приведенная длина физического маятника - это длина такого математического маятника, который имеет такой же период колебаний, что и данный физический маятник.

Точка О'на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качаний физического маятника.

Математический маятник можно представить как частный (предельный) случай физического маятника, вся масса которого сосредоточена в его центремасс. При этом 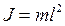, следовательно

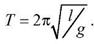
12. Электрический колебательный контур.

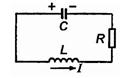Электрическим колебательным контуром называется электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R.

По закону Ома для участка цепи

или

где q и 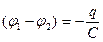- заряд конденсатора и

разность потенциалов его обкладок в произвольный момент времени t;R- электрическое сопротивление колебательного контура; 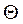- ЭДС само­индукции в катушке. Сила тока 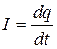, поэтому дифференциальное уравнение колебаний заряда в колебательном контуре

13. Стадии колебаний в идеализированном колебательном контуре.

Идеализированный колебательный контур - колебательный контур, у которого R = О.

Пусть в начальный момент времени t=0 конденсатор заряжен зарядом q. Тогда энергия электрического поля между обкладками конден­сатора . При замыкании конденсатора на катушку индуктивности, в контуре потечет возрастающий ток I. Энергия электрического поля начнет уменьшаться, а энергия магнитного поля катушки будет возрастать. Поскольку потерь в контуре нет (R = 0), то полная энергия сохраняется.

В момент времени (Т - период колебаний), когда конденсатор

полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения.

Стадии колебаний в контуре можно сопоставить с аналогичными стадиями механических колебаний, например, математического маятника, который в момент времени t = 0 смещен из положения равновесия и имеет максимальную потенциальную энергию . В момент времени смещение маятника равно нулю, скорость - максимальна, и потенциальная энергия полностью переходит в кинетическую энергию маятника .

Начиная с момента времени , ток в контуре будет убывать,

следовательно, магнитное поле катушки начнет ослабевать. Изменение магнитного поля вызовет индукционный ток, который, по правилу Ленца, будет иметь то же направление, что и ток разрядки конденсатора. Конденсатор начинает перезаряжаться и к моменту времени заряд на обкладках

конденсатора достигнет максимума, ток в цепи прекратится, и энергия контура снова будет равна энергии электрического поля в конденсаторе.

Для маятника это будет соответствовать максимальному смещению в направлении, противоположном первоначальному, остановке маятника в крайнем положении (υ=0) и обратному превращению кинетической энергии в

потенциальную.

Далее, все процессы в колебательном контуре будут протекать в обратном направлении и система к моменту времени t = T придет в первоначальное состояние.

Таким образом, в колебательном контуре происходят периодические изменения заряда q на обкладках конденсатора и силы тока I. Эти электрические колебания сопровождаются превращением энергий электрического и магнитного полей.

Из сравнения электрических колебаний с механическими колебаниями, следует, что:

— энергия электрического поля конденсатора аналогична потенциальной энергии маятника,

— энергия магнитного поля катушки аналогична кинетической энергии маятника,

— сила тока в контуре аналогична скорости движения маятника,

— индуктивность L выполняет функцию массы,

— сопротивление R играет роль силы трения, действующей на маятник.