
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Которые в области пространства, не содержащей свободных электрических зарядов и макроскопических токов,имеют вид




Если среда - однородный и изотропный диэлектрик, не обладающий сегнетоэлектрическими или ферромагнитными свойствами, то  и
и  , где ε0 и μ0 - электрическая и магнитная постоянные, ε и μ - диэлектрическая и магнитная проницаемости среды.
, где ε0 и μ0 - электрическая и магнитная постоянные, ε и μ - диэлектрическая и магнитная проницаемости среды.
В этом случае уравнения Максвелла

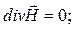


Используя  получим волновые уравнения для векторов
получим волновые уравнения для векторов  и
и  .
.
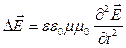

где  - оператор Лапласа,
- оператор Лапласа,  - фазовая скорость электромагнитной волны,
- фазовая скорость электромагнитной волны, 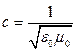 - скорость света в вакууме. Таким образом, электромагнитные поля действительно могут существовать в виде электромагнитных волн.
- скорость света в вакууме. Таким образом, электромагнитные поля действительно могут существовать в виде электромагнитных волн.
Поскольку 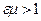 , то υ<c - скорость распространения
, то υ<c - скорость распространения
электромагнитных волн в веществе всегда меньше, чем в вакууме.
48. Поперечность электромагнитных волн.
Следствия теории Максвелла:
 (1) Векторы
(1) Векторы  и
и 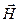 напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору
напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору  скорости распространения волны, причем векторы
скорости распространения волны, причем векторы 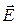 ,
, 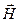 и
и  образуют правовинтовую систему. (Только EY≠0 и HZ≠0).
образуют правовинтовую систему. (Только EY≠0 и HZ≠0).
(2)В электромагнитной волне векторы  и
и  всегда колеблются водинаковых фазах, причем мгновенные значения E и H любой точке связаны соотношением
всегда колеблются водинаковых фазах, причем мгновенные значения E и H любой точке связаны соотношением  .
.
Волновым уравнениям

удовлетворяют плоские монохроматические электромагнитные волны, описываемые уравнениями  ,
, 
где Е0 и Н0 - амплитуды напряженностей электрического и магнитного полей
волны, ω - круговая частота волны,  - волновое число, φ - начальная
- волновое число, φ - начальная
фаза колебаний (одинаковая, поскольку колебания  и
и  происходят с одинаковой фазой).
происходят с одинаковой фазой).
49. Отражение и преломление электромагнитных волн на границе раздела двух диэлектрических сред.
Пусть на границу раздела двух диэлектриков падает плоская электромагнитная волна. В таком случае, как показывает опыт, от границы раздела диэлектриков будут распространяться две плоские волны - отраженная и преломленная.
Запишем выражения для падающей (/), отраженной (г) и преломленной (d) волн в комплексной экспоненциальной форме

Здесь 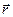 - радиус-вектор, ω и υ - частота и скорости волн,
- радиус-вектор, ω и υ - частота и скорости волн,  - амплитуды волн,
- амплитуды волн,  - единичные векторы, показывающие направление распространения соответствующих волн. Условие
- единичные векторы, показывающие направление распространения соответствующих волн. Условие  определяет
определяет
плоскость, перпендикулярную к  , поэтому данная система выражений описывает плоские волны, распространяющиеся вдоль векторов
, поэтому данная система выражений описывает плоские волны, распространяющиеся вдоль векторов 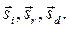
Граничные условия для тангенциальных (𝜏) компонент векторов напряженности электрического и магнитного поля в любой точке границы раздела сред (1) и (2) имеют вид (см. 4-п.45)  ,
,  .
.
Для нашего случая, граничные условия для электрического вектора
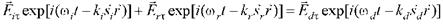
Для выполнения этого равенства в любой момент времени t в любой точке границы раздела необходимо и достаточно, чтобы во всех трех показателях экспонент были одинаковы коэффициенты при t и при проекции  радиус-вектора
радиус-вектора 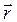 на границу раздела, т.е. чтобы выполнялись равенства
на границу раздела, т.е. чтобы выполнялись равенства

Следовательно, частоты всех трех волн должны быть равны между собой, поскольку частоты колебаний зарядов в диэлектрической среде, вынуждаемых колебаниями электрического вектора, совпадают с частотой вынуждающей силы. Кроме того, единичные векторы  находятся в одной плоскости, проходящей через нормаль к плоскости раздела (плоскость падения).
находятся в одной плоскости, проходящей через нормаль к плоскости раздела (плоскость падения).
 Выберем систему координат таким образом, чтобы плоскость хОу совпадала с плоскостью раздела сред, а плоскость zOx - с плоскостью падения, причем ось Oz направим из среды I в среду II (см. рисунок). Обозначим φ - угол между
Выберем систему координат таким образом, чтобы плоскость хОу совпадала с плоскостью раздела сред, а плоскость zOx - с плоскостью падения, причем ось Oz направим из среды I в среду II (см. рисунок). Обозначим φ - угол между  и осью Oz (угол падения),
и осью Oz (угол падения),  - угол между
- угол между  и Oz (
и Oz (  - угол отражения), ψ- угол между
- угол отражения), ψ- угол между  и Oz (угол преломления). В этой системе координат у-компоненты векторов
и Oz (угол преломления). В этой системе координат у-компоненты векторов  равны нулю, а х - компоненты можно выразить следующим образом
равны нулю, а х - компоненты можно выразить следующим образом
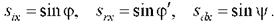
Следовательно, равенство  примет вид
примет вид

Первое равенство означает, что  - закон отражения в оптике.
- закон отражения в оптике.
Из второго равенства следует оптический закон преломления.
Показателем преломления среды п называется величина, равная отношению скорости с электромагнитных волн в вакууме к их фазовой скорости  в среде
в среде

Для среды, не обладающей ферромагнитными свойствами ,  и
и
практически можно считать, что

В этом случае для преломленной волны имеем закон преломления

Разложим амплитуды электрического и магнитного векторов на компоненты  ,
,  ,
,  ,
,  , лежащие соответственно в плоскости падения и перпендикулярные к ней. Взаимные ориентации векторов
, лежащие соответственно в плоскости падения и перпендикулярные к ней. Взаимные ориентации векторов  ,
,  ,
,  ,
,  приведены на рисунках (а) и (б).
приведены на рисунках (а) и (б).
Для компонент напряженности электрического вектора, лежащих в плоскости падения (рис. (а)), граничные условия (с учетом  ,
,  и
и  ) имеют вид
) имеют вид
 и
и 
Решая эту систему уравнений и используя закон преломления, найдем выражения для амплитудных коэффициентов отражения r|| и пропускания t|| для волны, линейно-поляризованной в плоскости падения
 (*)
(*)
Для компонент напряженностей электрического вектора, перпендикулярных к плоскости падения (рис. (б)), граничные условия принимают вид
 и
и 
Амплитудные коэффициенты отражения и пропускания  и
и  .
. 
Соотношения (*) и (**) между амплитудами падающей, отраженной и преломленной волн называются формулами Френеля.
В формулах Френеля  и
и 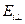 - величины положительные, а
- величины положительные, а  и
и  при любых возможных углах падения и преломления также положительны, что свидетельствует о совпадении фаз преломленной и падающей волн. Величины
при любых возможных углах падения и преломления также положительны, что свидетельствует о совпадении фаз преломленной и падающей волн. Величины  и
и  могут быть как отрицательными, так и положительными. В первом случае фаза колебаний вектора
могут быть как отрицательными, так и положительными. В первом случае фаза колебаний вектора  изменяется при отражении на π (фаза колебаний вектора
изменяется при отражении на π (фаза колебаний вектора  при этом сохраняется). Во втором случае (см. рис.) отражение происходит без изменения фазы колебаний вектора
при этом сохраняется). Во втором случае (см. рис.) отражение происходит без изменения фазы колебаний вектора  (соответственно фаза колебаний вектора
(соответственно фаза колебаний вектора  при отражении изменяется на π). Значения сдвига фаз колебаний вектора
при отражении изменяется на π). Значения сдвига фаз колебаний вектора  при отражении электромагнитных волн в зависимости от угла падения и значений показателей преломления приведены в таблице.
при отражении электромагнитных волн в зависимости от угла падения и значений показателей преломления приведены в таблице. 
Таким образом, при малых углах падения (φ+ψ<π/2) фаза обеих компонент электрического вектора отраженной волны противоположна фазе падающей для случая, когда п2 > п1, и совпадает с фазой падающей волны при n2 < n1.
В частности это имеет место и при нормальном падении.
Явление изменения фазы волны на π при отражении от среды с большим показателем преломления - "потеря полуволны" - играет значительную роль в интерференционных и дифракционных явлениях, которые рассматриваются в курсе "Оптика".
Рассмотрим теперь случай, когда выполняется условие φ+ψ=π/2 (и, следовательно, tg(φ+ψ)→∞). Угол падения φБ, при котором отраженный и
преломленный лучи взаимно перпендикулярны, называется углом Брюстера.
Из закона преломления следует, что 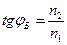 .
.
При этом  и в отраженной волне присутствует только
и в отраженной волне присутствует только  компонента (отраженная волна линейно поляризована в плоскости, перпендикулярной плоскости падения).
компонента (отраженная волна линейно поляризована в плоскости, перпендикулярной плоскости падения).
50. Энергия электромагнитных волн.
Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей we и wm электрического и магнитного полей

Так как  , то
, то  .
.
Плотность потока энергии  .
.
Вектор 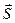 плотности потока энергии электромагнитной волны называется вектором Умова-Пойтинга.
плотности потока энергии электромагнитной волны называется вектором Умова-Пойтинга.

Вектор 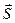 направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны. Скалярная величина I, равная модулю среднего значения
направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны. Скалярная величина I, равная модулю среднего значения
вектора Умова-Пойтинга, называется интенсивностью волны  .
.
Интенсивность волны численно равна энергии, переносимой волной за единицу времени сквозь единицу площади поверхности, нормальной к направлению распространения волны. Интенсивность синусоидальной волны пропорциональна квадрату ее амплитуды.
51. Излучение электрического диполя.
Процесс возбуждения электромагнитных волн какой-либо системой в окружающем пространстве называется излучением этих волн, а сама система называется излучающей системой. Поле электромагнитных волн называется полем излучения.
Простейшим излучателем электромагнитных волн является электрический диполь (см. 3-п.13), электрический момент которого изменяется по гармоническому закону

Примером подобного диполя может служить система, состоящая из покоящегося положительного заряда +q и отрицательного заряда -q,
гармонически колеблющегося вдоль направления  с частотой
с частотой 
Как показывает теория, в точках пространства, отстоящих от диполя на расстояниях г, значительно превышающих длину излучаемой волны  (эта область пространства называется волновой зоной диполя), интенсивность излучения диполя
(эта область пространства называется волновой зоной диполя), интенсивность излучения диполя


Где θ - угол между осью диполя и направлением излучения. Зависимость I(θ) при фиксированном г называют полярной диаграммой направленности излучения диполя (индикат- риссой излучения). Из этой диаграммы видно, что диполь сильнее всего излучает в направлениях, перпендикулярных его оси (θ=π/2). Вдоль своей оси (θ=0 и θ=π) диполь не излучает вообще. Диаграмма направленности позволяет формировать излучение с определенными пространственными характеристиками и используется при конструировании антенн.
52. Шкала электромагнитных волн.

Электромагнитные волны, обладая широким диапазоном частот (или длин волн), отличаются по способам их генерации и регистрации, а также по своим свойствам. Поэтому электромагнитные волны условно делятся на несколько видов: радиоволны (λ>50мкм), световые волны (инфракрасные волны (770нм<λ<1мм) видимый свет (380нм<λ<770нм), ультрафиолетовое излучение (10нм<λ<380нм)); рентгеновское излучение (0,01нм<λ<100нм) и γ-излучение (λ<0,1 нм).
ОПТИКА
Геометрическая оптика
Оптика - раздел физики, который изучает природу света, световые явления и взаимодействие света с веществом.
Оптическое излучение представляет собой электромагнитные волны, и поэтому оптика является частью общего учения об электромагнитном поле.
В зависимости от круга рассматриваемых явлений оптику делят на геометрическую (лучевую), волновую (физическую), квантовую (корпускулярную).
1. Основные законы геометрической оптики.
Еще до установления природы света были известны следующие законы: Закон прямолинейного распространения света - свет в оптически однородной среде распространяется прямолинейно.
 Световой луч - линия, вдоль которой переносится световая энергия. В однородной среде лучи света представляют собой прямые линии.
Световой луч - линия, вдоль которой переносится световая энергия. В однородной среде лучи света представляют собой прямые линии.
Закон независимости световых пучков - эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены.
Закон отражения - отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения; угол отражения i/ равен углу падения i.

Закон преломления - луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела двух сред в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред, равная - относительному показателю преломления второй среды относительно первой, который равен отношению абсолютных показателей преломления двух сред.


Следовательно, закон преломления будет иметь вид


Абсолютным показателем преломления среды называется величина n, равная отношению скорости электромагнитных волн в вакууме с к их фазовой скорости υ в среде.
где ε и µ- соответственно электрическая и магнитная проницаемость среды.
2. Полное отражение.
Если свет распространяется из среды с большим показателем преломления n1 (оптически более плотной) в среду с меньшим показателем преломления n2 (оптически менее плотную) (n1 >n2) (например, из стекла в воздух или из воды в воздух), то

Следовательно, угол преломления i2 больше угла падения . Увеличивая угол падения, при некотором предельном угле iпр угол преломления окажется равным π/2. При углах падения i1 > iпр весь падающий свет полностью отражается.
 При углах падения
При углах падения  луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы.
луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы.
Это явление называется полным внутренним отражением света.
Предельный угол определяется соотношением

Явление полного отражения используется в призмах полного отражения и световодах.
3. Линзы.
 Линзой называется прозрачное тело, ограниченное с двух сторон криволинейной поверхностью. (В частном случае одна из поверхностей может быть плоской). По внешней форме линзы делятся на
Линзой называется прозрачное тело, ограниченное с двух сторон криволинейной поверхностью. (В частном случае одна из поверхностей может быть плоской). По внешней форме линзы делятся на
1) двояковыпуклые;
2) плосковыпуклые;
3) двояковогнутые;
4) плосковогнутые;
5) выпукло-вогнутые.
Линза называется тонкой, если ее толщина значительно меньше, чем радиусы кривизны R1 и R2 обеих поверхностей. На оптических схемах линзы обычно обозначают двунаправленной стрелкой.
Радиус кривизны R > О для выпуклой поверхности;
 R < О для вогнутой.
R < О для вогнутой.
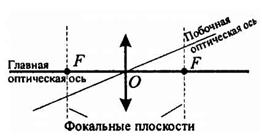
Прямая проходящая через центры кривизны поверхностей линзы называется главной оптической осью.
Оптическим центром линзы (обычно обозначается О) называется точка, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь. Побочными оптическими осями называются прямые, проходящие через оптический центр линзы и не совпадающие с главной оптической осью.
Фокусом линзы F называется точка, лежащая на главной оптической оси, в которой пересекаются лучи параксиального (приосевого) светового пучка, распространяющиеся параллельно главной оптической оси.
Фокальной плоскостью называется плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.
 Фокусным расстоянием / называется расстояние между оптическим центром линзы О и ее фокусом F:
Фокусным расстоянием / называется расстояние между оптическим центром линзы О и ее фокусом F:

Формула тонкой линзы:

где а и b - расстояния от линзы до предмета и его изображения. Если а равно бесконечности, т.е. лучи падают на линзу параллельным пучком (а), то b = f. Если  , т.е. изображение находится в бесконечности (б), и, следовательно, лучи выходят из линзы параллельным пучком, то а = f .
, т.е. изображение находится в бесконечности (б), и, следовательно, лучи выходят из линзы параллельным пучком, то а = f .
Фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны.
Величина Ф = 1/f называется оптической силой линзы. Ее единица - диоптрия (дптр) - оптическая сила линзы с фокусным расстоянием 1м.
Линзы с положительной оптической силой являются собирающими, с отрицательной - рассеивающими.
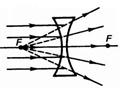 В отличие от собирающей линзы, рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси.
В отличие от собирающей линзы, рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси.
4. Аберрации оптических систем.
В реальных оптических системах используются пучки отличающиеся от параксиальных, показатель преломления линз зависит от длины волны падающего света, а сам свет немонохроматичен. Искажения оптического изображения которые возникают при этом называются аберрациями.
 Сферическая аберрация. Фокус S" для лучей, более удаленных от оптической оси чем параксиальные, находится ближе, чем фокус S' параксиальных лучей. В результате изображение светящейся точки имеет вид расплывчатого пятна.
Сферическая аберрация. Фокус S" для лучей, более удаленных от оптической оси чем параксиальные, находится ближе, чем фокус S' параксиальных лучей. В результате изображение светящейся точки имеет вид расплывчатого пятна.
 Сферическая аберрация является частным случаем астигматизма.
Сферическая аберрация является частным случаем астигматизма.
Кома. Если через оптическую систему проходит широкий пучок от точечного источника света, расположенного не на оптической оси, то получаемое изображение этой точки будет в виде освещенного пятна неправильной формы.
Точечным источником света называется источник, размерами которого можно пренебречь.
 Астигматизм. Погрешность, обусловленная неодинаковостью кривизны оптической поверхности в разных плоскостях сечения падающего на нее светового пучка.
Астигматизм. Погрешность, обусловленная неодинаковостью кривизны оптической поверхности в разных плоскостях сечения падающего на нее светового пучка.
Дисторсия. Погрешность, при которой при больших углах падения лучей на линзу линейное увеличение для точек предмета, которые находятся на разных расстояниях от главной
 оптической оси, несколько различается. В результате нарушается геометрическое подобие между предметом (например, прямоугольная сетка) и его изображением (рисунок (b) - подушкообразная дисторсия, (с) - бочкообразная дисторсия).
оптической оси, несколько различается. В результате нарушается геометрическое подобие между предметом (например, прямоугольная сетка) и его изображением (рисунок (b) - подушкообразная дисторсия, (с) - бочкообразная дисторсия).
Хроматическая аберрация. При падении на оптическую систему белого
 света отдельные составляющие его монохроматические лучи фокусируются в разных точках (наибольшее фокусное расстояние имеют красные лучи, наименьшее - фиолетовые), поэтому изображение размыто и по краям окрашено.
света отдельные составляющие его монохроматические лучи фокусируются в разных точках (наибольшее фокусное расстояние имеют красные лучи, наименьшее - фиолетовые), поэтому изображение размыто и по краям окрашено.
5. Энергетические величины в фотометрии.
Фотометрия - раздел оптики, в котором рассматриваются энергетические характеристики оптического излучения в процессах его испускания, распространения и взаимодействия с веществом. При этом значительное внимание уделяется вопросам измерения интенсивности света и его источников.
Энергетические величины в фотометрии - характеризуют энергетические параметры оптического излучения без учета особенностей его воздействия на тот или иной приемник излучения.
Поток излучения Фе - величина, равная отношению энергии W излучения ко времени t, за которое излучение произошло (мощность излучения). Единица потока излучения - ватт (Вт). 
Энергетическая светимость (излучательность) Re - величина, равная отношению потока излучения Фе, испускаемого поверхностью, к площади S сечения, сквозь которое этот поток проходит (поверхностная плотность потока излучения). Единица энергетической светимости - ватт на метр в квадрате (Вт/м2). 
Энергетическая сила света (сила излучения) Iе - величина, равная отношению потока излучения  точечного источника к телесному углу ω в пределах которого это излучение распространяется. Единица энергетической силы света - ватт на стерадиан (Вт/ср).
точечного источника к телесному углу ω в пределах которого это излучение распространяется. Единица энергетической силы света - ватт на стерадиан (Вт/ср). 
Энергетическая яркость (лучистость) Ве - величина, равная отношению энергетической силы света 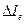 элемента излучающей поверхности к площади
элемента излучающей поверхности к площади  проекции этого элемента на плоскость, перпендикулярную направлению наблюдения. Единица энергетической яркости - ватт на стерадиан-метр в квадрате (Вт/(срм2)).
проекции этого элемента на плоскость, перпендикулярную направлению наблюдения. Единица энергетической яркости - ватт на стерадиан-метр в квадрате (Вт/(срм2)). 
Энергетическая освещенность (облученность) Ее - характеризует величину потока излучения, падающего на единицу освещаемой поверхности. Единица энергетической освещенности - ватт на метр в квадрате (Вт/м2).
Дата добавления: 2014-10-31; просмотров: 560; Мы поможем в написании вашей работы!; Нарушение авторских прав |