
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
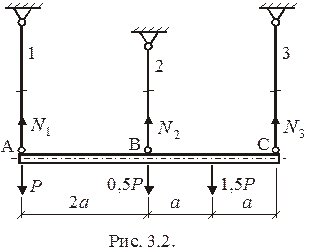 Рассматривается один раз статически неопределимая система - балка, подвешенная на трех стержнях (рис. 3.2). Жесткость на изгиб балки считается бесконечной (
Рассматривается один раз статически неопределимая система - балка, подвешенная на трех стержнях (рис. 3.2). Жесткость на изгиб балки считается бесконечной (  ). Длины стержней выражены через общую длину
). Длины стержней выражены через общую длину  :
:  . Площади поперечных сечений стержней выражаются через заданную общую площадь
. Площади поперечных сечений стержней выражаются через заданную общую площадь 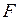 :
: 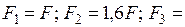
 . Балка нагружена тремя силами, выраженными через общую силу
. Балка нагружена тремя силами, выраженными через общую силу 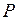 . От этих сил в стержнях 1, 2, 3 возникают соответственно продольные силы
. От этих сил в стержнях 1, 2, 3 возникают соответственно продольные силы  . Диаграмма
. Диаграмма  материала берется согласно рис. 3.1. Требуется определить предельную нагрузку (силу)
материала берется согласно рис. 3.1. Требуется определить предельную нагрузку (силу)  .
.
Из рисунка 3.2 видно, что предельное состояние (разрушение) системы наступает при условии  в каких-либо двух стержнях. С целью определения номеров этих стержней сначала определим силы
в каких-либо двух стержнях. С целью определения номеров этих стержней сначала определим силы  в стержнях при условии, что материал всех стержней работает в упругой области диаграммы
в стержнях при условии, что материал всех стержней работает в упругой области диаграммы  . Для определения этих сил можно составить два уравнения равновесия и уравнение совместности перемещений точек
. Для определения этих сил можно составить два уравнения равновесия и уравнение совместности перемещений точек  и
и  (рис. 3.3):
(рис. 3.3):

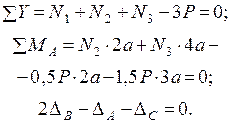
Перемещения  (удлинения стержней 1, 2, 3) по закону Гука пропорциональны силам
(удлинения стержней 1, 2, 3) по закону Гука пропорциональны силам  :
:
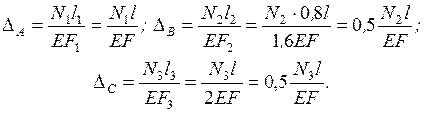
С учетом данного условия получаем систему линейных алгебраических уравнений
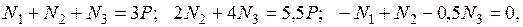
из которой определяются силы  :
: 
 . Это дает напряжения в стержнях:
. Это дает напряжения в стержнях:

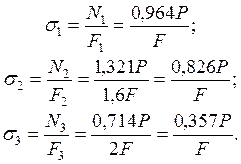
Полученные результаты показывают, что при возрастании нагрузки предельное состояние 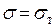 сначала реализуется в стержне 1, затем в стержне 2, после чего согласно принятой диаграмме
сначала реализуется в стержне 1, затем в стержне 2, после чего согласно принятой диаграмме  (рис. 3.1) наступает потеря несущей способности (разрушение) системы. Предельная нагрузка определяется из суммы моментов сил относительно точки С (рис. 3.4):
(рис. 3.1) наступает потеря несущей способности (разрушение) системы. Предельная нагрузка определяется из суммы моментов сил относительно точки С (рис. 3.4):

Подставляя в это уравнение 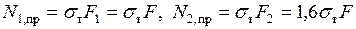 и решая его, получаем
и решая его, получаем 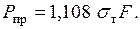
Дата добавления: 2014-11-13; просмотров: 338; Мы поможем в написании вашей работы!; Нарушение авторских прав |