
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
СИСТЕМ МЕТОДОМ СИЛ
СТЕПЕНЬ СТАТИЧЕСКОЙ НЕОПРЕДЕЛИМОСТИ
ПЛОСКОЙ СТЕРЖНЕВОЙ СИСТЕМЫ
Статически неопределимыми называются системы, которые имеют лишние (с точки зрения обеспечения геометрической неизменяемости) связи. Степень статической неопределимости (ССН) связана с числом степеней свободы системы простым соотношением:  . Для плоских рам, имеющих замкнутые бесшарнирные контуры, ССН увеличивается на 3К, где К - число таких контуров:
. Для плоских рам, имеющих замкнутые бесшарнирные контуры, ССН увеличивается на 3К, где К - число таких контуров:  . На рис. 2.1 приведены примеры определения ССН некоторых плоских стержневых систем.
. На рис. 2.1 приведены примеры определения ССН некоторых плоских стержневых систем.


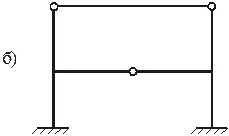


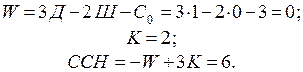
Рис. 2.1.
ОСНОВНАЯ СИСТЕМА МЕТОДА СИЛ
В методе сил любая статически неопределимая система рассчитывается с помощью соответствующей статически определимой системы, полученной из заданной системы путем отбрасывания лишних связей и замены их неизвестными силами (реакциями)  . Полученная таким образом статически определимая система называется основной системой (ОС) метода сил. Из заданной статически неопределимой системы можно получить несколько вариантов ОС, отбрасывая различным образом лишние связи (рис. 2.2). Наиболее рациональной из всех возможных ОС является такая, в которой реакции опор и внутренние обобщенные силы определяются как можно проще (рис. 2б, 2в).
. Полученная таким образом статически определимая система называется основной системой (ОС) метода сил. Из заданной статически неопределимой системы можно получить несколько вариантов ОС, отбрасывая различным образом лишние связи (рис. 2.2). Наиболее рациональной из всех возможных ОС является такая, в которой реакции опор и внутренние обобщенные силы определяются как можно проще (рис. 2б, 2в).
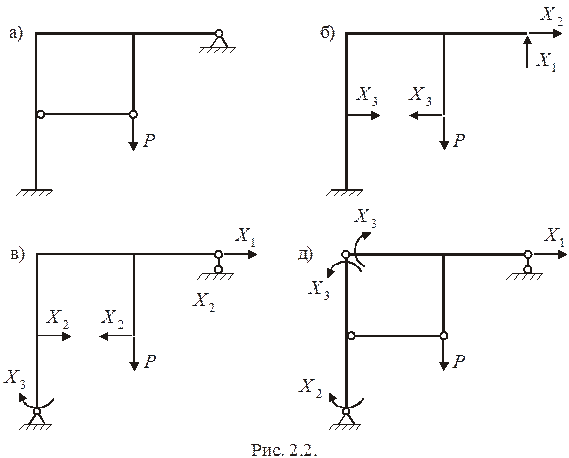
КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ
Неизвестные силы  определяются из условия отсутствия перемещений (абсолютных или относительных) в ОС в направлениях этих сил. Эти условия записываются в виде канонических уравнений метода сил. Рассмотрим получение данных уравнений на примере системы, имеющей
определяются из условия отсутствия перемещений (абсолютных или относительных) в ОС в направлениях этих сил. Эти условия записываются в виде канонических уравнений метода сил. Рассмотрим получение данных уравнений на примере системы, имеющей  (рис. 2.3а). Будем считать, что перемещения в системе возрастают прямо пропорционально заданной нагрузке. Такие системы принято называть линейно-деформируемыми. Тогда исходное состояние ОС (рис. 2.3б) можно разложить на три независимых состояния: состояние от силы
(рис. 2.3а). Будем считать, что перемещения в системе возрастают прямо пропорционально заданной нагрузке. Такие системы принято называть линейно-деформируемыми. Тогда исходное состояние ОС (рис. 2.3б) можно разложить на три независимых состояния: состояние от силы  (рис. 2.3в); состояние от силы
(рис. 2.3в); состояние от силы  (рис. 2.3г) и состояние от заданной нагрузки (рис. 2.3д). От силы
(рис. 2.3г) и состояние от заданной нагрузки (рис. 2.3д). От силы  в направлениях
в направлениях  и
и  в ОС возникают соответственно перемещения
в ОС возникают соответственно перемещения  и
и  . От силы
. От силы  в этих же направлениях получаются соответственно перемещения
в этих же направлениях получаются соответственно перемещения  и
и  . От нагрузки в направлениях сил
. От нагрузки в направлениях сил  и
и  в ОС возникают соответственно перемещения
в ОС возникают соответственно перемещения  и
и  .
.
Алгебраическая сумма отмеченных перемещений в ОС в направлении каждой из неизвестных сил  и
и  должна быть равна нулю:
должна быть равна нулю:

 Перемещения в ОС от сил
Перемещения в ОС от сил  и
и  пропорциональны этим силам:
пропорциональны этим силам:
 Каждый коэффициент
Каждый коэффициент 
 по физическому смыслу представляет перемещение в ОС в направлении силы
по физическому смыслу представляет перемещение в ОС в направлении силы  от силы
от силы  и называется коэффициентом податливости. Подставляя данные выражения в предыдущие равенства, получаем канонические уравнения метода сил для системы, имеющей
и называется коэффициентом податливости. Подставляя данные выражения в предыдущие равенства, получаем канонические уравнения метода сил для системы, имеющей  :
:
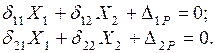
При  получаем соответственно
получаем соответственно  таких уравнений, содержащих
таких уравнений, содержащих  неизвестных сил:
неизвестных сил:
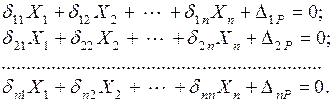
Данные уравнения можно представить в матричной форме:
 .
.
Здесь
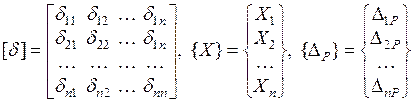
представляют соответственно матрицу податливости, вектор неизвестных сил и вектор свободных членов канонических уравнений.
Свойства матрицы податливости. Матрица  всегда является симметричной (
всегда является симметричной ( 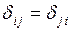 ) и положительно определенной (
) и положительно определенной (  ).
).
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ПРИ НЕИЗВЕСТНЫХ
И СВОБОДНЫХ ЧЛЕНОВ КАНОНИЧЕСКИХ УРАВНЕНИЙ
Коэффициенты при неизвестных (коэффициенты податливости)  и свободные члены
и свободные члены  канонических уравнений по физическому смыслу представляют перемещения в ОС в направлениях неизвестных сил
канонических уравнений по физическому смыслу представляют перемещения в ОС в направлениях неизвестных сил  . Поэтому их можно определить по формуле Мора. Для систем, в которых перемещения обусловлены в основном деформациями изгиба (балки, рамы, арки)
. Поэтому их можно определить по формуле Мора. Для систем, в которых перемещения обусловлены в основном деформациями изгиба (балки, рамы, арки)
 .
.
Здесь  - изгибающие моменты в ОС соответственно от сил
- изгибающие моменты в ОС соответственно от сил  ,
,  и заданной нагрузки, изображаемые в виде соответствующих эпюр. При расчете методом сил статически неопределимых ферм
и заданной нагрузки, изображаемые в виде соответствующих эпюр. При расчете методом сил статически неопределимых ферм  и
и  определяются по формулам
определяются по формулам
 ,
,
где  - продольные силы в стержнях ОС соответственно от сил
- продольные силы в стержнях ОС соответственно от сил  ,
,  и заданной нагрузки (
и заданной нагрузки (  - номер стержня);
- номер стержня);  - продольные жесткости и длины стержней ОС.
- продольные жесткости и длины стержней ОС. 
ОПРЕДЕЛЕНИЕ ОБОБЩЕННЫХ ВНУТРЕННИХ СИЛ
В ЗАДАННОЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ СИСТЕМЕ
После определения сил  из канонических уравнений ОС становится эквивалентной заданной статически неопределимой системе. Поэтому для определения обобщенных внутренних сил
из канонических уравнений ОС становится эквивалентной заданной статически неопределимой системе. Поэтому для определения обобщенных внутренних сил  (построения эпюр
(построения эпюр 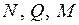 ) в заданной системе можно по-прежнему воспользоваться ОС при совместном действии заданной нагрузки и найденных сил
) в заданной системе можно по-прежнему воспользоваться ОС при совместном действии заданной нагрузки и найденных сил  . Методика определения
. Методика определения 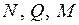 в ОС такая же, как в любой статически определимой системе.
в ОС такая же, как в любой статически определимой системе.
Верность расчета контролируется проверкой равновесия внешних и внутренних обобщенных сил в узлах конструкции, а также с помощью кинематической проверки. Смысл последней состоит в проверке отсутствия перемещений в заданной системе в направлениях сил  , действовавших в ОС:
, действовавших в ОС:
 .
.
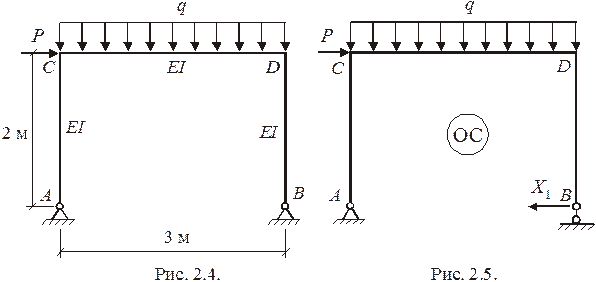
Пример расчета статически неопределимой рамы (рис. 2.4) методом сил.
Дано: 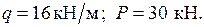
Построить эпюры 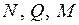 .
.
1. Определение ССН и выбор ОС
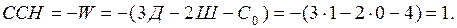
Выбираем ОС, отбрасывая одну лишнюю связь и заменяя ее неизвестной силой  (рис. 2.5), определяемой из канонического уравнения
(рис. 2.5), определяемой из канонического уравнения
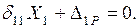
2. Построение эпюр  ,
,  в ОС
в ОС
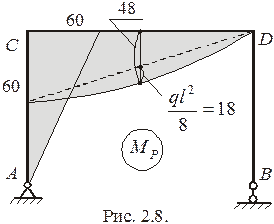
Эпюры  и
и  (рис. 2.6, рис. 2.8) строятся в ОС соответственно от силы
(рис. 2.6, рис. 2.8) строятся в ОС соответственно от силы  и нагрузки. Для построения данных эпюр в выбранной ОС достаточно определить в обоих состояниях только реакцию
и нагрузки. Для построения данных эпюр в выбранной ОС достаточно определить в обоих состояниях только реакцию  (рис. 2.6, рис. 2.7).
(рис. 2.6, рис. 2.7).
3. Определение  и силы
и силы 
Значения  определяются по формуле Мора. Интегралы Мора на каждом участке находятся по справочным формулам перемножения эпюр или по правилу Верещагина.
определяются по формуле Мора. Интегралы Мора на каждом участке находятся по справочным формулам перемножения эпюр или по правилу Верещагина.
 ;
;
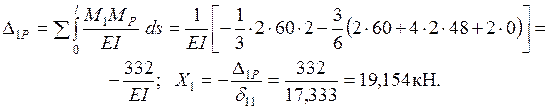

4. Построение эпюр 
Эпюры  в заданной статически неопределимой системе строятся с помощью ОС. Для этого сначала определяются реакции опор, возникающие в ОС при совместном действии нагрузки и силы
в заданной статически неопределимой системе строятся с помощью ОС. Для этого сначала определяются реакции опор, возникающие в ОС при совместном действии нагрузки и силы  (рис. 2.9а):
(рис. 2.9а):
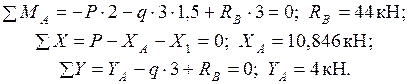
Далее определяются значения 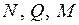 на участках рамы.
на участках рамы.
Участок АС: 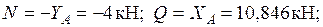

Участок CD: 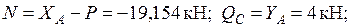
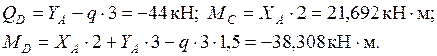
Участок BD: 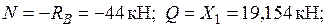
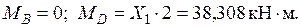
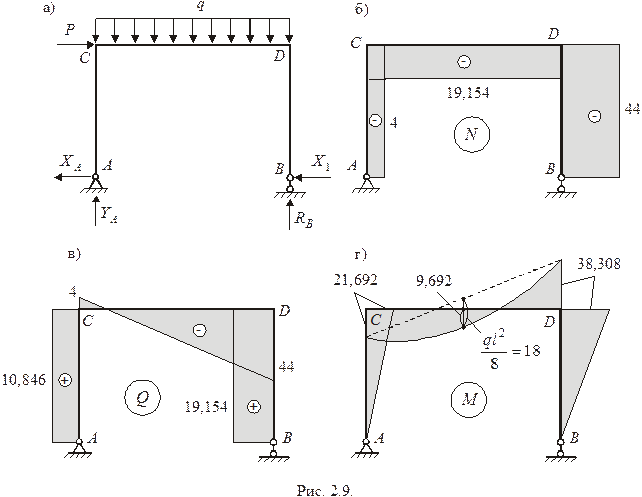
По полученным результатам строятся эпюры 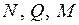 (рис. 2.9б, 2.9в, 2.9г).
(рис. 2.9б, 2.9в, 2.9г).
5. Проверка равновесия узлов
Равновесие изгибающих моментов в узлах C и D рамы следует непосредственно из эпюры M (рис. 2.9г). Поэтому достаточно проверить лишь равновесие горизонтальных и вертикальных сил в данных узлах (рис. 2.10). Направления 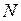 и
и 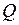 при этом берутся действительными.
при этом берутся действительными.
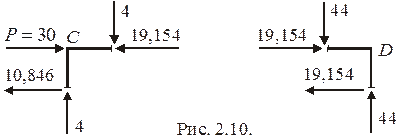
Для узла С: Для узла D:


Узлы C и D находятся в равновесии.
6. Кинематическая проверка

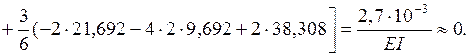
Дата добавления: 2014-11-13; просмотров: 1174; Мы поможем в написании вашей работы!; Нарушение авторских прав |