
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМАХ
ОБЩИЕ ПРИНЦИПЫ ОПРЕДЕЛЕНИЯ ОБОБЩЕННЫХ
ВНУТРЕННИХ СИЛ В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ
СТЕРЖНЕВЫХ СИСТЕМАХ
Для определения обобщенных внутренних сил  во всех статически определимых системах можно применить способ сечений. Суть данного способа состоит в следующем:
во всех статически определимых системах можно применить способ сечений. Суть данного способа состоит в следующем:
а) в интересующем месте конструкции проводится сквозное сечение, перпендикулярное осям стержней;
б) составляются уравнения равновесия для части конструкции, расположенной с какой-либо стороны от проведенного сечения с учетом обобщенных внутренних сил  в этом сечении (последние необходимо прикладывать в положительных направлениях согласно правилам, изложенным в параграфе 0.2).
в этом сечении (последние необходимо прикладывать в положительных направлениях согласно правилам, изложенным в параграфе 0.2).
в) из уравнений равновесия определяются обобщенные внутренние силы  в сечении.
в сечении.
Пример: Определить обобщенные внутренние силы  в сечении “k” плоской статически определимой рамы (рис. 1.1).
в сечении “k” плоской статически определимой рамы (рис. 1.1).

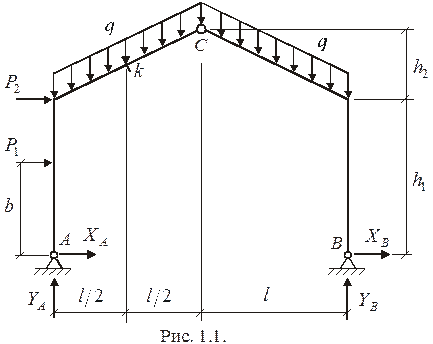
Для определения обобщенных внутренних сил  в сечении “k” достаточно найти реакции только левой опоры, составляя для этого два уравнения равновесия:
в сечении “k” достаточно найти реакции только левой опоры, составляя для этого два уравнения равновесия:
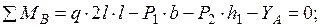
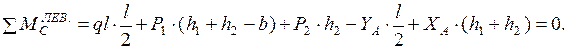
 Из этих уравнений получаем
Из этих уравнений получаем
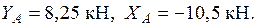
Составляем три уравнения равновесия для части рамы, расположенной слева от сечения “k” (рис. 1.2):
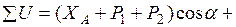
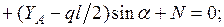
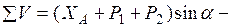
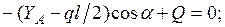
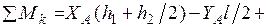
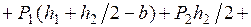
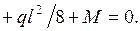
Значения  определяются через
определяются через  :
: 
 Из этих уравнений получаем выражения для определения
Из этих уравнений получаем выражения для определения  в сечении “k”:
в сечении “k”:
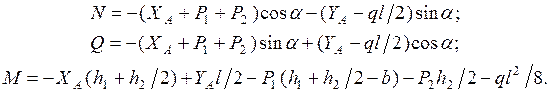
Вычисления дают:  .
.
Анализ полученных выше выражений позволяет сформулировать правила знаков для прямого получения  от действия внешних сил (без составления уравнений равновесия отсеченной части конструкции): а) если сила растягивает стержень в заданном сечении, то она дает в нем
от действия внешних сил (без составления уравнений равновесия отсеченной части конструкции): а) если сила растягивает стержень в заданном сечении, то она дает в нем  ; б) если сила стремится вращать часть конструкции вокруг сечения по ходу часовой стрелки, то она дает в этом сечении
; б) если сила стремится вращать часть конструкции вокруг сечения по ходу часовой стрелки, то она дает в этом сечении  ; в) если сила растягивает стержень в сечении с нижней стороны (для горизонтальных стержней) или с правой стороны (для вертикальных стержней), то она дает в нем
; в) если сила растягивает стержень в сечении с нижней стороны (для горизонтальных стержней) или с правой стороны (для вертикальных стержней), то она дает в нем  .
.
В дальнейшем при составлении выражений для  в заданном сечении будут везде использоваться приведенные выше правила. В заключении параграфа следует заметить, при расчете конструкции значения
в заданном сечении будут везде использоваться приведенные выше правила. В заключении параграфа следует заметить, при расчете конструкции значения  определяются не в каком-либо одном сечении, а по длине всех стержней конструкции в виде соответствующих графиков, называемых эпюрами
определяются не в каком-либо одном сечении, а по длине всех стержней конструкции в виде соответствующих графиков, называемых эпюрами  . Необходимость построения таких эпюр обусловлена не только расчетом конструкций на прочность, но и, как будет показано ниже, расчетом ее на жесткость.
. Необходимость построения таких эпюр обусловлена не только расчетом конструкций на прочность, но и, как будет показано ниже, расчетом ее на жесткость.
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК
В поперечных сечениях балок при действии нагрузки перпендикулярной их оси возникают поперечная сила 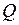 и изгибающий момент
и изгибающий момент  . Распределение
. Распределение 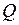 и
и  по длине балки изображается в виде соответствующих эпюр. Правильность построения эпюр
по длине балки изображается в виде соответствующих эпюр. Правильность построения эпюр 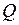 и
и  можно проверять с помощью основных дифференциальных зависимостей при изгибе. Для получения этих зависимостей рассмотрим произвольную балку (рис. 1.3а) и составим уравнения равновесия ее бесконечно малого элемента
можно проверять с помощью основных дифференциальных зависимостей при изгибе. Для получения этих зависимостей рассмотрим произвольную балку (рис. 1.3а) и составим уравнения равновесия ее бесконечно малого элемента  (рис. 1.3б).
(рис. 1.3б).
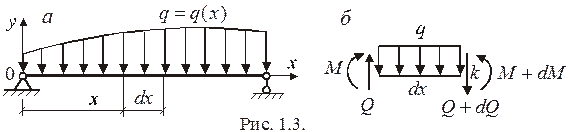
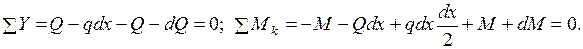
Из этих уравнений получаем дифференциальные зависимости:
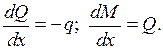
Согласно данным зависимостям на участках с 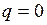
 , а
, а  меняется линейно. Причем, если
меняется линейно. Причем, если  , то
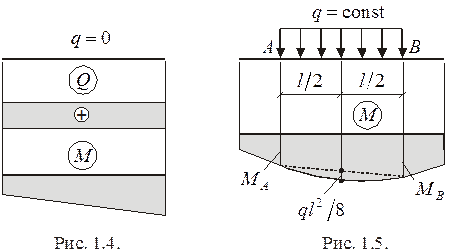
, то  линейно возрастает (рис. 1.4). Положительные ординаты эпюры
линейно возрастает (рис. 1.4). Положительные ординаты эпюры  откладываются с нижней стороны участка. Если на участке
откладываются с нижней стороны участка. Если на участке  , то
, то 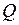 линейно убывает (при направлении
линейно убывает (при направлении  вниз), а эпюра
вниз), а эпюра  - квадратная парабола. Способ построения такой параболы показан на рис. 1.5. Причем, если есть точка, в которой
- квадратная парабола. Способ построения такой параболы показан на рис. 1.5. Причем, если есть точка, в которой  , то эпюра
, то эпюра  в этой точке имеет экстремум.
в этой точке имеет экстремум.
Рассмотрим пример построения эпюр 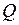 и
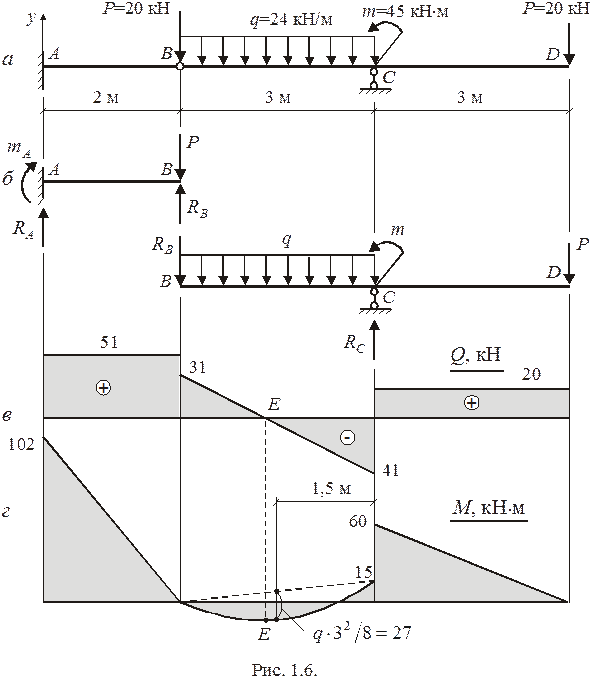
и  в статически определимой шарнирной балке (рис. 1.6а). Предварительно определим реакции опор и силы взаимодействия между частями балки (рис. 1.6б), составляя для каждой части по два уравнения равновесия.
в статически определимой шарнирной балке (рис. 1.6а). Предварительно определим реакции опор и силы взаимодействия между частями балки (рис. 1.6б), составляя для каждой части по два уравнения равновесия.
Для части BCD:
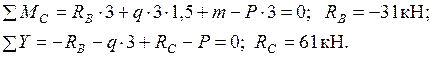
Для части AB:
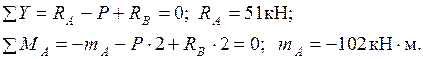
Определяем 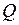 и
и  на каждом участке балки (рис. 1.6б). Направление движения по каждому участку определяется расположением букв в обозначении участка: первая буква - начало участка, вторая - конец участка. Знаки
на каждом участке балки (рис. 1.6б). Направление движения по каждому участку определяется расположением букв в обозначении участка: первая буква - начало участка, вторая - конец участка. Знаки 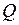 и
и  определяются по правилам, изложенным в параграфе 1.1.
определяются по правилам, изложенным в параграфе 1.1.
Участок AB: 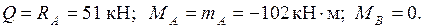
Участок BC: 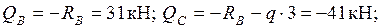
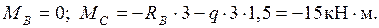
Участок DC: 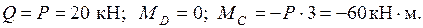
По полученным результатам строим эпюры 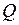 и
и  (рис. 1.6в, 1.6г). Парабола эпюры
(рис. 1.6в, 1.6г). Парабола эпюры  на участке BC строится способом, показанным на рис. 1.5. В точке E участка ВС
на участке BC строится способом, показанным на рис. 1.5. В точке E участка ВС  , а эпюра
, а эпюра  соответственно имеет экстремум.
соответственно имеет экстремум.
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ РАМ
В поперечных сечениях стержней рам в общем случае возникают три обобщенные внутренние силы:  . Расчет рамы начинается с определения реакций опор. Если рама состоит из нескольких частей, то определяются также силы взаимодействия между этими частями.
. Расчет рамы начинается с определения реакций опор. Если рама состоит из нескольких частей, то определяются также силы взаимодействия между этими частями.
Рассмотрим пример построения эпюр  и
и  в статически определимой раме, составленной из двух частей (рис. 1.7). При расположении опор А и B на одном уровне сначала целесообразно определить вертикальные реакции этих опор из двух уравнений равновесия, составленных для всей рамы:
в статически определимой раме, составленной из двух частей (рис. 1.7). При расположении опор А и B на одном уровне сначала целесообразно определить вертикальные реакции этих опор из двух уравнений равновесия, составленных для всей рамы:

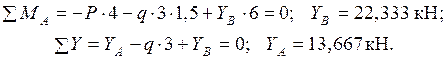
Для определения реакции  и сил в шарнире C расчленим раму на две части (рис. 1.8) и рассмотрим равновесие правой части:
и сил в шарнире C расчленим раму на две части (рис. 1.8) и рассмотрим равновесие правой части:

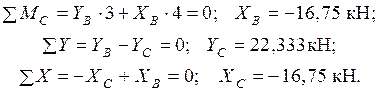
Реакция  определяется из уравнения равновесия для всей системы:
определяется из уравнения равновесия для всей системы:
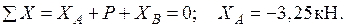
Определяем  и
и  на каждом участке рамы (рис. 1.8). При записи участков первая буква означает снова начало участка, вторая - конец участка. Знаки
на каждом участке рамы (рис. 1.8). При записи участков первая буква означает снова начало участка, вторая - конец участка. Знаки  и
и  определяются по правилам, изложенным в параграфе 1.1.
определяются по правилам, изложенным в параграфе 1.1.
Участок АЕ: 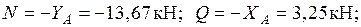

Участок СЕ: 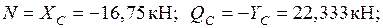

Участок СD: 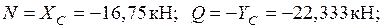
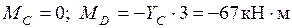 .
.
Участок BD: 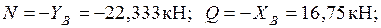
 .
.
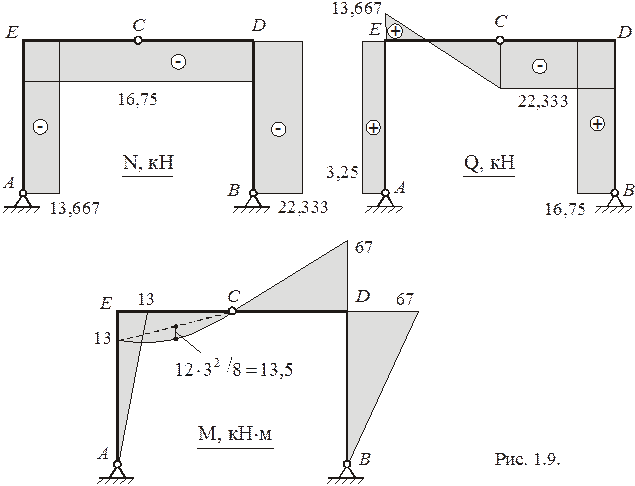
По полученным результатам строим эпюры N, Q, M (рис. 1.9). Правильность построения эпюр проверяется с помощью зависимостей 
 а также проверкой равновесия узлов. Внутренние силы N, Q, M в сечениях вокруг узлов удобнее прикладывать в действительных направлениях (рис. 1.10).
а также проверкой равновесия узлов. Внутренние силы N, Q, M в сечениях вокруг узлов удобнее прикладывать в действительных направлениях (рис. 1.10).
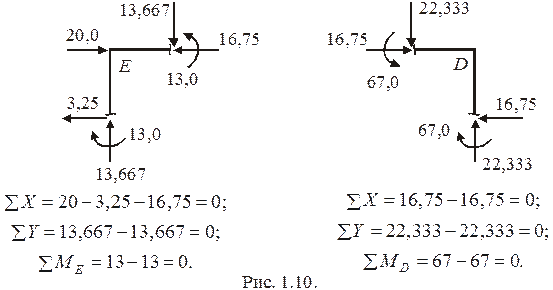
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ ФЕРМ
В поперечных сечениях стержней ферм при действии нагрузки, приложенной в их узлах, возникают только продольные силы 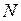 . Для определения этих сил используются два основных способа.
. Для определения этих сил используются два основных способа.
а) Способ вырезания узлов.
Суть данного способа заключается в вырезании узлов фермы и составлении уравнений равновесия этих узлов. Узлы фермы должны вырезаться в такой последовательности, чтобы в каждом из них действовало не более двух неизвестных сил для плоских ферм и не более трех неизвестных сил для пространственных ферм. Предполагается, что все стержни фермы растянуты. Поэтому силы в стержнях направляются от узлов фермы. Перед вырезанием узлов необходимо определить реакции опор из уравнений равновесия, составленных для всей фермы.
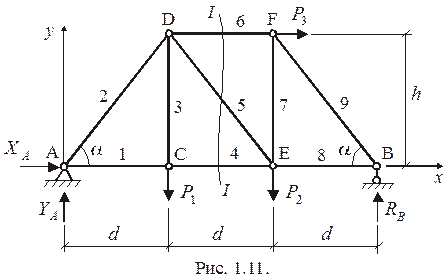
Пример (рис. 1.11).
Дано: 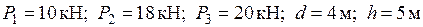 .
.
Определить:  .
.
Решение.
Реакции опор определяются из уравнений равновесия, составленных для всей фермы:
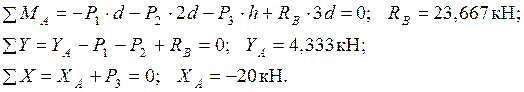
Далее вырезаем последовательно узлы и составляем уравнения равновесия сил, действующих в этих узлах.
Узел А.




Узел B.
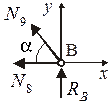

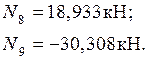
Узел С.


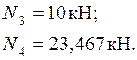
Узел F.


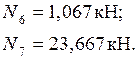
Узел D.
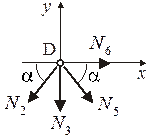
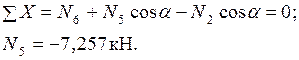
Общее число уравнений равновесия вместе с тремя уравнениями, составленными для всей фермы, должно быть равно  , где
, где  - число узлов фермы. Поэтому при вырезании всегда остаются незадействованными три уравнения равновесия (в данном случае одно уравнение для узла D и два уравнения для узла E), которые можно использовать в качестве проверочных уравнений.
- число узлов фермы. Поэтому при вырезании всегда остаются незадействованными три уравнения равновесия (в данном случае одно уравнение для узла D и два уравнения для узла E), которые можно использовать в качестве проверочных уравнений.
б) Способ сквозных сечений.
Суть данного способа заключается в составлении уравнений равновесия для части фермы, расположенной с какой-либо стороны от сквозного сечения, проведенного через интересующие стержни фермы. Сечение должно разрезать не более трех стержней.
Определим данным способом силы в стержнях 4, 5, 6 прежней фермы (рис. 1.11). Для этого проведем через данные стержни сквозное сечение I-I и рассмотрим равновесие части фермы, расположенной с левой стороны от проведенного сечения (рис. 1.12). Каждую из сил  можно определить независимо от двух других сил:
можно определить независимо от двух других сил:

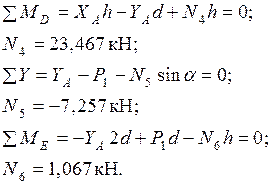
Полученные значения 
 совпадают с теми, что были найдены ранее способом вырезания узлов.
совпадают с теми, что были найдены ранее способом вырезания узлов.
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ АРОК
В поперечных сечениях арок возникают три внутренние силы:  . Рассмотрим процедуру определения этих сил на примере трехшарнирой арки (рис. 1.13). Исходные данные:
. Рассмотрим процедуру определения этих сил на примере трехшарнирой арки (рис. 1.13). Исходные данные:  .
.
Определяем реакции опор:
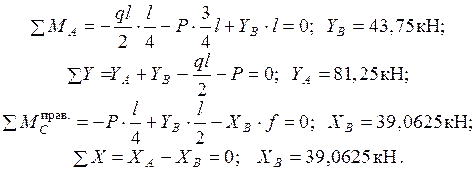
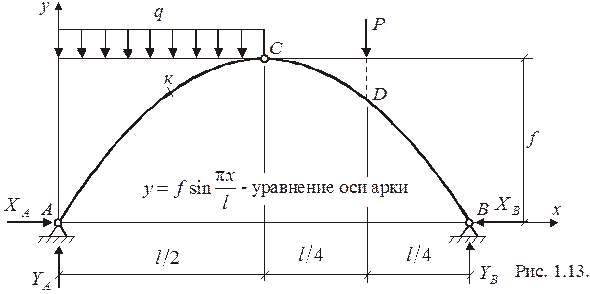
Внутренние силы  на участке АС (
на участке АС (  ) определяем способом сечений, составляя три уравнения равновесия для части, расположенной с левой стороны от проведенного сечения (рис. 1.14):
) определяем способом сечений, составляя три уравнения равновесия для части, расположенной с левой стороны от проведенного сечения (рис. 1.14):

Из этих уравнений получаем


На остальных участках выражения для  можно записать, используя соответствующие выражения на предыдущем участке. При этом следует рассматривать всегда часть арки, расположенную слева от текущего сечения, а начало отсчета брать в точке А.
можно записать, используя соответствующие выражения на предыдущем участке. При этом следует рассматривать всегда часть арки, расположенную слева от текущего сечения, а начало отсчета брать в точке А.
Участок CD:
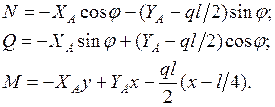
Участок DB:

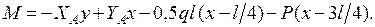
Функции  определяются по уравнению оси арки:
определяются по уравнению оси арки:
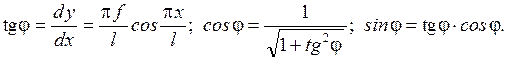
Результаты расчета приведены в таблице 1.1 и на рис. 1.15.
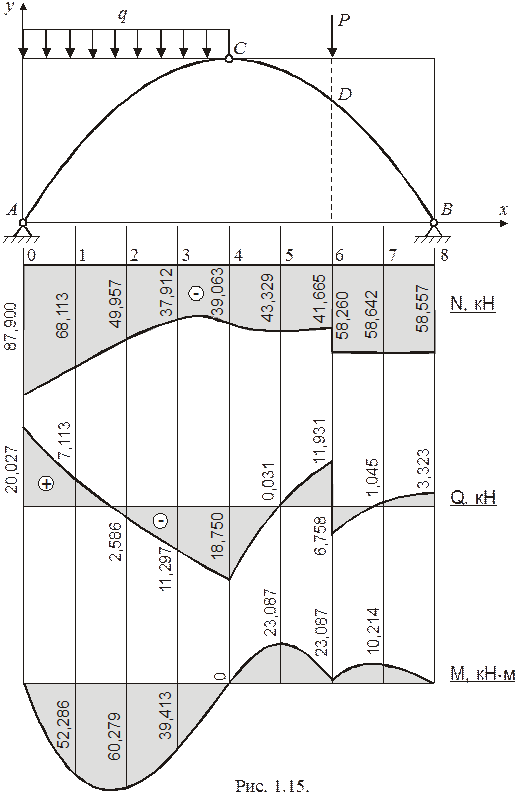
Таблица 1.1.
| № | 
| 
| 
| 
| 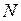
| 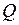
| 
|
| - | м | м | - | - | кН | кН | кН м |
| 0,0 | 0,0 | 0,782 | 0,623 | -87,900 | 20,027 | 0,0 | |
| 2,5 | 3,061 | 0,758 | 0,653 | -68,113 | 7,113 | 52,286 | |
| 5,0 | 5,657 | 0,664 | 0,748 | -49,957 | -2,586 | 60,279 | |
| 7,5 | 7,391 | 0,433 | 0,901 | -37,912 | -11,297 | 39,413 | |
| 10,0 | 8,0 | 0,0 | 1,0 | -39,063 | -18,750 | 0,0 | |
| 12,5 | 7,391 | -0,433 | 0,901 | -43,329 | 0,031 | -23,087 | |
| 15,0 | 5,657 | -0,664 | 0,748 | -41,655/-58,260 | 11,931/-6,758 | -2,221 | |
| 17,5 | 3,061 | -0,758 | 0,653 | -58,642 | 1,045 | -10,214 | |
| 20,0 | 0,0 | -0,782 | 0,623 | -58,557 | 3,323 | 0,0 |
Дата добавления: 2014-11-13; просмотров: 404; Мы поможем в написании вашей работы!; Нарушение авторских прав |