
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
СТЕПЕНЬ КИНЕМАТИЧЕСКОЙ НЕОПРЕДЕЛИМОСТИ
ПЛОСКОЙ СТЕРЖНЕВОЙ СИСТЕМЫ
В методе перемещений неизвестными параметрами являются обобщенные перемещения узлов конструкции: в шарнирных узлах определяются линейные перемещения; в жестких узлах кроме линейных перемещений определяются также их углы поворота. Степенью кинематической неопределимости (СКН) называется общее число неизвестных углов поворота и независимых линейных перемещений узлов конструкции. Для плоских стержневых систем СКН определяется по формуле  , где
, где  - число жестких узлов;
- число жестких узлов;  - число независимых линейных перемещений всех узлов системы.
- число независимых линейных перемещений всех узлов системы.
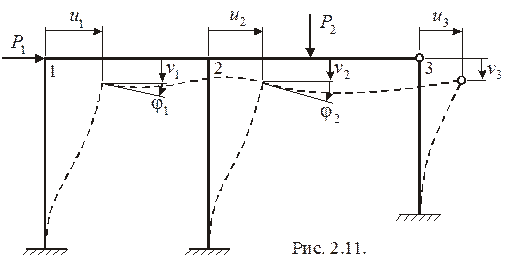
На рис. 2.11 показана плоская рама с неизвестными обобщенными перемещениями  , для которой
, для которой  Таким образом
Таким образом  , что представляет достаточно большую величину.
, что представляет достаточно большую величину.
С целью уменьшения СКН при расчете рам в методе перемещений вводятся два допущения, несущественно влияющие на результаты расчета: 1) считается, что в продольном направлении стержни являются абсолютно жесткими (  ); 2) считается, что проекция изогнутого стержня на его недеформированную ось равна начальной длине стержня. Первое из этих допущений уже принималось ранее при определении перемещений в рамах, а второе допущение обусловлено малостью перемещений по сравнению с размерами конструкции (принцип геометрической неизменяемости системы).
); 2) считается, что проекция изогнутого стержня на его недеформированную ось равна начальной длине стержня. Первое из этих допущений уже принималось ранее при определении перемещений в рамах, а второе допущение обусловлено малостью перемещений по сравнению с размерами конструкции (принцип геометрической неизменяемости системы).
С учетом данных допущений для рассмотренной рамы имеем: 
 . Таким образом
. Таким образом  , а СКН=3, что существенно меньше по сравнению с начальным результатом.
, а СКН=3, что существенно меньше по сравнению с начальным результатом.
ОСНОВНАЯ СИСТЕМА МЕТОДА ПЕРЕМЕЩЕНИЙ
Основная система (ОС) метода перемещений получается из заданной системы путем введения в нее дополнительных связей: в жестких узлах вводятся заделки, препятствующие повороту данных узлов; кроме того, вводятся опорные стержни, препятствующие независимым линейным перемещениям узлов. Число заделок равно  , число дополнительных опорных стержней равно
, число дополнительных опорных стержней равно  . По направлениям дополнительных связей указываются неизвестные обобщенные перемещения узлов, которые далее будут обозначаться как
. По направлениям дополнительных связей указываются неизвестные обобщенные перемещения узлов, которые далее будут обозначаться как 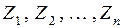
 . В отличие от метода сил, в методе перемещений из заданной системы можно получить только одну ОС. На рис. 2.12 приведены примеры получения ОС метода перемещений.
. В отличие от метода сил, в методе перемещений из заданной системы можно получить только одну ОС. На рис. 2.12 приведены примеры получения ОС метода перемещений.
КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА ПЕРЕМЕЩЕНИЙ
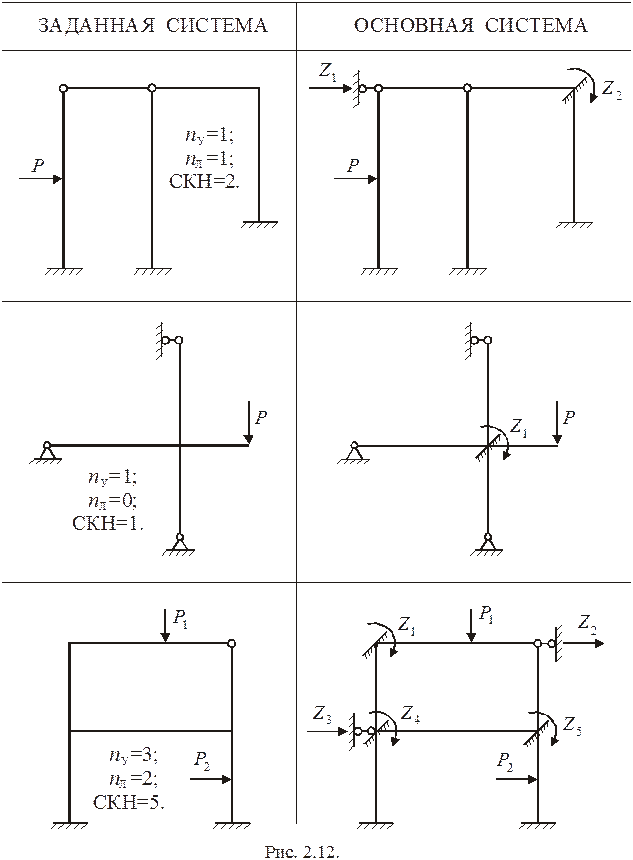
Неизвестные перемещения 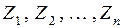 определяются из условий отсутствия реакций дополнительных связей в ОС, возникающих совместно от этих перемещений и заданной нагрузки. Эти условия записываются в виде канонических уравнений метода перемещений. Рассмотрим получение данных уравнений на примере системы, имеющей
определяются из условий отсутствия реакций дополнительных связей в ОС, возникающих совместно от этих перемещений и заданной нагрузки. Эти условия записываются в виде канонических уравнений метода перемещений. Рассмотрим получение данных уравнений на примере системы, имеющей  (рис. 2.13).
(рис. 2.13).
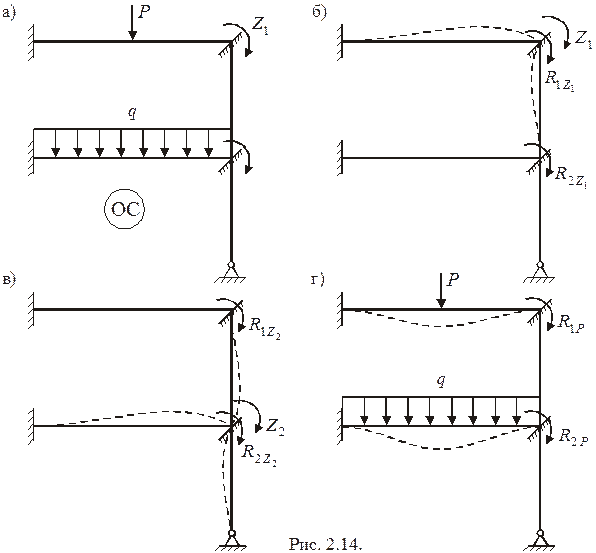
На рис. 2.14а показана ОС с неизвестными перемещениями 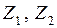 и заданной нагрузкой. Заданная система, как и прежде, считается линейно-деформируемой. Тогда исходное состояние ОС можно разложить на три независимых состояния: состояние от перемещения
и заданной нагрузкой. Заданная система, как и прежде, считается линейно-деформируемой. Тогда исходное состояние ОС можно разложить на три независимых состояния: состояние от перемещения 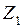 (рис. 2.14б); состояние от перемещения
(рис. 2.14б); состояние от перемещения 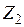 (рис. 2.14в) и состояние от нагрузки (рис. 2.14г). В каждом из этих состояний элементы ОС определенным образом деформируются и поэтому в узлах, где введены дополнительные связи, возникают реакции данных связей: от перемещения
(рис. 2.14в) и состояние от нагрузки (рис. 2.14г). В каждом из этих состояний элементы ОС определенным образом деформируются и поэтому в узлах, где введены дополнительные связи, возникают реакции данных связей: от перемещения 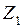 - реакции
- реакции 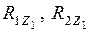 ; от перемещения
; от перемещения  - реакции
- реакции  и от нагрузки - реакции
и от нагрузки - реакции  . Положительные направления отмеченных реакций совпадают с направлениями соответствующих неизвестных перемещений
. Положительные направления отмеченных реакций совпадают с направлениями соответствующих неизвестных перемещений 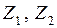 .
.
 Чтобы ОС была эквивалентной заданной системе, алгебраическая сумма реакций дополнительных связей в направлении каждого неизвестного перемещения должна быть равна нулю (в заданной системе дополнительные связи отсутствуют):
Чтобы ОС была эквивалентной заданной системе, алгебраическая сумма реакций дополнительных связей в направлении каждого неизвестного перемещения должна быть равна нулю (в заданной системе дополнительные связи отсутствуют):
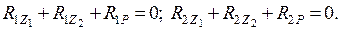
В линейно-деформируемой системе реакции дополнительных связей от перемещений 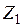
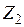 прямо пропорциональны этим перемещениям:
прямо пропорциональны этим перемещениям: 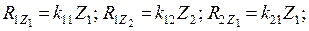
 Каждый коэффициент пропорциональности
Каждый коэффициент пропорциональности  есть реакция дополнительной связи в направлении перемещения
есть реакция дополнительной связи в направлении перемещения 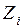 от перемещения
от перемещения  . Поэтому коэффициенты
. Поэтому коэффициенты  называются коэффициентами жесткости.
называются коэффициентами жесткости.
Подставляя последние соотношения в предыдущие равенства, получаем канонические уравнения для случая  :
:
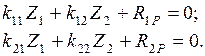
Данные уравнения можно обобщить на случай  :
:
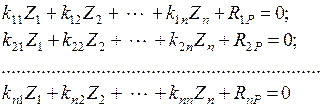
или в матричной форме:
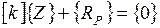 .
.
Здесь
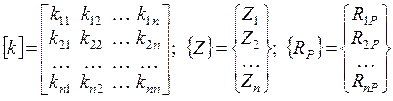
представляют соответственно матрицу жесткости, вектор неизвестных перемещений и вектор свободных членов канонических уравнений.
Свойства матрицы жесткости. Матрица  всегда является симметричной (
всегда является симметричной (  ) и положительно определенной (
) и положительно определенной (  ).
).
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ПРИ НЕИЗВЕСТНЫХ
И СВОБОДНЫХ ЧЛЕНОВ КАНОНИЧЕСКИХ УРАВНЕНИЙ
Коэффициенты при неизвестных (коэффициенты жесткости)  и свободные члены
и свободные члены  канонических уравнений по физическому смыслу представляют реакции дополнительных связей в ОС в направлениях неизвестных перемещений
канонических уравнений по физическому смыслу представляют реакции дополнительных связей в ОС в направлениях неизвестных перемещений  . Поэтому их можно определить из равновесия узлов или частей ОС, содержащих дополнительные связи. С этой целью в ОС строятся эпюры
. Поэтому их можно определить из равновесия узлов или частей ОС, содержащих дополнительные связи. С этой целью в ОС строятся эпюры  от перемещений
от перемещений  и эпюра
и эпюра  от нагрузки.
от нагрузки.
Дополнительные связи делят ОС на типовые элементы - однопролетные статически неопределимые балки. При расчете плоских рам встречаются элементы двух типов (рис. 2.15).
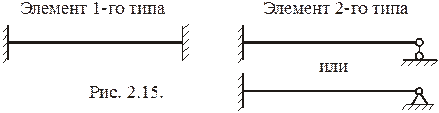
Эпюры изгибающих моментов от единичных перемещений и нагрузки в указанных типовых элементах берутся из справочных данных (см. таблицу 2.1). Направления реакций в справочных данных указаны действительными.
Пример определения  и
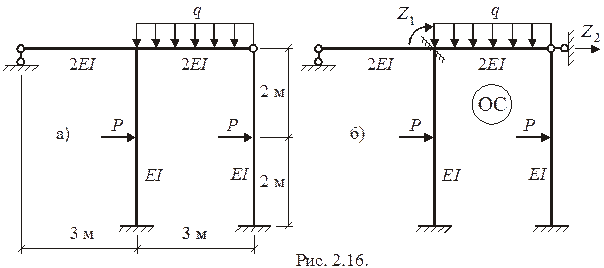
и  для плоской рамы (рис. 2.16а).
для плоской рамы (рис. 2.16а).
В заданной раме 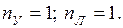 Отсюда
Отсюда  . Основная система (рис. 2.16б) содержит два неизвестных перемещения, определяемые из канонических уравнений
. Основная система (рис. 2.16б) содержит два неизвестных перемещения, определяемые из канонических уравнений
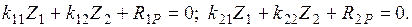
Для определения коэффициентов при неизвестных  и свободных членов
и свободных членов  этих уравнений строим в ОС эпюры
этих уравнений строим в ОС эпюры  (рис. 2.17а, 2.17б, 2.17в) соответственно от перемещений
(рис. 2.17а, 2.17б, 2.17в) соответственно от перемещений 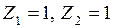 и заданной нагрузки с использованием справочных данных, приведенных в таблице 2.1. Коэффициенты жесткости
и заданной нагрузки с использованием справочных данных, приведенных в таблице 2.1. Коэффициенты жесткости  и реакция
и реакция  определяются согласно их физическому смыслу из равновесия моментов в узле, содержащем первую дополнительную связь (рис. 2.18). Для определения
определяются согласно их физическому смыслу из равновесия моментов в узле, содержащем первую дополнительную связь (рис. 2.18). Для определения  и
и  рассматривается равновесие сил в части ОС, содержащей вторую дополнительную связь (рис. 2.18). Необходимые для этого поперечные силы в поперечных сечениях стоек проще всего определять как производные от изгибающих моментов. Направления этих сил можно определить по правилу: если в каком-либо сечении ось стержня стремится поворачиваться при совмещении с касательной к эпюре моментов по часовой стрелке, то в этом сечении
рассматривается равновесие сил в части ОС, содержащей вторую дополнительную связь (рис. 2.18). Необходимые для этого поперечные силы в поперечных сечениях стоек проще всего определять как производные от изгибающих моментов. Направления этих сил можно определить по правилу: если в каком-либо сечении ось стержня стремится поворачиваться при совмещении с касательной к эпюре моментов по часовой стрелке, то в этом сечении  . Если поперечная сила в сечении стержня определяется от действия нагрузки на данном стержне, то она направляется по этой нагрузке.
. Если поперечная сила в сечении стержня определяется от действия нагрузки на данном стержне, то она направляется по этой нагрузке.
По рис. 2.18 получаем: 
 .
.
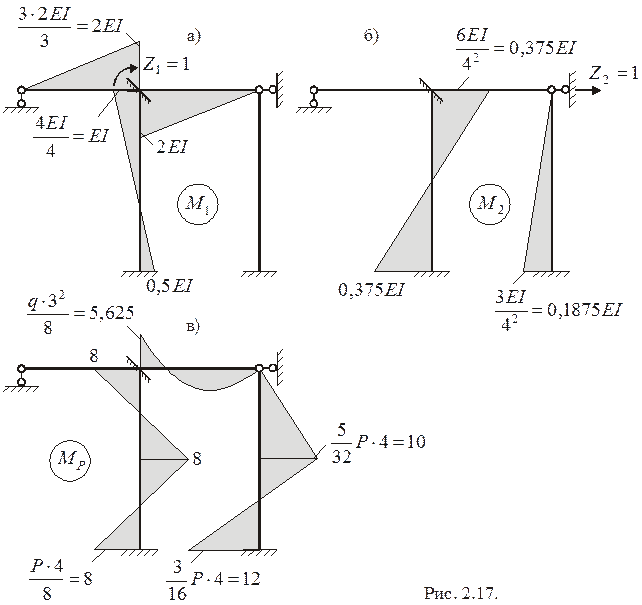
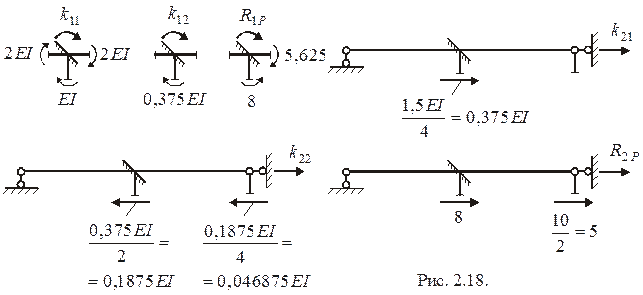
Таблица 2.1. Справочные данные для типовых элементов.
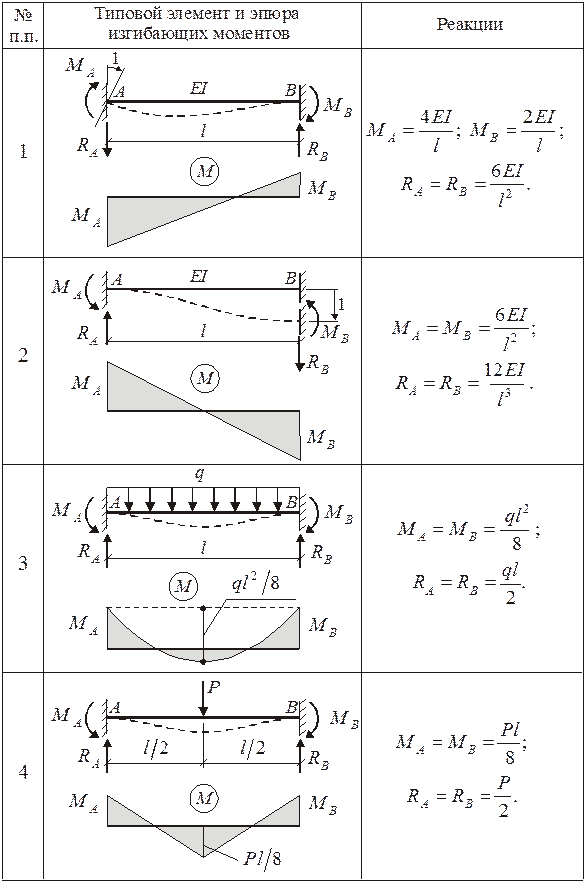
Продолжение таблицы 2.1.
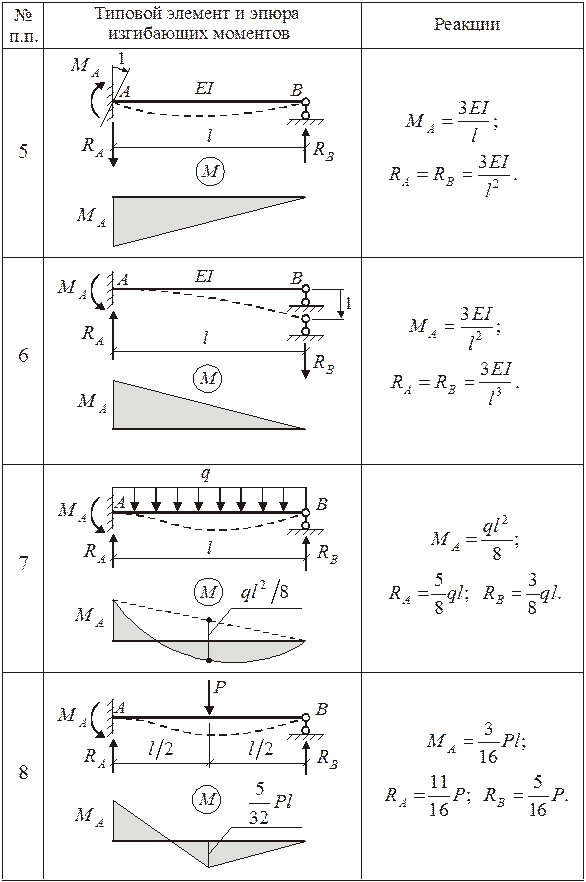
ОПРЕДЕЛЕНИЕ ОБОБЩЕННЫХ ВНУТРЕННИХ
СИЛ В ЗАДАННОЙ СИСТЕМЕ
 После определения из канонических уравнений перемещений
После определения из канонических уравнений перемещений  сначала строится эпюра
сначала строится эпюра  . Для этого используется известный принцип суперпозиции:
. Для этого используется известный принцип суперпозиции:  . Поперечные силы
. Поперечные силы 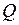 можно определить из равновесия участков конструкции. Рассмотрим один такой участок, на котором действует постоянная распределенная нагрузка
можно определить из равновесия участков конструкции. Рассмотрим один такой участок, на котором действует постоянная распределенная нагрузка  (рис. 2.19). Направление
(рис. 2.19). Направление  вниз считается положительным. Изгибающие моменты
вниз считается положительным. Изгибающие моменты 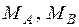 по краям участка находятся по эпюре
по краям участка находятся по эпюре  (рис. 2.19 эти моменты и изображены в положительных направлениях). Так как
(рис. 2.19 эти моменты и изображены в положительных направлениях). Так как  , то достаточно определить значения
, то достаточно определить значения 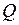 по краям участка, составляя для этого два уравнения равновесия:
по краям участка, составляя для этого два уравнения равновесия:
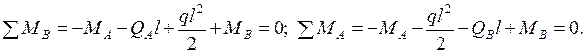
Из этих уравнений получаем поперечные силы 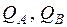 (на рис. 2.19 направления этих сил являются положительными):
(на рис. 2.19 направления этих сил являются положительными):
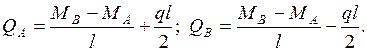
Моменты 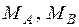 следует подставлять в эти формулы с учетом их знаков. При
следует подставлять в эти формулы с учетом их знаков. При  формулы для
формулы для 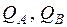 дают на участке
дают на участке 
 . Данные формулы справедливы и для вертикальных участков, если рис. 2.19 повернуть на
. Данные формулы справедливы и для вертикальных участков, если рис. 2.19 повернуть на  против хода часовой стрелки.
против хода часовой стрелки.
Продольные силы 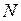 в стержнях определяются по известным поперечным силам
в стержнях определяются по известным поперечным силам 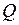 из равновесия узлов конструкции. Правильность построения эпюр
из равновесия узлов конструкции. Правильность построения эпюр  проверяется составлением уравнений равновесия для всей конструкции. Необходимые для этого реакции опор и их действительные направления можно определить непосредственно по эпюрам
проверяется составлением уравнений равновесия для всей конструкции. Необходимые для этого реакции опор и их действительные направления можно определить непосредственно по эпюрам  .
.
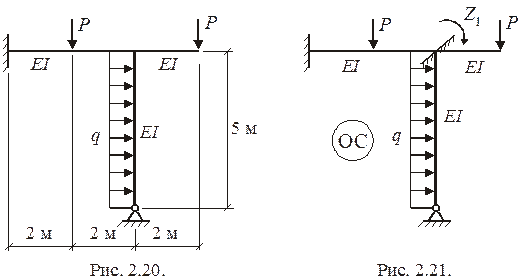
Пример расчета статически неопределимой
рамы (рис.2.20) методом перемещений.
Дано:  . Построить эпюры
. Построить эпюры 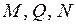 .
.
1. Определение СКН и получение ОС
В заданной раме  Отсюда
Отсюда  . Основная система (рис. 2.21) получается из заданной путем введения одной дополнительной связи - заделки в жестком узле конструкции. Неизвестное обобщенное перемещение (угол поворота данного узла)
. Основная система (рис. 2.21) получается из заданной путем введения одной дополнительной связи - заделки в жестком узле конструкции. Неизвестное обобщенное перемещение (угол поворота данного узла)  определяется из канонического уравнения
определяется из канонического уравнения
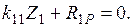
2. Построение эпюр  ,
,  в ОС
в ОС
Эпюры  и
и  (рис. 2.22, рис. 2.23) строятся в ОС соответственно от перемещения
(рис. 2.22, рис. 2.23) строятся в ОС соответственно от перемещения 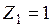 и нагрузки по справочным данным для типовых элементов метода перемещений (табл. 2.1).
и нагрузки по справочным данным для типовых элементов метода перемещений (табл. 2.1).
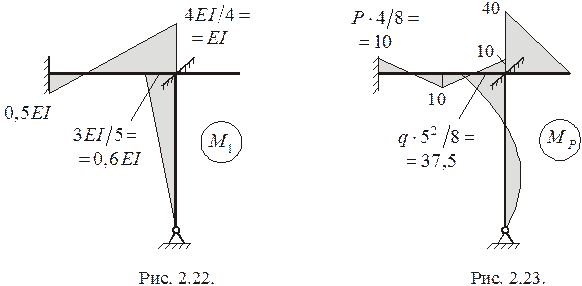
3. Определение  и перемещения
и перемещения 
Коэффициент 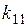 и свободный член
и свободный член  канонического уравнения представляют реакции дополнительной связи в направлении
канонического уравнения представляют реакции дополнительной связи в направлении  соответственно от
соответственно от  перемещения
перемещения 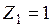 и заданной нагрузки. Поэтому их можно определить из равновесия внешних и внутренних моментов в узле ОС, содержащем дополнительную связь (рис. 2.24):
и заданной нагрузки. Поэтому их можно определить из равновесия внешних и внутренних моментов в узле ОС, содержащем дополнительную связь (рис. 2.24):  ;
;  . Перемещение
. Перемещение  определяется из канонического уравнения:
определяется из канонического уравнения: 
 .
.
4. Построение эпюр 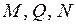 в заданной системе
в заданной системе
Эпюра  (рис. 2.25а) строится по принципу суперпозиции:
(рис. 2.25а) строится по принципу суперпозиции: 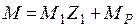 .
.
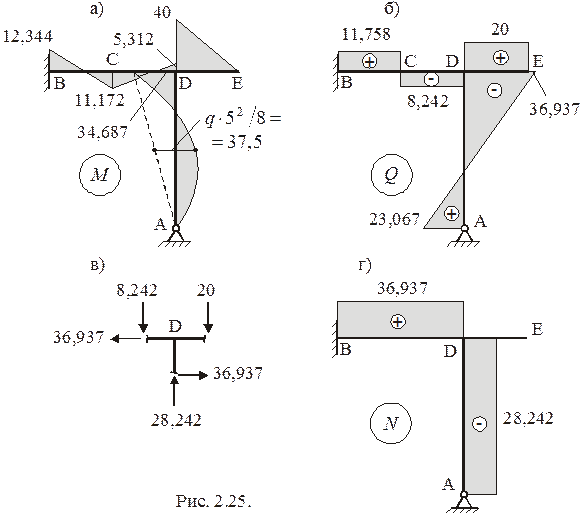
Поперечные силы на участках конструкции определяются по известным изгибающим моментам с использованием полученных выше формул:
Участок BC: 
Участок CD: 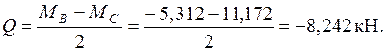
Участок DE: 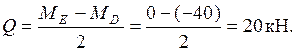
Участок AD: 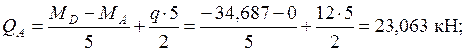
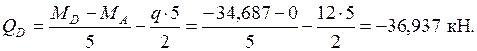
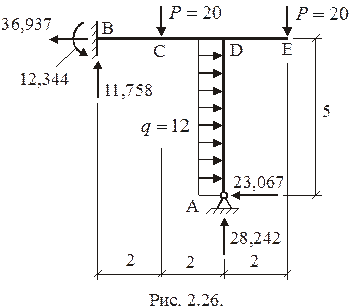 По полученным результатам строится эпюра
По полученным результатам строится эпюра  (рис. 25б). Продольные силы
(рис. 25б). Продольные силы  в стержнях определяются по известным поперечным силам
в стержнях определяются по известным поперечным силам  из равновесия узла D рамы (рис. 25в). Направления
из равновесия узла D рамы (рис. 25в). Направления 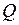 и
и 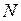 в сечениях вокруг узла берутся действительными. Эпюра
в сечениях вокруг узла берутся действительными. Эпюра 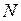 показана на рис. 25г. Правильность расчета проверяется с помощью уравнений равновесия для всей конструкции (рис. 2.26). Необходимые для этого реакции опор и их действительные направления определяются непосредственно по эпюрам
показана на рис. 25г. Правильность расчета проверяется с помощью уравнений равновесия для всей конструкции (рис. 2.26). Необходимые для этого реакции опор и их действительные направления определяются непосредственно по эпюрам  .
.
Дата добавления: 2014-11-13; просмотров: 1449; Мы поможем в написании вашей работы!; Нарушение авторских прав |