
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВВЕДЕНИЕ. Любая конструкция или сооружение должны быть прочными, жесткими и устойчивыми, т.е
ПРЕДМЕТ СТРОИТЕЛЬНОЙ МЕХАНИКИ
Любая конструкция или сооружение должны быть прочными, жесткими и устойчивыми, т.е. они не должны разрушаться от действия внешних сил и иметь необходимый запас прочности; в них недопустимы перемещения, нарушающую их нормальную эксплуатацию; кроме того, должна быть исключена возможная потеря устойчивости заданной формы равновесия. Строительная механика занимается разработкой методов статических и динамических расчетов конструкций и сооружений на прочность, жесткость и устойчивость. Статика сооружений изучает их работу при статическом действии нагрузки - медленном ее изменении в определенном интервале времени. При динамическом действии нагрузки, быстро меняющейся во времени, учитываются динамические эффекты нагрузки и вводятся в рассмотрение силы инерции.
ОСНОВНАЯ ЗАДАЧА СТРОИТЕЛЬНОЙ МЕХАНИКИ
В классическом курсе строительной механики рассматриваются в основном стержневые системы. Основная задача строительной механики состоит в определении обобщенных внутренних сил в поперечных сечениях стержней от заданных внешних воздействий. В дальнейшем будут рассматриваться только плоские стержневые системы. В поперечных сечениях стержней таких систем в общем случае возникают три обобщенные внутренние силы: продольная сила N; поперечная сила Q; изгибающий момент M (рис. 0.1).

Правила знаков для N, Q, M:
а) N>0 растягивает ось стержня;
б) Q>0 стремится вращать любую часть конструкции по часовой стрелке;
в) M>0 растягивает нижнюю сторону стержня (для вертикальных стержней - правую сторону).
По известным внутренним силам N, Q, M, используя формулы сопротивления материалов, можно определить нормальные  и касательные напряжения
и касательные напряжения  , необходимые при прочностном расчете конструкции. Наличие N, Q, M позволяет также определить перемещения характерных точек конструкции, необходимые для ее расчета на жесткость.
, необходимые при прочностном расчете конструкции. Наличие N, Q, M позволяет также определить перемещения характерных точек конструкции, необходимые для ее расчета на жесткость.
ПОНЯТИЕ О РАСЧЕТНОЙ СХЕМЕ КОНСТРУКЦИИ
Реальная строительная конструкция представляет сложную совокупность различных по назначению и виду элементов, а нагрузка, действующая на конструкцию, представляет сложную систему сил. Определение напряженно-деформированного состояния конструкции с учетом всех ее конструктивных и силовых особенностей в большинстве случаев представляет практически невыполнимую задачу. Поэтому при расчете любой конструкции всегда необходимо переходить к некоторой упрощенной модели, учитывающей только основные конструктивные и силовые свойства реальной конструкции, и вместе с тем дающую необходимую для практики точность расчета. Такая упрощенная модель называется расчетной схемой (РС) конструкции.
Выбор РС - сложный и многогранный вопрос, зависящий не только от вида конструкции, но и от нагрузки, действующей на нее, требуемой точности, цели расчета (проектировочного или проверочного), соотношения жесткостей элементов конструкции, имеющихся в распоряжении вычислительных средств и т.д. Учет большого числа факторов, влияющих на конечный результат, не всегда целесообразен, так как увеличивает трудоемкость расчета. В то же время чрезмерное упрощение реальной конструкции может привести к неудовлетворительным результатам. Поэтому удачный выбор РС представляет достаточно сложный и ответственный этап расчета конструкции.
На рис. 0.2 показан пример расчетной схемы фермы, в которой все стержни соединяются шарнирами (в действительности соединение стержней в узлах жесткое), а силы приложены в узлах. Тогда в каждом стержне фермы из трех обобщенных внутренних сил 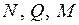 будет иметься только продольная сила
будет иметься только продольная сила  , что существенно упрощает расчет фермы.
, что существенно упрощает расчет фермы.

ГЕОМЕТРИЧЕСКИ ИЗМЕНЯЕМЫЕ
И НЕИЗМЕНЯЕМЫЕ СИСТЕМЫ
Любая конструкция и сооружение должны быть геометрически неизменяемыми, т.е. они должны сохранять геометрическую форму, заданную при изготовлении (возведении). Изменяемые системы в качестве конструкций и сооружений недопустимы, т.к. они меняют форму, получая перемещения без деформации их элементов. Примером простейшей геометрически неизменяемой системы (ГНС) является шарнирный треугольник (рис. 0.3а). Шарнирный четырехугольник (рис. 0.3б) - пример геометрически изменяемой системы (ГИС).

Критерием, по которому можно судить о геометрической неизменяемости или изменяемости системы, является ее число степеней свободы W (число независимых геометрических параметров, определяющих положение всех элементов системы). На рис. 0.4 показаны простейшие объекты: материальная точка A в плоскости и линейный объект AB в плоскости (диск), которые соответственно имеют  и
и  .
.

Опорный стержень отнимает у любого материального объекта одну степень свободы (рис. 0.5).

Жесткая заделка в плоскости отнимает у тела три степени свободы (рис. 0.6).

Для произвольной плоской системы, составленной из жестких дисков, соединенными между собой шарнирами и прикрепленными к “земле” опорными связями, число степеней свободы определяется по формуле
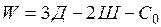 ,
,
где  - число жестких дисков;
- число жестких дисков;  - число простых (соединяющих два диска) шарниров, если шарнир соединяет число дисков
- число простых (соединяющих два диска) шарниров, если шарнир соединяет число дисков  , то в этом случае
, то в этом случае 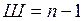 ;
;  - число элементарных опорных связей. На рис. 0.7 приведены три типа опорных связей в плоскости и соответствующие им значения
- число элементарных опорных связей. На рис. 0.7 приведены три типа опорных связей в плоскости и соответствующие им значения  .
.

При определении W ферм удобнее пользоваться формулами:
 - для плоских ферм;
- для плоских ферм;
 - для пространственных ферм.
- для пространственных ферм.
Здесь  - число узлов;
- число узлов;  - число стержней фермы;
- число стержней фермы;  - число элементарных опорных связей.
- число элементарных опорных связей.
На рис. 0.8 показаны некоторые плоские системы и определены значения числа степеней свободы  этих систем. На основании анализа приведенных результатов видно, что при
этих систем. На основании анализа приведенных результатов видно, что при  система может быть неизменяемой (рис. 0.8а, 0.8б), но может быть и изменяемой (рис. 0.8в, 0.8д). Поэтому условие
система может быть неизменяемой (рис. 0.8а, 0.8б), но может быть и изменяемой (рис. 0.8в, 0.8д). Поэтому условие  не является достаточным условием геометрической неизменяемости системы, а только лишь необходимым. При
не является достаточным условием геометрической неизменяемости системы, а только лишь необходимым. При  заключение о неизменяемости или изменяемости системы возможно только после анализа ее структуры: любая сложная геометрически неизменяемая система должна получаться последовательным соединением ее частей в соответствии с принципами образования простейших геометрически неизменяемых систем. При
заключение о неизменяемости или изменяемости системы возможно только после анализа ее структуры: любая сложная геометрически неизменяемая система должна получаться последовательным соединением ее частей в соответствии с принципами образования простейших геометрически неизменяемых систем. При  система всегда является геометрически изменяемой (рис. 0.8г).
система всегда является геометрически изменяемой (рис. 0.8г).
На рис. 0.9 показаны принципы образования простейших геометрически неизменяемых систем (точки A, B, C не должны располагаться на одной прямой).
Геометрически неизменяемые системы, в которых  , являются статически определимыми. Для определения реакций опор и обобщенных внутренних сил в таких системах достаточно использовать только лишь уравнения равновесия.
, являются статически определимыми. Для определения реакций опор и обобщенных внутренних сил в таких системах достаточно использовать только лишь уравнения равновесия.


Геометрически неизменяемые системы, в которых  , являются статически неопределимыми. В таких системах число элементарных связей превышает число независимых уравнений равновесия на величину “ –W “, которая называется степенью статической неопределимости (ССН) системы. Для расчета таких систем кроме уравнений равновесия необходимо использовать еще дополнительные уравнения, вытекающие из условий совместности перемещений некоторых точек системы и налагаемых на них связей.
, являются статически неопределимыми. В таких системах число элементарных связей превышает число независимых уравнений равновесия на величину “ –W “, которая называется степенью статической неопределимости (ССН) системы. Для расчета таких систем кроме уравнений равновесия необходимо использовать еще дополнительные уравнения, вытекающие из условий совместности перемещений некоторых точек системы и налагаемых на них связей.
На рис. 0.10 показаны примеры статически определимой и статически неопределимой систем.
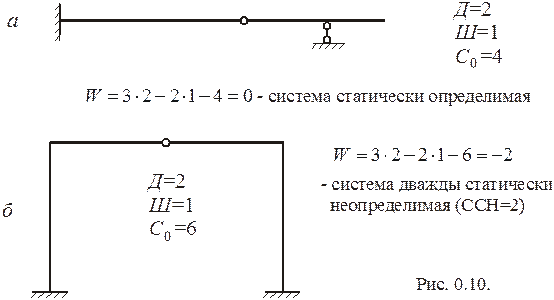
Имеются системы, которые являются изменяемыми только в каком-то одном положении, а при небольшом отклонении от этого положения становятся неизменяемыми. Такие системы являются мгновенно изменяемыми и в качестве конструкций не используются, т.к. в них могут возникать неопределенно большие реакции и внутренние силы. Простейшие мгновенно изменяемые системы показаны на рис. 0.11.

Дата добавления: 2014-11-13; просмотров: 612; Мы поможем в написании вашей работы!; Нарушение авторских прав |