Научные основы современных рядов предпочтительных чисел

Научные основы современных рядов предпочтительных чисел, основанных на геометрической прогрессии, были разработаны в 1877-1879 гг. офицером французского инженерного корпуса Шарлем Ренаром. Он разработал спецификацию на диаметры хлопчатобумажных канатов для аэростатов и воздушных шаров с таким расчетом, чтобы их могли изготавливать заранее, независимо от места использования. Он построил ряд, приняв знаменатель прогрессии, обеспечивающий десятикратное увеличение каждого пятого члена ряда:

откуда:

В результате получается следующий ряд:

d - 1.58d – 2.51d – 3.98d – 6.31d – 10d - …

Значения этого ряда были заменены округленными величинами, удобными на практике:

1 – 1.6 – 2.5 – 4.0 – 6.3 – 10 - …

Данный ряд может быть продолжен в обоих направлениях.

В 1920 г. в Германии и в 1921 г. во Франции были утверждены первые стандарты, реализующие идею французского инженера. Его ряд получил обозначение «R5»

В 1953 г. международная организация по стандартизации (ИСО) утвердила параметрические стандарты. Кроме ряда R5 были утверждены ряды R₁₀, R₂₀ и R₄₀. Со знаменателями соответственно:

У нас в стране с 1985 г. действует ГОСТ 8032-84 Предпочтительные числа и ряды предпочтительных чисел.

Ряды предпочтительных чисел должны удовлетворять следующим требованиям:

1) представлять рациональную систему градаций, отвечающую требованиям производства и эксплуатации;

2) быть бесконечным как в сторону малых, так и в сторону больших значений, т.е. предусматривать неограниченное развитие параметров и размеров.

В ГОСТ 8032-84 установлено четыре основных ряда предпочтительных чисел и два дополнительных.

Таблица 1 – Общая характеристика предпочтительных чисел

Рассмотрим округленные значения предпочтительных чисел ряда R₄₀, который является самым применяемым в настоящее время.

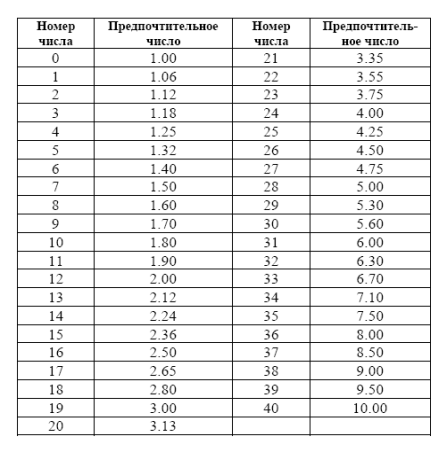
Таблица 2 – значения предпочтительных чисел ряда R₄₀

На примере ряда R40 рассмотрим основные свойства рядов предпочтительных чисел:

1. ГОСТ 8032 устанавливает стандартные значения предпочтительных чисел в диапазоне 0< d <∞ на основе фиксированных значений предпочтительных чисел, включенных в десятичный интервал 1< d ≤10. Все эти числа в ряде R₄₀ представлены в таблице 2.

Для перехода от предпочтительных чисел ряда R₄₀ в любой десятичный интервал необходимо умножить это число на 10^к, где к – целое положительное или отрицательное число.

Например:

1) при к=1 числа переходят в интервал 10< d ≤100;

2) при к=-1 числа переходят в интервал 0.1< d ≤1.

Например, стандартные предпочтительные числа образуются следующим образом:

1) 2.00*102=200;

2) 4.00*101=40;

3) 1.12*10-2=0.0112.

2. Номер ряда предпочтительных чисел (R₄₀ - R₁₆₀) указывает на количество чисел в десятичном интервале. Например, в ряде R₄₀ предпочтительных чисел, включая 10.00, будет 40.

3. Таблица ряда R₄₀ включает все основные ряды предпочтительных чисел R₅, R₁₀ и R₂₀.

Так, ряд R5 получается следующим образом:

1, 5 10, (5 10)2 , (5 10)3 , (5 10)4 и (5 10)5 .

После вычисления и округления получим числа ряда

R5: 1 – 1.6 – 2.5 – 4.0 – 6.3 – 10.

Аналогично образуются ряды R10, R20, R40, R80 и R160.