Безопасности полетов

Напомним (см. 3.2), что количественной характеристикой, оценивающей безопасность полетов, является уровень безопасности полетов (УБП). Под УБП подразумевается вероятность того, что в полете не возникнет катастрофической ситуации. Из определения УБП следует, что

(1)

где 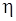– УБП; – вероятность возникновения в полете катастрофической ситуации.

Катастрофическая ситуация с большой степенью вероятности заканчивается катастрофой, поэтому можно принять, что

(2)

где n_к – количество катастроф; N – число полетов.

Самыми простыми статистическими критериями являются абсолютные, определяемые числом катастроф n_к и числом погибших . Однако эти простые критерии не дают возможности выполнять сравнительную оценку УБП по годам и по отдельным регионам. Поэтому для оценки УБП более рационально применять относительные статистические критерии. В этих показателях число неблагоприятных событий относится к объемному показателю: налету в часах и километрах, числу полетов, числу перевезенных пассажиров, объему перевозок.

Странами – членами ИКАО используются следующие относительные статистические критерии:

– число катастроф на 10⁸ км налета

;

где – налет, км;

– число катастроф на 10⁵ часов налета

;

где – налет, ч;

– число катастроф 10⁵ полетов

;

– число погибших на 1 миллион перевезенных пассажиров

– число погибших на 10⁸ пассажиро-километров

,

где 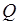– объем перевозок, пассажиро-километров.

Абсолютные критерии оценки УПБ – n_к и дают возможность оценить общие потери, но не могут быть применены для сравнительной оценки состояния БП. Относительный критерий K₁ прост для вычисления, однако не дает возможности провести объективную сравнительную оценку ВС, выполняющих полеты с различной скоростью и на различные расстояния.

Из анализа АП следует, что в горизонтальном полете происходит не более 16 % всех событий, остальные 84 % приходятся на взлет, набор высоты, снижение, заход на посадку и посадку. По времени все эти этапы занимают меньше времени, чем собственно горизонтальный полет. В связи с этим производить сравнение с помощью критериев БП K₁ и K₂ воздушных судов с различной продолжительностью и дальностью полетов нецелесообразно. По этим критериям самолеты на местных воздушных линиях с меньшей продолжительностью и дальностью полетов всегда будут несправедливо оцениваться как более опасные. Несправедливость такой оценки вытекает из того, что самолеты местных воздушных линий, выполняя по сравнению с дальними магистральными самолетами в 5...6 раз больше взлетов и посадок, чаще попадают в условия большей вероятности АП.

Критерий K₃ указывает на отношение числа катастроф к числу полетов и ближе всех подходит к зависимости (1), а, следовательно, и к оценке УБП (2).

Однако критерии K₁, K₂, K₃ не учитывают последствия катастроф, и, следовательно, с помощью этих критериев нельзя оценить размеры бедствий, приносимых катастрофами на воздушном транспорте. Согласно этим критериям, в число катастроф в качестве равноценных слагаемых входят и катастрофа небольшого ВС, в которой погиб один человек, и катастрофа многоместного воздушного лайнера, в которой погибли сотни людей.

Критерии K₄ и K₅ не учитывают показатель числа катастроф, но критерий K₅ удобно применять для сравнительной оценки различных видов транспорта. Результаты такой оценки показывают, что на авиационном и железнодорожном транспорте состояние безопасности практически одинаково, а на автомобильном транспорте в 10 раз хуже.

Для общей оценки БП целесообразно применение всех критериев. Однако при этом возникают затруднения в сравнительной оценке БП. Например, если за определенный период критерий K₅ уменьшился, а критерий K₃ увеличился, то это могло произойти не потому, что уменьшилась или увеличилась вероятность катастрофических ситуаций, а потому, что на воздушные линии вышли ВС с большей дальностью полетов.

Все рассмотренные критерии обладают тем недостатком, что кроме катастроф, они не учитывают таких авиационных событий, как аварии, поломки, а также предпосылки авиационных происшествий (ПАП), которые представляют собой потенциальную опасность. Кроме того, с помощью всех рассмотренных критериев невозможно сравнить состояние БП в отдельных авиационных предприятиях, если за наблюдаемый период в них отсутствовали катастрофы.

Критерий K₃ лучше всего раскрывает оценки УБП.

Все критерии рассчитываются применительно к годовому интервалу времени.

Авиационные катастрофы являются редкими событиями. Тем не менее, по статистическим данным можно определить тенденцию изменения критериев оценки БП. Для каждого из относительных показателей можно построить аппроксимирующие зависимости, которые позволят изучить динамику изменения показателей по времени.

Исходя из общей тенденции изменения критериев, аппроксимирующие функции выбирают в виде

(3)

где – аппроксимирующая функция; 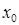и – искомые коэффициенты; – текущее время.

Зависимости (3) для проведения анализа иногда удобно записать в виде

, (4)

где – постоянная времени, характеризующая скорость изменения процесса.

При 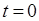зависимости (3) и (4) записывают в виде , а, следовательно, характеризует начальное значение функции. Для нахождения и выражение (3) логарифмируют, в результате чего получают

.

Для нахождения и составляют систему линейных алгебраических уравнений

(5)

где ; ; 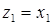; ; – значение критерия в i-й интервал времени (год).

Система (5) содержит два неизвестных. Решив такую систему по методу наименьших квадратов, находят значения и для всех критериев (табл. 5.1).

Чем больше значение , тем быстрее убывает значение соответствующего показателя (рис. 5.1–5.5).

0 10 20 год

Рис. 5.1. Изменение критерия K₁

0 10 20 год

Рис. 5.2. Изменение критерия K₂

0 10 20 год

Рис. 5.3. Изменение критерия K₃

0 10 20 год

Рис. 5.4. Изменение критерия K₄

0 10 20 год

Рис. 5.5. Изменение критерия K₅

Таблица 5.1