
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Твердая кристаллическая среда
Можно говорить о кристаллизации из твердой фазы, рекристаллизации, если первичная фаза: 1) аморфная, 2) кристаллическая мелкозернистая, 3) предварительно деформирована – имеет избыточную концентрацию ненасыщенных связей или 4) характеризуется полиморфизмом – способностью кристаллизоваться в нескольких модификациях.
Движущей силой кристаллизации в аморфных телах, рассматриваемых как переохлажденные жидкости, является избыточная свободная энергия по сравнению с телами с насыщенными дальними связями.
Движущая сила роста крупных кристаллов в мелкозернистой фазе черпается из избыточной свободной энергии границ кристаллитов. Граничная энергия может рассматриваться как своеобразное межфазное натяжение. Подобно тому как для малых частиц характерна высокая растворимость и высокое давление паров, так и малым зернам (кристаллитам) присуща большая поверхностная энергия, которая зависит от взаимной ориентации. Благоприятно ориентированные кристаллиты разрастаются за счет неблагоприятно ориентированных соседних кристаллитов. С укреплением зерна уменьшается натяжение, движущая сила ослабевает. Эти процессы коалесценции при нагреве (отжиге) ускоряются.
Если тело деформируют, то противодействующие усилия в деформированном теле, которые стремятся восстановить первоначальную форму (из-за межатомного притяжения), рождают напряжение. Образец, подвергнутый пластической деформации, становится сильно напряженным с большим запасом свободной энергии, служащей главным источником движущей силы рекристаллизации при деформированном отжиге.
Полиморфизм можно считать общим свойством кристаллических тел.
Всякая модификация должна иметь в фазовой диаграмме свою область существования, чтобы быть индивидуальной фазой. Модификации могут переходить друг в друга, изменение свойств при этом совершается скачком.
Превращение одной модификации в другую во многом аналогично переходу из твердого состояния в жидкое или обратно, но во втором случае упорядоченное расположение частиц в кристаллической решетке сменяется менее упорядоченным, а в первом - одна пространственная решетка заменяется другой.
При определенных условиях, когда разновидности могут существовать одновременно и даже в соприкосновении друг с другом, т.е. имеет место задержка в превращении, такое состояние одной неустойчивой фазы называется метастабильным.
Главный недостаток твердофазной кристаллизации – в трудности управления зародышеобразованием и следовательно, выращивания крупных монокристаллов.
Лекция 3.Поверхность кристалла.
Структура поверхности кристалла, от которой зависит поверхностная кинетика кристаллизации (механизм роста), определяется природой кристалла и условиями его роста, главным образом степенью отклонения от равновесия и температуры. Под структурой поверхности понимают концентрацию изломов и ступеней, конфигурацию и высоту ступеней, а также взаимное их расположение.
1) Поверхностная энергия кристалла и полярная диаграмма Вульфа
Поверхность кристалла характеризуется удельной свободной поверхностной энергией σ [дин / см = эрг / см2]. Это минимальная работа, необходимая для создания 1см2 границы кристалл – среда при абсолютном нуле температуры в условиях постоянного объема и давления.
В общем случае поверхностная энергия твердого тела, граничащая с жидкой фазой, меньше, чем на границе с газом, и зависит от примесей в кристалле и среде. Поверхностная энергия кристалла зависит от кристаллографической ориентации. Ее анизотропия – следствие решетчатого строения кристаллов.
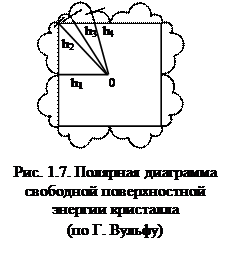 На рис. 1.7 представлена диаграмма Вульфа для кристалла Косселя (гомеополярного с простой кубической решеткой). Это графическое изображение зависимости поверхностной энергии кристалла от направления σ = σ (
На рис. 1.7 представлена диаграмма Вульфа для кристалла Косселя (гомеополярного с простой кубической решеткой). Это графическое изображение зависимости поверхностной энергии кристалла от направления σ = σ ( 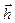 ), где
), где 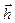 - вектор нормали к рассматриваемой границе раздела. Данное в полярных координатах главное сечение приблизительно сферической поверхности показывает зависимость свободной поверхностной энергии от направления. Расстояние от центра h пропорционально σ в данном направлении. Если в отдельных точках диаграммы провести плоскости, перпендикулярные соответствующие радиусам – векторам
- вектор нормали к рассматриваемой границе раздела. Данное в полярных координатах главное сечение приблизительно сферической поверхности показывает зависимость свободной поверхностной энергии от направления. Расстояние от центра h пропорционально σ в данном направлении. Если в отдельных точках диаграммы провести плоскости, перпендикулярные соответствующие радиусам – векторам 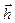 в этих точках, получим многогранник (на рис. 1.7 - куб), характеризующийся минимальной поверхностной энергией. Такая форма маленького кристалла является равновесной. Острые минимумы на полярной диаграмме соответствуют низкоиндексным граням. Грань со сложными индексами (hkl), отклоненная от ближайшей низкоиндексной н грани (100) на малый угол θ, может быть составлена участками плоскостей (100) и торцами незавершенных плоскостей (010). Ее поверхностная энергия равна:
в этих точках, получим многогранник (на рис. 1.7 - куб), характеризующийся минимальной поверхностной энергией. Такая форма маленького кристалла является равновесной. Острые минимумы на полярной диаграмме соответствуют низкоиндексным граням. Грань со сложными индексами (hkl), отклоненная от ближайшей низкоиндексной н грани (100) на малый угол θ, может быть составлена участками плоскостей (100) и торцами незавершенных плоскостей (010). Ее поверхностная энергия равна:
σ (θ) = σ(010) sin θ + σ(100) cos θ.
2) Классификация поверхностей кристалла
Различают равновесное состояние поверхности от того, которое имеет кристалл во время роста, при неравновесных условиях. Исследование равновесных поверхностных структур служит отправной точкой для изучения кинетики, и к тому же оно остается в силе и для достаточно малых отклонений от равновесия.
Рассмотрим сначала равновесную структуру поверхности идеально совершенного кристалла при абсолютном нуле температуры.
Атомная структура поверхности идеального кубического гомеополярного с примитивной решеткой кристалла, окруженного газом, схематически изображена на рис. 1.8, а. Идеализация предполагает кристалл свободным от внутренних дефектов, все одинаковые атомы представляются в виде плотноупакованных кубиков, у каждого из которых 6 ближайших соседей, соприкасающихся по граням куба. Вторую координационную сферу атома составляют 12 атомов, соприкасающихся с исходными по ребрам куба, и в третьей координационной сфере 8 соседей, имеющих с ним общие вершины. На рис. 1.8, а представлена модель атомно-гладкой грани (1) с незавершенным на ее поверхности слоем. Ряд атомов образует ступень (2), незавершенная ступень оканчивается изломом, положением у полукристалла (3).
Решетчатая структура кристалла – причина неодинаковой атомной структуры разных его граней: грани (100) отвечают две серии непараллельных цепей сильных химических связей, грани (110) – одна серия связей и грани (111) – ни одной. Понятие о ПЦС – периодических цепях связей – введено П. Гартманом и В. Пердоком. Грани, параллельные двум и более ПЦС, называются F-гранями, им соответствуют плоские сетки с большой ретикулярной плотностью. Это низкоиндексные плотноупакованные грани. Грани, характеризующиеся наличием одной серии цепей сильных связей, называются S-ступенчатыми. Наконец, К-ячеистые, не имеют ни одной цепи сильной связи, это грани атомно-шероховатые.
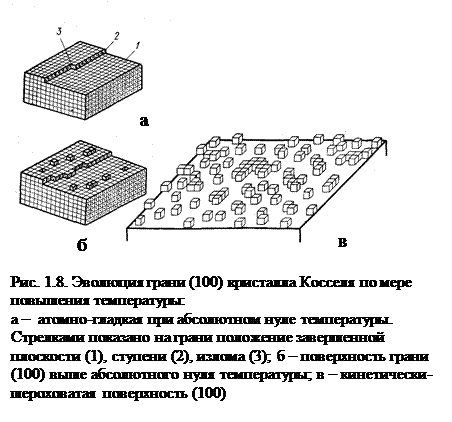 Иная картина поверхности плотноупакованной грани при температуре выше абсолютного нуля вблизи точки плавления (см. рис. 1.8, б). Вследствие термодинамических флуктуаций грань «портится» адсорбированными атомами (адатомами) и вакансиями и перестает быть гладкой. Вакансия – это узел решетки, в которой отсутствует атом или ион.
Иная картина поверхности плотноупакованной грани при температуре выше абсолютного нуля вблизи точки плавления (см. рис. 1.8, б). Вследствие термодинамических флуктуаций грань «портится» адсорбированными атомами (адатомами) и вакансиями и перестает быть гладкой. Вакансия – это узел решетки, в которой отсутствует атом или ион.
Небольшое отклонение от ориентации составляющих плотноупакованную грань приводит к ступенчатой поверхности. Сами края ступеней не могут быть гладкими и покрыты изломами. В. Бартон и др. показали, что в отличие от плотноупакованной грани ступени задолго до точки плавления испытывают «плавление», т.е. становятся шероховатыми с многочисленными изломами.
Предложена следующая классификация равновесных поверхностей кристалла: сингулярные, вицинальные и диффузные или несингулярные.
Сингулярные – это плотноупакованные грани, которым на полярной диаграмме Вульфа соответствуют острые минимумы.
Для вицинальных граней характерна ступенчатая структура, в которой довольно широкие участки плоскости с малыми индексами отделены друг от друга мономолекулярными «подъемами», или ступеньками.
Несингулярные, или атомно-шероховатые, представляют собой поверхности с другими ориентировками, отличными от ориентировки сингулярных.
Для «диффузной поверхности» характерны атомы, находящиеся в промежуточном состоянии между твердыми и жидкими. При этом жидкость обладает той же плотностью и тем же расположением атомов, что и кристалл, иная лишь энергия связи между частицами. Такая поверхность раздела противопоставляется шероховатой, где каждый атом в любом положении может быть определен как принадлежащий кристаллу или жидкости.
По мере отклонения системы от равновесия и увеличения температуры кристаллизации гладкая плотноупакованная грань может перейти в шероховатую (см. рис. 1.8, в). Шероховатость такого происхождения называется кинетической. Поскольку переходы от атомно-гладкого к шероховатому состоянию происходит при определенной температуре, они часто называются фазовыми переходами II рода.
Для кинетически-шероховатой грани на полярной диаграмме Вульфа острый минимум заменяется плавным из-за снижения анизотропии ее поверхностной энергии.
Плотноупакованная грань реального кристалла всегда более или менее богато скульптурована спиралями роста, обеспечивающими на грани ступени, и другими фигурами.
3) Адсорбция
Адсорбция обычно связана с наличием на поверхности кристаллического тела нескомпенсированного электрического поля.
Адсорбция имеет место, когда энергия взаимодействия между поверхностными частицами кристалла и контактирующей с ним среды превышает энергию взаимодействия частиц среды друг с другом. Согласно теории Фольмера, при соответствующем пересыщении частицы кристаллизуемого вещества, достигнув кристаллической поверхности, выделяют только часть своей энергии – скрытой теплоты, и поэтому отлагающиеся на твердой поверхности частицы, несмотря на сильное взаимодействие с поверхностью кристалла, сохраняют значительную свободу в отношении движения по поверхности кристалла, т.е. могут перемещаться по поверхности. В представлении М. Фольмера совокупность перемещающихся частиц и представляет собой адсорбционный слой, расположенный между фиксированной «неуспокоенной» поверхностью растущего кристалла и прилегающим слоем раствора.
Итак, моменту встраивания частицы в кристаллическую структуру предшествует акт объемной диффузии, проникновения частицы в адсорбционный слой. Частица, достигнув поверхности кристалла, либо закрепляется в данном месте «навсегда», либо в силу неистраченного остатка энергии мигрирует по поверхности (поверхностная диффузия) и закрепляется где-либо в другой позиции. Некоторый частицы, проблуждав по поверхности, отрываются от нее (десорбируются) и уходят обратно в среду. Очевидно, что концентрация кристаллизующихся частиц выше равновесной, количество адсорбирующихся частиц преобладает над количеством десорбирующихся.
Установившиеся процессы адсорбции динамически равновесны, т.е. частицы адсорбата на внешней поверхности адсорбента лишь временно закреплены и при данных условиях рано или поздно могут покинуть ее, освободив место для таких же или иных частиц.
Крайний случай адсорбции, когда посторонние частицы навсегда закрепляются на поверхности адсорбента, наблюдается в эпитаксии – ориентированном наращивании чужого вещества на кристаллической поверхности. Экспериментальными работами показано, что эпитаксия определяется двумерным подобием кристаллических решеток в составляющих сетках. Однако этот признак нельзя считать универсальным.
От эпитаксии можно формально перейти к изоморфизму, ели представить, что одно вещество закономерно отлагается на всех гранях другого. Изоморфная примесь будет адсорбироваться кристаллом практически в той же степени, что и собственные частицы кристалла. Иначе говоря, изоморфная примесь слабо влияет на скорости роста граней.
Т.о., эпитаксия и изоморфизм могут рассматриваться и как частные случаи общего явления адсорбции.
Лекция 4.Образование зародышей.
Под зародышеобразованием понимают локализованное возникновение небольшого объема (радиус от единицы до десятков ангстрем) новой фазы в маточной среде. Этот путь фазовых превращений противопоставляется другому, когда малое превращение распространено по большому объему (массовая кристаллизация). Вопрос о зародышеобразовании тесно связан с проблемой существования метастабильной области и ее протяженности.
Различают гомогенноезародышеобразование (спонтанное, самопроизвольное) и гетерогенное (на поверхностях раздела фаз).
1) Гомогенное зародышеобразование
Как известно, рост кристалла (увеличение его объема) сопровождается уменьшением свободной энергии кристаллизующейся системы ( 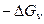 ), а возникновение трехмерного зародыша (поверхностей раздела кристалл - среда), напротив, требует затраты определенной энергии (
), а возникновение трехмерного зародыша (поверхностей раздела кристалл - среда), напротив, требует затраты определенной энергии ( 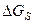 ) и поэтому всегда сопровождается увеличением свободной энергии системы на величину
) и поэтому всегда сопровождается увеличением свободной энергии системы на величину 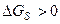 .
.
Т.о. общее изменение свободной энергии системы  (изменение термодинамического потенциала
(изменение термодинамического потенциала 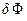 ) при образовании в ней изотропного трехмерного зародыша складывается из его объемной энергии
) при образовании в ней изотропного трехмерного зародыша складывается из его объемной энергии 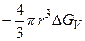 и поверхностной свободной энергии
и поверхностной свободной энергии  , где
, где  - радиус зародыша:
- радиус зародыша:
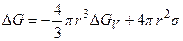 или
или 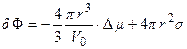 (1.22),
(1.22),
где  - число частиц, из которых состоит зародыш,
- число частиц, из которых состоит зародыш, 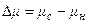 .
.
Значения двух слагаемых 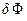 - работы образования кристаллического агрегата по-разному зависит от r - размера агрегата (рис. 1.9): знаки разные, в одном случае (2) - кубическая, в другом (1) – квадратичная зависимость. Поэтому зависимость
- работы образования кристаллического агрегата по-разному зависит от r - размера агрегата (рис. 1.9): знаки разные, в одном случае (2) - кубическая, в другом (1) – квадратичная зависимость. Поэтому зависимость 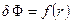 носит сложный (3), не монотонный характер.
носит сложный (3), не монотонный характер.
 Кристаллический агрегат с радиусом r < rk склонен к растворению. Зародыши критического размера rk могут с равной вероятностью расти и растворяться. Жизнеспособными оказываются те зародыши, радиус которых больше критического r > rk , рост их будет сопровождаться уменьшением термодинамического потенциала, т.е. будет термодинамически выгодным.
Кристаллический агрегат с радиусом r < rk склонен к растворению. Зародыши критического размера rk могут с равной вероятностью расти и растворяться. Жизнеспособными оказываются те зародыши, радиус которых больше критического r > rk , рост их будет сопровождаться уменьшением термодинамического потенциала, т.е. будет термодинамически выгодным.
Согласно теории Фольмера энергия, необходимая для самопроизвольного возникновения жизнеспособного зародыша изыскивается системой за счет флуктуаций энергии. Если бы не было этих флуктуаций, метастабильная система при отсутствии внешних воздействий существовала бы неопределенно долгое время без каких-либо признаков кристаллизации.
Как функция вероятностная, энергия изолированной метастабильной системы испытывает непрерывный ряд малых беспорядочных изменений – флуктуаций, оставаясь тем самым все время меньшей максимального значения, но близкой к нему. Соответственно этому параметры системы (концентрация, температура, давление и т.д.) в отдельных ее частях не остаются постоянными, а колеблются около некоторых средних значений, отвечающих максимуму энтропии системы. Вероятность возникновения зародыша W в значительной степени зависит от 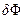 :
:
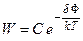 , (1.23)
, (1.23)
где С – предъэкпоненциальный множитель, который зависит от продолжительности жизни зародыша, но который нельзя вычислить в термодинамике. Нужно помнить, что продолжительность жизни зародыша, возникшего в результате флуктуации, но не достигшего критического размера, мала. Возникнув, он в большинстве случаев вскоре распадается. Для зародышей, которые не распадаются, удается выразить зависимость между энергетическим фактором и вероятностью их образования на основе молекулярно-кинетических представлений, изложенных ниже.
Зародыш критического размера обладает максимальным значением 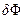 , при дальнейшем росте зародыша происходит непрерывное уменьшение его свободной энергии. Критический размер зародыша rk находим из условия:
, при дальнейшем росте зародыша происходит непрерывное уменьшение его свободной энергии. Критический размер зародыша rk находим из условия:
 (1.24),
(1.24),
откуда 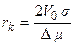 .
.
Из уравнения (1.24) получаем условие равновесия сферического кристалла со средой:
 .
.
Подставляя значение (1.24) в формулу (1.22), определяем работу образования критического зародыша 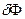 (высоту барьера зародышеобразования):
(высоту барьера зародышеобразования):
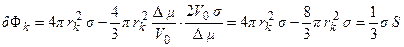 , (1.25, а)
, (1.25, а)
где 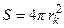 - величина поверхности зародыша. Эта работа необходима для изотермического обратимого образования равновесной капли из пересыщенного пара и равна одной трети свободной поверхностной энергии капли.
- величина поверхности зародыша. Эта работа необходима для изотермического обратимого образования равновесной капли из пересыщенного пара и равна одной трети свободной поверхностной энергии капли.
Аналогичные рассуждения применимы к образованию кристаллической фазы в пересыщенном растворе или переохлажденном расплаве. Гиббс показал, что образующийся кристаллический зародыш для сохранения равновесия с жидкостью приобретает форму, отвечающую минимальному значению его свободной поверхностной энергии при постоянном объеме,
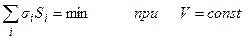 , (1.25, б)
, (1.25, б)
где 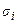 - поверхностная энергия i-той грани, а Si– ее площадь. Суммирование распространяется на все грани.
- поверхностная энергия i-той грани, а Si– ее площадь. Суммирование распространяется на все грани.
Работа А образования кристаллического зародыша равна:
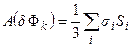 (1.26)
(1.26)
Если значения rk (1.24) и 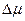 подставить в уравнение (1.22), то получим высоту активационного барьера для образования зародыша в зависимости от степени пересыщения (переохлаждения) γ:
подставить в уравнение (1.22), то получим высоту активационного барьера для образования зародыша в зависимости от степени пересыщения (переохлаждения) γ:
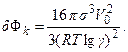 (1.27)
(1.27)
Уравнение (1.27) дает конкретный физический смысл понятию о границе метастабильности.
Энергетический барьер при зарождении кристаллов находится в кубической зависимости от поверхностной энергии и потому при зарождении в газовых фазах он высок, в растворах он значительно ниже и еще ниже в расплавах. В фазовых переходах второго рода поверхностная энергия равна нулю, следовательно, и 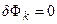 .
.
Уравнение (1.27) показывает, что в насыщенном ( 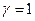 ) растворе невозможна самопроизвольная кристаллизация, так как при
) растворе невозможна самопроизвольная кристаллизация, так как при 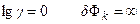 , т.е. энергия образования зародышей бесконечно велика.
, т.е. энергия образования зародышей бесконечно велика.
2) Гетерогенное зародышеобразование
Впервые Фольмер указал, что во всех процессах образования новой фазы большую роль играет твердая стенка, а также любая поверхность раздела (гетерогенное зарождение), которые облегчают образование устойчивых зародышей.
Пусть осевшая на стенке капля с радиусом кривизны r находится в равновесии со своим паром (рис. 1.10).Условием равновесия сил поверхностного натяжения будет:
 (1.28)
(1.28)
где 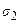 - поверхностное натяжение твердой стенки на границе с паром;
- поверхностное натяжение твердой стенки на границе с паром; 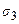 - поверхностное натяжение твердой стенки на границе с жидкостью;
- поверхностное натяжение твердой стенки на границе с жидкостью; 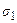 - поверхностное натяжение капли;
- поверхностное натяжение капли;  - краевой угол.
- краевой угол.
По формуле Гиббса (1.26), работа  образования равновесной капли на твердой стенке равна:
образования равновесной капли на твердой стенке равна:
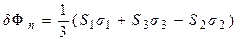 ,
,
где S1 - поверхность сегмента капли; S2 = S3 – площадь основания сегмента капли. Поверхность шарового сегмента  , где r – радиус шара; h – высота сегмента. Из рис. 1.10 находим:
, где r – радиус шара; h – высота сегмента. Из рис. 1.10 находим:
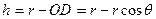 , следовательно,
, следовательно, 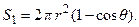
 Площадь основания капли:
Площадь основания капли:
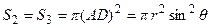 ,
,
откуда 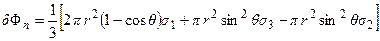
или из формулы (1.28)  (1.29)
(1.29)
Сравнивая выражение (1.29) с (1.25, а), видим, что энергия образования зародыша на стенке всегда меньше энергии его образования в свободном пространстве. Первая настолько сильно зависит от значения краевого угла  , что при
, что при 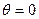 ,она равна нулю, т.е. на абсолютно смачиваемой поверхности конденсация паров начинается при самом незначительном пересыщении. Энергия достигает максимального значения при
,она равна нулю, т.е. на абсолютно смачиваемой поверхности конденсация паров начинается при самом незначительном пересыщении. Энергия достигает максимального значения при 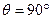 , а при
, а при 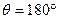 приравнивается к энергии гомогенного зародышеобразования (1.25, а).
приравнивается к энергии гомогенного зародышеобразования (1.25, а).
Необходимо учитывать, что работа  определяется еще и физическим состоянием поверхности. Если на поверхности есть узкие трещины, то работа может сделаться даже отрицательной, т.е. конденсация будет происходить уже в ненасыщенном паре.
определяется еще и физическим состоянием поверхности. Если на поверхности есть узкие трещины, то работа может сделаться даже отрицательной, т.е. конденсация будет происходить уже в ненасыщенном паре.
Характер зависимости 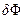 от r такой же, как и при гомогенном зарождении, но максимум на кривой
от r такой же, как и при гомогенном зарождении, но максимум на кривой 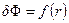 ниже.
ниже.
Подстановкой в уравнение (1.29) значения 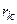 можно выразить работу образования критического зародыша через пересыщение для изотропного случая на подложке, имеющей форму диска:
можно выразить работу образования критического зародыша через пересыщение для изотропного случая на подложке, имеющей форму диска:
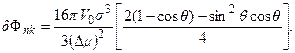 (1.30)
(1.30)
 Для анизотропного варианта Фольмер ввел понятие о двумерном зародыше на поверхности гладкой грани, растущей за счет этих зародышей. Такой зародыш на гладкой грани представляет собой как бы остров плоской мономолекулярной сетки (рис. 1.11), который при данном пересыщении (переохлаждении) исходной фазы находится в состоянии равновесия. Равновесная форма определяется условием Гиббса (1.25, б), записанным для двумерного варианта:
Для анизотропного варианта Фольмер ввел понятие о двумерном зародыше на поверхности гладкой грани, растущей за счет этих зародышей. Такой зародыш на гладкой грани представляет собой как бы остров плоской мономолекулярной сетки (рис. 1.11), который при данном пересыщении (переохлаждении) исходной фазы находится в состоянии равновесия. Равновесная форма определяется условием Гиббса (1.25, б), записанным для двумерного варианта:
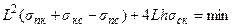 (1.31)
(1.31)
при 
В другом виде условие равновесия такого зародыша известно как правило Вульфа:
 (1.32)
(1.32)
Здесь 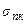 - поверхностная энергия границы подложка – кристалл;
- поверхностная энергия границы подложка – кристалл; 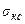 - поверхностная энергия границы
- поверхностная энергия границы
кристалл – среда; 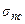 - поверхностная энергия границы подложка – среда.
- поверхностная энергия границы подложка – среда.
Если смачивание хорошее, т.е. 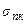 +
+ 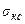 мала, зародыш уплощается, имеет малую высоту h. Если смачивание плохое, h увеличивается, кристалл вытягивается в столбик. На собственной подложке
мала, зародыш уплощается, имеет малую высоту h. Если смачивание плохое, h увеличивается, кристалл вытягивается в столбик. На собственной подложке 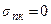 , а
, а 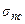 =
= 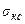 , тогда
, тогда 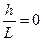 означает полное растекание. Реально же h не меньше межатомного расстояния. В Фольмеровском двумерном зародыше h составляет межатомное расстояние а.
означает полное растекание. Реально же h не меньше межатомного расстояния. В Фольмеровском двумерном зародыше h составляет межатомное расстояние а.
Работа образования двумерного зародыша на гладкой грани собственного кристалла и величина критического зародыша определяются формулами:
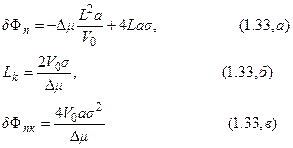
где 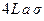 - краевая энергия зародыша.
- краевая энергия зародыша.
Работа гетерогенного образования зародышей меньше работы гомогенного зародышеобразования на величину, зависящую от смачиваемости подложки и от кристаллохимического соответствия сопрягающихся структур.
3) Эпитаксия
Частным случаем гетерогенного зародышеобразования представляется автоэпитаксия – простейшее проявление закономерного срастания кристаллов, ориентированное наращивание вещества на кристаллической поверхности. В некотором смысле все кристаллы образуются в результате эпитаксиального роста: каждый осаждающий слой имеет ту же ориентировку, что и слой, лежащий под ним. Однако термин «эпитаксия», впервые введенный Руайе, обычно используется для описания ориентированной кристаллизации на инородных подложках.
Различают автоэпитаксию, гетероэпитаксию и хемоэпитаксию.
Автоэпитаксия – ориентированное наращивание кристаллического вещества, отличающегося от подложки только примесным составом (Ge + Ag на Ge).
Гетероэпитаксия – ориентированное нарастание на кристалле инородного кристаллического вещества без участия химических реакций. Гетероэпитаксия возможна в случае полностью растворимых веществ, в системах с образованием эвтектики и, наконец, в системах с непрерывным рядом твердых растворов. Последний случай особенно благоприятен для срастания двух фаз.
Хемоэпитаксия – ориентированное нарастание при химическом взаимодействии подложки с нарастающим веществом. Примером служит образование пленок окислов на поверхности металлов.
В ранних исследованиях эпитаксии большое внимание уделялось размерному соответствию параметров решеток в плоскости срастания. Согласно правилу Руайе – Фриделя ориентация возможна лишь тогда, когда между срастающимися сетками решетки существует геометрическое и размерное соответствие. Ориентированное срастание требует, чтобы разница в параметрах сеток срастающихся соединений не превышала 10 – 15 %. Однако было отмечено немалое число случаев эпитаксии и при значительно большей разнице. Обычно обращает внимание то, что при эпитаксии срастание осуществляется на кристаллических плоскостях с низкими индексами.
По П. Д. Данкову, на поверхности подложки происходят два различных кристаллизационных процесса: образование двумерного зародыша под влиянием направляющих сил поверхности подложки и одновременно образование трехмерного зародыша, для которого не обязательна определенная ориентация по отношению к подложке. Эпитаксия связана с образованием двумерного зародыша. Между решетками подложки и кристаллизующегося вещества обычно не существует полного соответствия, следовательно, двумерный зародыш несколько деформируется. Если эта деформация достаточно велика, энергетически более выгодным может оказаться образование трехмерного зародыша, и в этих случаях эпитаксия не наблюдается. Т.о., основное условие эпитаксии записывается в виде:
А2D = A20 + ED ≤ A3, (1.34)
где А2D - работа образования деформированного двумерного зародыша; A20- работа образования недеформированного двумерного зародыша тех же размеров; А3 – работа образования трехмерного зародыша; ЕD – работа деформации. Так как A20 << A3,
А2D ≥ ED.
Сейчас в отношении гетерогенного зародышеобразования имеются три основных точки зрения: 1) оно происходит статистически из двумерного газа; 2) оно протекает только на активных центрах, преимущественно на точечных дефектах, и 3) компромиссная точка зрения, согласно которой при малых пересыщениях зародышеобразование происходит избирательно, а при больших – статистически.
Первой точки зрения придерживался Л. С. Палатник, работы которого по изучению механизма конденсации металлического пара в вакууме указывают на возможность образования кристаллической фазы либо непосредственно из пара (по схеме п  к), либо через жидкую фазу (по схеме п
к), либо через жидкую фазу (по схеме п  ж
ж  к). Начальную стадию образования конденсата на нейтральной подложке можно представлять как «двумерную кристаллизацию» или сжижение «двумерного металлического пара», образующегося на подложке. Механизм конденсации в вакууме определяется температурой подложки и плотностью газового потока.
к). Начальную стадию образования конденсата на нейтральной подложке можно представлять как «двумерную кристаллизацию» или сжижение «двумерного металлического пара», образующегося на подложке. Механизм конденсации в вакууме определяется температурой подложки и плотностью газового потока.
Работы Г. И. Дистлера дают материал в пользу второй точки зрения, согласно которой кристаллизация представляет собой репликационный процесс, запрограммированный в электрически активной структуре поверхности кристалла – подложки. Подложки действуют в качестве электрически активных матриц. Активная структура кристаллов слагается из различных структурных дефектов, главную роль среди которых играют точечные.
Группа ученых, начиная с И. Странского и Р. Кашиева, П. Данкова и Г. Близнакова придерживается мнения, что принципиально возможно два механизма образования эпитаксиальных пленок: непрерывный рост и спонтанная кристаллизация. В первом случае процесс роста осуществляется за счет присоединения атомов у активных центров подложки: изломов, ступенек, недостроенных атомных плоскостей, дислокаций, скоплений дефектов и т.п. Желательно, чтобы скорость роста слоя вдоль поверхности была больше скорости возникновения нового слоя.
Спонтанное образование зародышей облегчено, когда пересыщение превышает критическое значение, в некоторый момент могут образоваться зародыши приблизительно одинакового размера, и до определенного момента число их будет увеличиваться без существенного изменения размеров. По мере осаждения трехмерные зародыши разрастаются вплоть до образования сплошной пленки. Поскольку маловероятно, чтобы расстояния между кристаллами оказались величинами, в точности кратными периодам их решетки, то при встрече растущих кристаллов образуются дефекты. Часто трудно судить, является ли тонкая пленка в действительности сплошной или нет. Структуру обычно определяют с помощью малоугловой дифракции электронов.
Подложка должна быть монокристальной с гладкой поверхностью. Если на поверхности подложки высота ступеньки велика, то соответственно крупные ступеньки образуются и в пленках. В качестве подложек часто используют поверхности скола каменной соли и слюды. Нередко выгодны металлические подложки, поскольку осажденные на них пленки становятся сплошными при меньших толщинах и содержат меньше дефектов, чем в пленках, выращенных на подложках – ионных кристаллах.
Существенный фактор при эпитаксиальном росте – температура подложки, которая влияет на критический размер и скорость образования, а также на подвижность адсорбированных атомов. Предполагается определенная «температура ориентации», ниже и выше которой ориентация затруднена. При «температуре ориентации» скорость образования зародышей мала, адсорбированные частицы сохраняют такую подвижность на поверхности подложек, которая способствует занятию наиболее благоприятных с энергетической точки зрения положений на подложке. Плена растет из меньшего числа зародышей с небольшим числом дефектов, возникающих при соприкосновении зародышей.
Эпитаксиальная температура зависит как от свойств подложки, так и от скорости осаждения. По мере увеличения скорости осаждения пленки становятся менее совершенными, что связано и с более значительной их разориентировкой.
В общем случае действует правило: структурное совершенство тем выше, чем меньше исходные концентрации веществ и чем выше температура подложек.
Экспериментально показано, что ориентация происходит в две стадии: в стадию роста и коалесценции (слияния островков в одну пленочку). Коалесценция вступает в действие уже при заметных расстояниях между частицами (~ 100 – 1000 Å).
Можно различить эпитаксию I и II рода.
Эпитаксия I рода – текстурированные слои, которые отвечают условию:
(h1 k1 l1) || (h2 k2 l2). Это кристаллизация на подложках с одномерной ориентацией, где единые кристаллы могут быть любым образом повернуты относительно друг друга и соответственно подложка может быть бесструктурной, аморфной.
В эпитаксии I рода предполагается постепенный переход неориентированного первого слоя новой фазы в ориентированные последующие слои.
Эпитаксия II рода – ориентация двух направлений относительно симметрии подложки.
4) Факторы, влияющие на зарождение кристаллов
Из уравнения (1.24) видно, что важнейшим фактором в зарождении кристаллов остается движущая сила кристаллизации; те же факторы, которые способствуют протяженности метастабильной области, так или иначе препятствуют зарождению кристаллов.
На зарождение кристаллов оказывают влияние соприкасающиеся с жидкостью поверхности твердых тел, в частности стенка сосуда. Отдельные участки неоднородной поверхности обладают по отношению к образованию новой фазы различной активностью, которая определяется как физико-химической природой участка, так и его геометрической формой и размерами. Зарождению кристаллов способствуют и такие дефекты на поверхностях твердых тел, как трещины и каналы почти молекулярного размера.
На зарождение центров кристаллизации влияет число «обработок», предшествующих опыту и заключающихся в том, что выращенные из раствора кристаллы растворяются в свежей порции того же растворителя. Из полученного раствора вновь выращиваются кристаллы, которые тут же подвергаются растворению и т.д. С другой стороны, с ускорением перемешивания выравнивается концентрация и температура системы и снижается вероятность флуктуационного образования зародышей. При увеличении числа чередующихся операций скорость зарождения кристаллов падает. Обработку нужно рассматривать как способ самоочистки вещества от нагреваемых примесей, часть которых всегда оттесняется поверхностью растущего кристалла.
Перемешивание ускоряет возникновение зародышей, при этом его влияние носит сложный характер. Скорость диффузионного подвода кристаллизующего вещества к образующемуся зародышу увеличивается одновременно с дополнительным отщеплением твердых частиц с поверхностей, контактирующих с раствором.
Перемешивание и другие внешние воздействия (направленный теплоотвод, воздействие ультразвуковых, электрических и других полей) создают также флуктуации плотности и энергии и тем самым способствуют появлению жизнеспособных зародышей.
При воздействии электрических и магнитных полей число возникающих центров кристаллизации находятся в прямой зависимости от напряженности поля. В этих полях молекулы вещества (переохлажденной жидкости), ориентируясь в одном направлении, создают анизотропную среду, во многом аналогичную кристаллической. Воздействие магнитного поля уменьшает дефектность структуры быстро выращиваемых кристаллов из водных растворов.
Незначительные высокочастотные колебания воздействуют на кристаллизацию. Ультразвуковое поле настолько ускоряет процесс кристаллизации, что в результате получаются слитки с дендритной структурой. Механизм действия ультразвука в ультразвуковом поле сводится к происходящему на границе раздела двух фаз отщеплению мельчайших кристаллов, совершающих колебательные движения и увеличивающихся в размерах. Такое «почкование» способствует лавинообразному разрастанию процесса зарождения. Срастаясь с кристаллом, зародыши образуют поликристаллический слиток. Скорость этого процесса зависит от интенсивности ультразвукового поля.
Велика роль ионизирующего излучения, например γ-излучения радия. Его эффект сводится к увеличению числа центров кристаллизации. За счет поляризующего действия возникающих ионов на нейтральные молекулы первые становятся центрами окружения как ионов противоположного знака, так и этих молекул, и вокруг образующейся достаточно устойчивой группы начинается рост кристаллов.
Тема 2: Теории роста кристаллов.
В настоящее время наиболее развиты теории послойного роста кристаллов (молекулярно-кинетические и дислокационная) и теории нормального, или молекулярно-шероховатого, роста кристаллов из расплавов, и признан кристаллохимический подход в объяснении процессов кристаллизации.
Лекция 1.Механизмы роста кристаллов.
1) Механизм роста кристаллов двумерными зародышами.
Согласно теории Косселя кристалл растет посредством повторимого хода, путем встраивания частиц в структуру только в привилегированных местах роста, которыми служат изломы (положения у полукристалла). Повторимые ходы частиц, увеличивая объем кристалла, не изменяют его поверхности, следовательно, не изменяют и поверхностной энергии.
С другой стороны, источниками изломов на плотноупакованной гладкой (сингулярной) грани служат ступени. Последние благодаря высокой плотности изломов представляют собой своего рода стоки для адсорбированных одиночных атомов. В условиях роста ступенчатые участки (на вицинальных гранях) выклиниваются, оставляя позади себя сингулярную поверхность, дальнейший рост которой возможен при появлении новых источников ступеней.
Этими источниками ступеней служат двумерные зародыши, дислокации, места соприкосновения между кристаллом и его контейнером, границы зерен между двумя соприкасающимися кристаллами различной ориентации, инородные макроскопические частицы, двойники и т. д.
Энергии ступеней разной генерации и частоты присоединения в них (ступенях) неодинаковы, поэтому выделяют механизм роста сингулярной грани двумерными зародышами и дислокационный механизм.
Несингулярная грань растет нормальным механизмом.Механизм нормального роста определяется непрерывным присоединением частиц по всей шероховатой поверхности, равномерно покрытой изломами, количество которых не лимитирует скорости кристаллизации.
При больших  в метастабильной области рост кристалла может идти за счет присоединения уже имеющихся в среде трехмерных агрегатов частиц («зародышей», «ассоциатов»). С увеличением движущей силы кристаллизации доля, вносимая в скорость роста этим механизмом, должна увеличиваться.
в метастабильной области рост кристалла может идти за счет присоединения уже имеющихся в среде трехмерных агрегатов частиц («зародышей», «ассоциатов»). С увеличением движущей силы кристаллизации доля, вносимая в скорость роста этим механизмом, должна увеличиваться.
Покажем, что кинетика кристаллизации бездефектной сингулярной грани при небольших отклонениях системы от равновесия  лимитируется скоростью образования двумерного зародыша In . Согласно расчетам (Бартон и др., 1959) вероятность (скорость) образования двумерного зародыша мала вплоть до относительного пересыщения β в несколько десятков процентов. Тангенциальное же разрастание его Λ происходит с большой скоростью.
лимитируется скоростью образования двумерного зародыша In . Согласно расчетам (Бартон и др., 1959) вероятность (скорость) образования двумерного зародыша мала вплоть до относительного пересыщения β в несколько десятков процентов. Тангенциальное же разрастание его Λ происходит с большой скоростью.
Скорость движения одиночной прямолинейной ступени «элементарной»(соответствующей в кристалле Косселя ребру элементарной ячейки) высоты. Ступени, растущие на поверхности кристалла, имеют фронт, изрезанный изломами. Адсорбированные на грани частицы образуют адсорбционный слой, находящийся в равновесии с изломами и окружающей кристалл средой. Если равновесие нарушается, то в местах изломов, переход частиц в твердую фазу ведет к возникновению на поверхности плоских потоков. Расход вещества в адсорбционном слое пополняется за счет поступления новых молекул из окружающей среды. Таким образом, непосредственно конденсация происходит на боковых участках ступеней. Процесс роста ступени из газовой фазы определяется движением частиц по схеме: пар  адсорбционный слой
адсорбционный слой 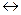 ступень, вдоль ступени
ступень, вдоль ступени 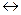 излом.
излом.
Вероятность прямого попадания атома из пара в ступень или ее излом мала, так как площадь торца ступени составляет всего лишь ~ 0,01% от площади вицинальной грани. Плотность же изломов велика, диффузия атомов вдоль ступени к излому не может быть лимитирующей стадией. Равновесие адсорбционный слой - ступень достигается мгновенно.
Общий поток атомов jV за счет объемной диффузии из пара в адсорбционный слой равен:
 (2.1)
(2.1)
где αк - коэффициент конденсации (аккомодации) для перехода пар  адсорбционный слой, меньший единицы; коэффициент акпредставляет собой отношение числа частиц, «застрявших» в адсорбционном слое к числу частиц, столкнувшихся с ним, так как часть их отражается поверхностью этого слоя. Пренебрегая движением ступени и учитывая большую скорость обмена адатомов с изломами, можно jV выразить через концентрацию адатомов в адсорбционном слое, достигшего стационарного состояния:
адсорбционный слой, меньший единицы; коэффициент акпредставляет собой отношение числа частиц, «застрявших» в адсорбционном слое к числу частиц, столкнувшихся с ним, так как часть их отражается поверхностью этого слоя. Пренебрегая движением ступени и учитывая большую скорость обмена адатомов с изломами, можно jV выразить через концентрацию адатомов в адсорбционном слое, достигшего стационарного состояния: 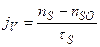 ,
,
где 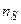 - действительная концентрация адатомов на поверхности вдали от ступени при условии равновесия с газовой фазой;
- действительная концентрация адатомов на поверхности вдали от ступени при условии равновесия с газовой фазой; 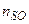 - равновесная поверхностная концентрация адатомов, равная концентрации у ступени; τS - время жизни адатома на поверхности до ухода его в пар. Величина
- равновесная поверхностная концентрация адатомов, равная концентрации у ступени; τS - время жизни адатома на поверхности до ухода его в пар. Величина 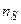 определяется
определяется 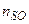 и степенью пересыщения γ:
и степенью пересыщения γ:
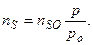 (2.2)
(2.2)
Диффузионный закон Фика (для одномерного диффузионного потока вдоль оси у, перпендикулярной к ступени) записывается в виде:
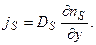 (2.3)
(2.3)
Наименьшая длина стока (у) частиц, прилипших к плоской поверхности, к ступени определяется длиной их свободного пробега XS. Заменяя в формуле (2.3)  потоком на ступень (nS - nSO), y - XS получим выражение скорости движения прямолинейной ступени Λ∞:
потоком на ступень (nS - nSO), y - XS получим выражение скорости движения прямолинейной ступени Λ∞:
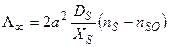 , (2.4)
, (2.4)
здесь множитель 2 определяется потоком частиц к ступени с двух сторон, а2 — площадь, занимаемая одной частицей, 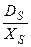 - скорость поверхностной диффузии.
- скорость поверхностной диффузии.
Для того чтобы выразить Λ∞ через пересыщение, вспомним, что  (из уравнения Эйнштейна), а также
(из уравнения Эйнштейна), а также  , (2.2) и подставим их в формулу (2.4). Тогда
, (2.2) и подставим их в формулу (2.4). Тогда
 (2.5)
(2.5)
где W - полная энергия испарения адатома, равная 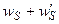 .
.
Физический смысл уравнения (2.5) состоит в следующем. Молекулы, ударившись о поверхность кристалла в «диффузионной зоне» шириной в 2XS, будут адсорбироваться на движущейся ступени с большим числом мест обмена (изломов). Скорость, с которой движется край слоя, пропорциональна относительному пересыщению 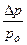 . По достижении слоем края кристалла его «творческая» функция прекращается, он образует завершенную поверхность. Дальнейший рост возможен только при образовании новой ступени. Сравнение двух скоростей In и Λ говорит в пользу второй, находящейся не в экспоненциальной зависимости от
. По достижении слоем края кристалла его «творческая» функция прекращается, он образует завершенную поверхность. Дальнейший рост возможен только при образовании новой ступени. Сравнение двух скоростей In и Λ говорит в пользу второй, находящейся не в экспоненциальной зависимости от 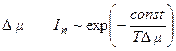 , а в линейной Λ ~ Δμ. Медленная стадия роста сингулярной грани, стадия образования на ней двумерного зародыша (ступени) и будет лимитирующей.
, а в линейной Λ ~ Δμ. Медленная стадия роста сингулярной грани, стадия образования на ней двумерного зародыша (ступени) и будет лимитирующей.
И. Н. Странский и Р. Каишев (1939) указывают на следующую зависимость нормальной скорости роста грани V(λ) от переохлаждения ΔТ:
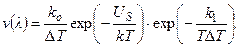 (2.6)
(2.6)
где k0 - множитель, слабо зависящий от температуры; Us -энергия активации, требуемая для присоединения новых атомных рядов к периферии двумерного зародыша; k1 — константа, связанная с существованием энергетического порога для образования двумерного зародыша на грани растущего кристалла. В этой формуле предполагается, что каждый образующийся зародыш разрастается на всю плоскость. Если одновременно образуется несколько зародышей на грани, то скорость роста грани будет меньше. Такие и более сложные ситуации будут рассмотрены позднее.
 График зависимости скорости роста v(λ) от пересыщения (рис. 2.1) подтвержден экспериментально на примере роста кристалла из пара. Можно видеть, что существует некоторое критическое пересыщение βk, необходимое для образования двумерных зародышей. При β > βk скорость роста сингулярной грани не лимитируется скоростью образования двумерных зародышей и линейно зависит от пересыщения. В растворах подобные зависимости однозначно определить трудно из-за адсорбированной «шубы» из растворителя. Признаком двумерного зародышеобразования может служить образование слоев у ребер и вершин. Однако такое образование часто происходит благодаря особенностям диффузионного поля около кристалла.
График зависимости скорости роста v(λ) от пересыщения (рис. 2.1) подтвержден экспериментально на примере роста кристалла из пара. Можно видеть, что существует некоторое критическое пересыщение βk, необходимое для образования двумерных зародышей. При β > βk скорость роста сингулярной грани не лимитируется скоростью образования двумерных зародышей и линейно зависит от пересыщения. В растворах подобные зависимости однозначно определить трудно из-за адсорбированной «шубы» из растворителя. Признаком двумерного зародышеобразования может служить образование слоев у ребер и вершин. Однако такое образование часто происходит благодаря особенностям диффузионного поля около кристалла.
Р. Каишевым (1966) достаточно убедительно доказано двумерное зарождение и распространение слоев при электрокристаллизации на совершенных гранях кристаллов серебра. При подаче тока на торец кристалла Ag, растущего из раствора азотнокислого серебра в форме капилляра, автор добивался получения прерывистого прохождения тока в виде отдельных импульсов. Эта прерывистость определяется прерывистым характером кристаллизации серебра, во время которой и проходил ток. Количество электричества, протекающего за один импульс, соответствует числу электронов, необходимых для восстановления того количества серебра, которое перекрывает площадь капилляра моноатомным слоем.
Кривая на рис. 2.1 отражает идеализированную зависимость v = f(ΔT). В реальных системах свой вклад в рост кристалла могут вносить двумерные зародыши при малых пересыщениях благодаря наличию примесей в среде или ступеней иного происхождения, в связи с чем можно наблюдать смещение кривой v(λ) - β влево.
В работах А. Н. Колмогорова и др. указывается, что зависимость нормальной скорости роста грани от пересыщения, в свою очередь, существенно влияет на размеры этой грани. К моменту появления нового зародыша на данном участке поверхности предыдущий разрастается до размера ~  , где Λ∞ ~ Δμ. Если размер грани кристалла
, где Λ∞ ~ Δμ. Если размер грани кристалла 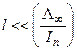 то ее нормальная скорость:
то ее нормальная скорость:
v(λ) ~ Inl2. (2.7)
При обратном неравенстве нормальная скорость:
v(λ) ~ а(Λ2∞ In)1 / 3 (2.8)
и не зависит от размера грани.
Существенно, что вокруг каждой ступени создается область пониженного пересыщения (nSO), где образование зародышей маловероятно.
Если передвигается эшелон параллельных ступеней (рис. 2.2), расстояние между которыми ∆r, то скорость движения одиночной ступени выразится:
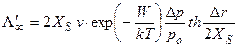 , (2.9)
, (2.9)
где 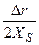 - величина отклонения поглощающей поверхности от вертикали. При Δr >> XS (угол θ мал)
- величина отклонения поглощающей поверхности от вертикали. При Δr >> XS (угол θ мал) 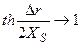 , и уравнение (2.8) сводится к (2.5). При Δr << XS (угол θ велик)
, и уравнение (2.8) сводится к (2.5). При Δr << XS (угол θ велик)  и соответственно
и соответственно  , т. е. скорость движения ступеней должна снижаться с уменьшением Δr.
, т. е. скорость движения ступеней должна снижаться с уменьшением Δr.
А. А. Чернов (1961) дает более точное выражение зависимости скорости движения ступени от Δr, с учетом времени релаксации τ, необходимого для восстановления равновесия вблизи ступени; времени жизни молекулы в состоянии адсорбции на поверхности τS; величины отклонения поглощающей поверхности от вертикали 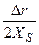 ; кинетического коэффициента кристаллизации ступени βСТ, характеризующего скорость обмена частицами между ступенью и адсорбционным слоем:
; кинетического коэффициента кристаллизации ступени βСТ, характеризующего скорость обмена частицами между ступенью и адсорбционным слоем:
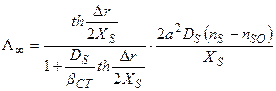 , (2.10)
, (2.10)
где 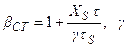 – степень пересыщения.
– степень пересыщения.
График зависимости 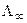 от Δr представлен на рис. 2.3. Кривая 1 соответствует малому значению βСТ по сравнению с величиной скорости поверхностной диффузии
от Δr представлен на рис. 2.3. Кривая 1 соответствует малому значению βСТ по сравнению с величиной скорости поверхностной диффузии  . Это имеет место, если кристаллизация затруднена, например, химической реакцией. Кривая 2 отвечает обратному соотношению двух скоростей
. Это имеет место, если кристаллизация затруднена, например, химической реакцией. Кривая 2 отвечает обратному соотношению двух скоростей 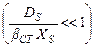 .
.
Нормальная скорость роста грани связана со скоростью движения ступени зависимостью:
 , (2.11)
, (2.11)
где 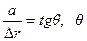 - угол отклонения вицинального холмика от ориентации плотноупакованной грани.
- угол отклонения вицинального холмика от ориентации плотноупакованной грани.
 |
Из вышеизложенного следует вывод: с уменьшением Δr (в области Δr < XS) увеличивается θ, сокращается величина Х0, увеличивается плотность изломов. Предельный случай (2.11), когда Δr = а, грань приобретает округлую форму, становится атомно-шероховатой и растет не послойным, а нормальным механизмом, при котором
 .
.
Исходя из соотношений (2.1), (2.2), (2.4), (2.10) и (2.11) получаем уравнение для нормальной скорости роста кристалла из паров:

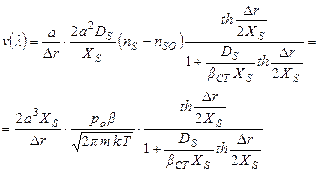 (2.12)
(2.12)
где 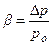 - относительное пересыщение (не смешивать с βСТ - кинетическим коэффициентом кристаллизации ступени).
- относительное пересыщение (не смешивать с βСТ - кинетическим коэффициентом кристаллизации ступени).
Графическое изображение зависимости и v(λ) от 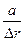 дано на рис. 2.4.
дано на рис. 2.4.
2) Дислокационный механизм роста.
В классической теории роста скорость перемещения идеально гладкой (плотноупакованной) грани растущего кристалла пропорциональна частоте появления на ней двумерных (плоских) зародышей (новых атомарных или молекулярных слоев). Разрастание слоя, или перемещение краев неукомплектованных зародышей, происходит достаточно быстро и можно думать, что оно не лимитирует скорости кристаллизации. Вероятность образования нового слоя ничтожна при пересыщениях ниже 25 – 50%. Однако реальные кристаллы растут с наблюдаемыми скоростями при пересыщении 1% или ниже, и большинство правильных и хорошо образованных кристаллов получается в действительности при низких пересыщениях. Все это указывает на то, что реальные кристаллы несовершенны.
Одно из несовершенств кристаллов – дислокации, обеспечивающие наличие готовых ступеней на поверхности плотноупакованной грани кристалла.
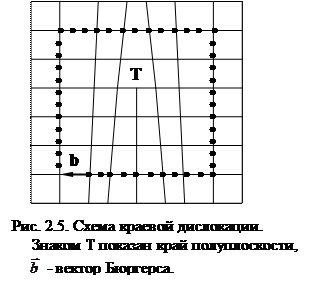 На любой плоскости идеальной решетки кристалла можно провести линию через ближайшие соседние атомы так, что она образует замкнутую плоскую петлю. Такая линия называется контуром Бюргерса. Подобная линия в реальном кристалле, имеющем геометрический дефект дислокационного типа, не образует замкнутой петли. Дислокация – это линейное несовершенство, для которого контур Бюргерса разомкнут; вектор, замыкающий разомкнутый контур, называется вектором Бюргерса (рис. 2.5 и 2.6).
На любой плоскости идеальной решетки кристалла можно провести линию через ближайшие соседние атомы так, что она образует замкнутую плоскую петлю. Такая линия называется контуром Бюргерса. Подобная линия в реальном кристалле, имеющем геометрический дефект дислокационного типа, не образует замкнутой петли. Дислокация – это линейное несовершенство, для которого контур Бюргерса разомкнут; вектор, замыкающий разомкнутый контур, называется вектором Бюргерса (рис. 2.5 и 2.6).
Различают краевые, винтовые, косые или криволинейные дислокации.
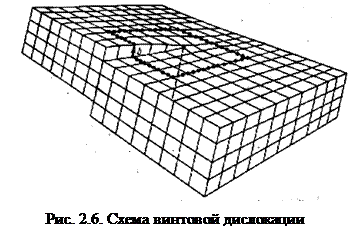
Краевую дислокацию удобно представить себе так, что в разрез кристаллической решетки вставлена добавочная полуплоскость (рис. 2.5). Край полуплоскости образует линию – ось дислокации, которая простирается вдоль всего кристалла. В краевой дислокации вектор Бюргерса перпендикулярен оси дислокации. Если вектор  параллелен оси дислокации ВВ′, определяют винтовую дислокацию (рис. 2.6). Краевые и винтовые дислокации – крайние разновидности дислокаций. Косые, или криволинейные, дислокации представляют собой промежуточные по ориентировке
параллелен оси дислокации ВВ′, определяют винтовую дислокацию (рис. 2.6). Краевые и винтовые дислокации – крайние разновидности дислокаций. Косые, или криволинейные, дислокации представляют собой промежуточные по ориентировке  относительно оси дислокации.
относительно оси дислокации.
Может быть вставлено несколько полуплоскостей, тогда вектор Бюргерса соответственно увеличивается. Дислокации различаются по знаку, в зависимости от того, «сверху» (+) или «снизу» (-) вставлена полуплоскость в случае краевой дислокации. В положительной винтовой дислокации движение вдоль контура Бюргерса от более высокого уровня к низкому происходит по часовой стрелке (см. рис. 2.6), в отрицательной – против часовой стрелки.
 Положительная и отрицательная винтовые дислокации дают начало спиралям роста, закручивающимся соответственно по часовой стрелке и против неё. Атомные плоскости в кристалле расположены вокруг оси дислокации по спирали по правому или левому винту. На расстояниях, превышающих несколько межмолекулярных расстояний от линии дислокации, искажение кристалла сглаживается.
Положительная и отрицательная винтовые дислокации дают начало спиралям роста, закручивающимся соответственно по часовой стрелке и против неё. Атомные плоскости в кристалле расположены вокруг оси дислокации по спирали по правому или левому винту. На расстояниях, превышающих несколько межмолекулярных расстояний от линии дислокации, искажение кристалла сглаживается.
Исходной позицией дислокационной теории роста является наличие в кристалле винтовых дислокаций. Дислокация характеризуется избыточной энергией, которая суммируется из энергии оборванных или искаженных связей в ядре дислокации и энергии слабых напряжений вокруг дислокаций (упругих напряжений). Энергия дислокации зависит от механических свойств кристалла и прямо пропорциональна квадрату вектора Бюргерса, который вдоль дислокации остается неизменным, поэтому дислокация не может кончаться в кристалле.
За счет избыточной энергии в области ядра дислокации вещество обладает повышенной химической активностью и поэтому рост, окисление, плавление и растворение всегда начинаются на дефектах и идут более интенсивно вдоль них.
Выходя на поверхность кристалла, винтовая дислокация создает незарастающую ступень, высота которой равна проекции вектора Бюргерса дислокации на нормаль к поверхности; если дислокация нормальна к поверхности, то высота ступени равна вектору Бюргерса.
Вблизи оси дислокации будет сказываться зависимость пересыщения от радиуса кривизны ступеньки. Ступень будет закручиваться в спираль до тех пор, пока радиус её у выхода дислокации не достигнет критического значения – радиуса критического зародыша. После этого вся спираль будет стационарно вращаться. Вначале ступенька перемещается параллельно самой себе. За счет большей скорости перемещения ступеньки вблизи оси винтовой дислокации произойдет искривление ступеньки и образование спирали. Искривленная часть ступеньки менее устойчива, так как ее радиус кривизны ρ мал, эффективное пересыщение тоже мало, следовательно, и скорость ее перемещения здесь уменьшится, пока не будет достигнуто равновесное состояние при ρ = ρк. Это состояние соответствует такой форме спирали, при которой все её части перемещаются с одинаковой угловой скоростью ω
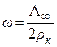 (2.13)
(2.13)
Здесь ρк – критический радиус кривизны двумерного зародыша, равный
 (2.14)
(2.14)
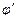 - удельная свободная краевая энергия.
- удельная свободная краевая энергия.
Тангенциальная скорость перемещения участка спирали с радиусом кривизны ρ при небольших пересыщениях равна
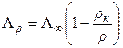 (2.15).
(2.15).
Если кривизна у точки выхода оси дислокации велика ρ< ρк, то рост в этом участке происходить не может, вследствие чего вдоль оси дислокации образуется в процессе роста кристалла полый пустой канал.
Различают круговые и полигональные спирали. Круговые спирали возникают в случае независимости скорости роста от кристаллографического направления. Это происходит, когда длина свободного пробега частицы XS>>X0 больше среднего расстояния между изломами. В такой ситуации частица, адсорбированная вблизи ступеньки, прилипнет к ступеньке независимо от ориентации последней. Полигональные спирали в соответствии с выраженной анизотропией скорости роста кристалла отражают симметрию грани. При этом линии ростовых фронтов располагаются преимущественно параллельно плотноупакованным направлениям на грани кристалла. Полигональные спирали возникают, если не выполняется условие XS>>X0 , так что изломы немногочисленны, далеко отстают друг от друга, и расстояния, на которые перемещаются адсорбированные частицы, малы. Часты промежуточные случаи, когда условия роста неблагоприятны для образования чисто круговых или полигональных спиралей.
Число оборотов спирали в 1с определяет активность спирали, равную 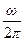 . По существу активность спирали – число ступеней, проходящих через данную точку за 1с. Активность характеризует мощность дислокации, как генератора ступеней, «выпускающего» витки с той или иной частотой. Расстояние между витками
. По существу активность спирали – число ступеней, проходящих через данную точку за 1с. Активность характеризует мощность дислокации, как генератора ступеней, «выпускающего» витки с той или иной частотой. Расстояние между витками 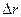 ((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228270']=__lxGc__['s']['_228270']||{'b':{}})['b']['_698049']={'i':__lxGc__.b++};
((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228270']=__lxGc__['s']['_228270']||{'b':{}})['b']['_698049']={'i':__lxGc__.b++};
Дата добавления: 2014-12-03; просмотров: 853; Мы поможем в написании вашей работы!; Нарушение авторских прав |