
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Физико-химические особенности наноструктурных материалов
Физико–химия твердотельных наноструктур как бы является мостиком между такими традиционными областями, как атомная физика, где изучают свойства отдельных атомов, и физико–химией концентрированного состояния, в рамках которого изучают твердотельные вещества, количество атомов в которых практически бесконечно. По сути, наноструктура – это очень маленький фрагмент твердого тела. Однако оказывается, что при таких малых размерах свойства наноструктур очень сильно отличаются от свойств объёмных материалов.
Задача нанотехнологии, если сформулировать ее кратко, – это создание низкоразмерных систем с размерами структурных элементов от долей до нескольких десятков нанометров. При этом имеются в виду как отдельные частицы с указанным диаметром, так и двумерные (например пленки) и одномерные (например, квантовые нити) структуры. Следует отметить, что с уменьшением размера частиц понятие фазы выражено менее четко: границы между гомогенной и гетерогенной фазами, между аморфными и кристаллическими состояниями определить трудно. Обычные физико-химические представления, включающие понятия «состав-свойства», «структура-функция» дополняются в этом случае терминами «размер», «самоорганизация».
Изучение различных свойств обособленных наночастиц составляет одно из направлений нанонауки. Другое направление связано с изучением расположения атомов внутри нанообъекта, формируемого из наночастиц. Относительная стабильность отдельных частей наноструктуры находится в зависимости от кинетических и термодинамических факторов. Наночастицы можно рассматривать как промежуточные образования между атомами с одной стороны, и твердым состоянием – с другой. Наночастицы и наносистемы обладают многими особенностями физико-химических свойств, не наблюдавшихся ранее в твердых телах.
Каковы основные причины, инициирующие необычные свойства у наносистем? В чем особенности таких нанообъектов? Нам представляется, что можно выделить два основных фактора, влияющих на формирование свойств наносистем – это изменение термодинамического состояния наносистем по сравнению с классическим и появление квантово-размерных эффектов с уменьшением характеристических размеров структурных элементов.
Теоретические и экспериментальные исследования термодинамики малых частиц показывают, что размер частиц является активной термодинамической переменной, определяющей вместе с другими термодинамическими переменными состояние системы. Вследствие столь малых размеров они имеют высокую величину поверхности раздела. Как следствие, такие нанообъекты проявляют высокую физико-химическую активность. Высокая реакционная способность наночастиц часто приводит к потере их индивидуальности.
Наночастицы размером менее 10 нм обладают избыточной энергией и высокой химической активностью. Частицы размером около 1 нм практически без энергии активации вступают в процессы агрегации, приводящие к образованию наночастиц металлов, и в реакции с другими химическими элементами, обуславливающие получение веществ с новыми свойствами. Зависимость химической активности от размера реагирующих частиц объясняют тем, что свойства индивидуальных атомов элементов и формируемых из атомов кластеров и наночастиц отличаются от свойств аналогичных макрочастиц. Образование наночастиц из атомов сопровождается двумя процессами: формирование металлических ядер разного размера и взаимодействие между частицами, которое способствует созданию из них ансамблей, представляющих наноструктуру. Избыточная энергия таких объектов определяется в первую очередь нескомпенсированностью связей поверхностных и приповерхностных атомов. Под термином «поверхность» или «межфазная граница» обычно понимают слой вещества конечной толщины, разделяющий объемные фазы. Его толщина, как правило, составляет несколько атомных слоев. Если количество вещества на поверхности в объеме становятся соизмеримыми, то роль поверхности как более активной составляющей существенно возрастает [14].
С изменением размеров частиц связан еще ряд термодинамических свойств наночастиц. Концентрация вакансий в наночастицах повышается с уменьшением их размера, одновременно снижаются температуры полиморфных превращений и параметры решеток, возрастает сжимаемость и растворимость. Экспериментальные и теоретические исследования термодинамики малых частиц позволяют утверждать, что размер частиц является активной переменной, определяющей вместе с другими термодинамическими переменными состояние системы и ее реакционную способность. Размер частиц можно рассматривать как своеобразный эквивалент температуры и в этом случае значение потенциала Гиббса будет отличаться от стандартных значений массивной фазы (рис.1).

Рис.1. Изменение свободной энергии Гиббса (G) бинарного наноструктурного сплава со средней концентрацией 5% от размера кристаллитов (L) . Для обычного кристалла G=4 кДж /моль [15]
Характер зависимости G=f(L) означает, что из-за существования минимума при Lкр рост кристаллитов в интервале L< Lкр становится термодинамически невыгодным.
Электронные свойства наноразмерных систем отличаются от известных объемных свойств материала, из которого они сделаны. Одной из основных особенностей низкоразмерных систем является модификация их электронной структуры при ограничении размеров системы в одном или нескольких координатных направлениях до размеров, сравнимых с длиной волны де-Бройля. В этом случае в направлении, где происходит ограничение размеров, имеет место переход от непрерывной электронной структуры валентной зоны к дискретной электронной структуре. Это связано, прежде всего, с проявлением квантово-механических явлений.
В классической физике электроны, как и все другие частицы, движутся по траекториям, которые можно рассчитать с помощью уравнений Ньютона. В квантовой механике картина движения электронов совершенно иная.
С позиции квантовой механики электрон может быть представлен волной, описываемой соответствующей волновой функцией. Распространение этой волны в наноразмерных твердотельных структурах контролируется эффектами, связанными с квантовым ограничением, интерференцией и возможностью туннелирования через потенциальные барьеры. Волновая функция (Ψ-функция) дает вероятностное, статистическое описание электрона в пространстве. Волна, соответствующая свободному электрону в твердом теле, может беспрепятственно распространяться в любом направлении. Ситуация кардинально меняется, когда электрон попадает в твердотельную структуру, размер которой L, по крайней мере в одном направлении, ограничен и по своей величине сравним с длиной электронной волны. Классическим аналогом такой структуры является струна с жестко закрепленными концами. Колебания струны могут происходить только в режиме стоячих волн с длиной волны 
 , где n = 1, 2,…
, где n = 1, 2,…
Аналогичные закономерности поведения характерны и для свободного электрона, находящегося в твердотельной структуре ограниченного размера или области твердого тела, ограниченной непроницаемыми потенциальными барьерами. На рис. 2 такая ситуация проиллюстрирована на примере квантового шнура, у которого ограничены размеры сечения a и b. В этих направлениях возможно распространение только волн с длиной, кратной геометрическим размерам структуры.

Рис. 2. Возможности для движения электронов в наноразмерной структуре.
Разрешенные значения волнового вектора для одного направления задаются соотношением  , где L в соответствии с рис. 2 может принимать значения, равные a или b. Для соответствующих им электронов это означает, что они могут иметь только определенные фиксированные значения энергии, то есть имеет место дополнительное квантование энергетических уровней. Энергия электрона имеет строго определенные, дискретные значения.
, где L в соответствии с рис. 2 может принимать значения, равные a или b. Для соответствующих им электронов это означает, что они могут иметь только определенные фиксированные значения энергии, то есть имеет место дополнительное квантование энергетических уровней. Энергия электрона имеет строго определенные, дискретные значения.
Это явление получило название квантового ограничения. Вдоль шнура могут двигаться электроны с любой энергией.
Запирание электрона с эффективной массой m*, по крайней мере в одном из направлений, в соответствии с принципом неопределенности приводит к увеличению его импульса на величину 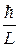 , где
, где  – постоянная Планка. Соответственно увеличивается и кинетическая энергия электрона на величину
– постоянная Планка. Соответственно увеличивается и кинетическая энергия электрона на величину 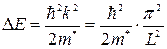 . Таким образом, квантовое ограничение сопровождается как увеличением минимальной энергии запертого электрона, так и дополнительным квантованием энергетических уровней, соответствующих его возбужденному состоянию. Это приводит к тому, что электронные свойства наноразмерных структур отличаются от известных объемных свойств материала, из которого они сделаны.
. Таким образом, квантовое ограничение сопровождается как увеличением минимальной энергии запертого электрона, так и дополнительным квантованием энергетических уровней, соответствующих его возбужденному состоянию. Это приводит к тому, что электронные свойства наноразмерных структур отличаются от известных объемных свойств материала, из которого они сделаны.
На рис.3 приведены примеры различного типа низкоразмерных систем, в которых ограничение волновых функций имеет место в одном координатном направлении (двумерные (2D) системы), в двух (одномерные (1D) системы) и во всех трех направлениях (нуль-мерные (0D) системы). В таких случаях говорят о системах пониженной размерности 2D-,1D- и 0D-типа.
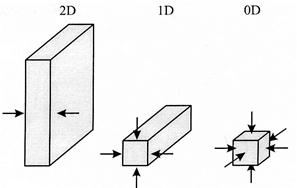
Рис.3. Пространственное ограничение волновых функций в двумерных (2D), одномерных (1D) и нуль-мерных (0D) системах.
Взаимодействие электронных волн в наноразмерных структурах как между собой, так и с неоднородностями в них может сопровождаться интерференцией, аналогичной той, которая наблюдается для световых волн. Отличительная особенность такой интерференции состоит в том, что благодаря наличию у электронов заряда имеется возможность управлять ими с помощью локального электростатического или электромагнитного поля и таким образом влиять на распространение электронных волн.
Уникальным свойством квантовых частиц, в том числе и электронов, является их способность проникать через преграду даже в случаях, когда их энергия ниже потенциального барьера, соответствующего данной преграде. Это было названо туннелированием. Схематически оно представлено на рис. 4. Будь электрон классической частицей, обладающей энергией E, он, встретив на своем пути преграду, требующую для преодоления большей энергии U, должен был бы отразиться от этой преграды. Однако как волна он хотя и с потерей энергии, но проходит через эту преграду.

Рис. 4. Туннелирование электрона с энергией E через потенциальный барьер высотой U, U > E.
Эта вероятность тем выше, чем геометрически тоньше барьер и меньше разница между энергией падающего электрона и высотой барьера. Квантовое ограничение, проявляясь в наноразмерных структурах, накладывает специфический отпечаток и на туннелирование. Так, квантование энергетических состояний электронов в очень тонких, периодически расположенных потенциальных ямах приводит к тому, что туннелирование через них приобретает резонансный характер, то есть туннельно пройти через такую структуру могут лишь электроны с определенной энергией.
Эти основные положения квантовой механики лежат в основе создание наноразмерных квантовых структур.
В целом у наносистем, начиная с определенного момента, появляется, т.н. размерный эффект, т.е. зависимость свойств наносистем от размера наночастиц. Размерный эффект Г. Гляйтер определил, как поведение материала, наблюдаемого в случае совпадения размера блока микроструктуры и некоторой критической длины, характеризующей явление (длина свободного пробега электронов и фононов, размер магнитных доменов, критический радиус дислокационной петли и др.). [13]
К наноматериалам относятся вещества не только потому, что они имеют малый характеристический размер структурного элемента, отвечающего за проявление того или иного свойства, а и потому, что характеристики данного свойства зависит от размера структурного элемента. Проявление размерного эффекта является характерной особенностью наноматериалов и является предметом систематических исследований [11, 15-18].
Размерная зависимость наиболее значимых для данного материала свойств позволяет ответить на такие вопросы: относится ли данный материал к классу наноматериалов и при каких размерах структурных элементов достигается максимальный выигрыш свойств у наноматериалов. Необходимо отметить, что свойства наноматериалов определяются не только размерностью структурного элемента , но и окружением, в которое помещен такой элемент (структура границ, межфазное натяжение и др.).
Некоторые размерно-зависимые свойства, наблюдающиеся у наноматериалов, представлены в табл.1.
Таблица 1
Размерная зависимость физических свойств наноматериалов
| Свойства | Отклик материала на уменьшение размера структурного элемента |
| Фазовые превращения | Понижение температуры фазовых превращений, в том числе температуры плавления |
| Кинетические | Аномально высокие значения коэффициентов диффузии, повышение теплоемкости, снижение теплопроводности |
| Электрические | Повышение электросопротивления, возрастание диэлектрической проницаемости |
| Магнитные | Возрастание коэрцитивной силы, магнитосопротивления, появление супермагнетизма |
| Механические | Повышение предела текучести, твердости, вязкости разрушения, износостойкости, проявление сверхпластичности при высоких температурах |
Кратко рассмотрим некоторые из них.
Температура фазового превращения в значительной степени определяется поверхностной энергией. Образования фаз с меньшей поверхностной энергией и более плотной упаковкой является предпочтительной, например, переход от менее плотной ОЦК структуры к более плотной ГЦК структуре при уменьшении размера частиц. Высокая поверхностная энергия в сочетании с малым размером зерна создают сжимающие напряжения в объеме зерна, что сдвигает фазовые равновесия в нанокристаллических материалах.
Для ряда металлов (Al, Ag, Au, Gd и др.) наблюдалось уменьшение параметров решетки при уменьшении диаметра наночастиц (рис.5). Значение межатомных расстояний непрерывно снижается с уменьшением размера частиц и составляет 90% значения компактного металла для частиц размером 1нм.

Рис.5.Относительное изменение периода решетки ∆а/а в зависимости от диаметра D наночастиц золота Au и серебра Ag [11].
Влияние размера наночастиц на параметр решетки отлично не только для металлов, но я для соединений. Как правило, это сопровождается фазовыми превращениями в соединениях [18]. Так, обычно орторомбический оксид иттрия становится кубическим, если размер зерна уменьшается до 10 нм. Диоксид циркония, обычно моноклинный, становится тетрагональным или кубическим; тетрагональный титанат бария становится кубическим. Для каждого вещества существует критический размер r частицы (нанокристаллита), ниже которого термодинамически стабильной становится другая фаза. Размерная зависимость среднего межатомного расстояния (∆а/а) можно выразить соотношением [15]:
 ,
,  , (1)
, (1)
где ∆d – среднее изменение межплоскостного расстояния; γ – поверхностное натяжение; σ – плотность свободной поверхностной энергии; kT – изотермическая сжимаемость; А – площадь поверхности.
Наиболее вероятной причиной уменьшения периода решетки малых частиц по сравнению с массивным веществом является нескомпенсированность межатомных связей атомов поверхности и, как следствие этого, сокращение расстояний между атомными плоскостями вблизи поверхности частицы. Вместе с тем, теоретические расчеты не дают однозначного ответа на вопрос, как должен меняться параметр кристаллической решетки нановещества в зависимости от размера наночастиц. По-видимому, возможно как увеличение, так и уменьшение параметра решетки при уменьшении размера наночастиц.
Изменение температуры плавления Тпл металлов в зависимости от размера частиц, по-видимому, один из первых эффектов, привлекших внимание исследователей. С уменьшением размера частиц Тпл металлов может понижаться на несколько сотен градусов. Например, Тпл «компактного» золота составляет 1340ºК, а при переходе к частицам размером 2 нм температура плавления понижается на 1000 градусов (рис.6).

Рис. 6. Зависимость температуры плавления золота от размера частиц: точки – экспериментальные данные; сплошная линия – расчетные значения [19].
Экспериментально уменьшение температуры плавления малых частиц наблюдалось и у других металлов (Sn, Pb, Cu, Al, Bi) и некоторых соединений. Зависимость Тпл от размера частиц металла рассматривается с позиций двух моделей: одна из них использует термодинамические представления, другая – колебания атомов.
С позиции термодинамики переход из твердого состояния в жидкое с ростом температуры начинается с появления на поверхности наночастиц бесконечно малого жидкого слоя, когда ее ядро остается твердым, что обусловлено поверхностным натяжением. Вторая модель предполагает предварительное существование жидкого слоя вокруг твердой частицы и равновесие такой системы в присутствии паровой фазы. Атомы поверхности связаны слабее и с повышением температуры это может привести к большим амплитудам колебаний при тех же температурах, чем у атомов, находящихся в объеме частиц. В любом случае можно считать установленным, что у свободных наночастиц металлов всегда наблюдается понижение Тпл с уменьшением их размера.
Из рассмотрения условий равновесия жидкой капли с ее насыщенным паром вытекает обратно пропорциональная зависимость Тпл жидкой капли от ее размера. Для описания размерной зависимости Тпл наночастиц предложен ряд выражений [12], например:
Тпл (r) = Тпл (1-α/r), (2)
где r – размер наночастицы, α – постоянная, зависящая от плотности и температуры плавления материала и его поверхностной энергии.
Размерная зависимость Тпл наночастиц сказывается и на диаграммах состояния с участием нанокомпонентов, в частности, на значениях эвтектических или монотектических температур бинарных систем [15].
Рассчитанные значения температур эвтектик показали, что в системе TiN – AlN температура плавления эвтектического состава уменьшается с 2715 до 2110 К, а в системе Ti – TiB2 – от 2870 до 2420 К, при уменьшении компонентов до 20 нм [18].
Еще один интересный аспект термодинамики нанокристалов – это пограничные сегрегации и пересыщенные фазы.
Кинетические свойства, такие как диффузионная подвижность, теплопроводность и др., существенно зависят от размера структурного элемента.
Для многих металлов (Pd, Cu, Ni, Ag и др.) в наноструктурном состоянии наблюдается повышение теплоемкости и увеличение коэффициентов термического расширения, уменьшение теплопроводности, температуропроводности (рис.7).

Рис. 7. Температурная зависимость теплоемкости наночастиц Pd диаметром 3,0 нм (1) и 6,6 нм (2) и массивного палладия (3) [11].
По-видимому, одна из причин повышения теплоемкости наноструктурированных металлов обусловлена вкладом зернограничной фазы, которая имеет уменьшенную температуру Дебая и повышенную теплоемкость по сравнению с крупнозеренным материалом.
В наноматериалах резко возрастает (на 3 порядка и болеее) значение коэффициентов пограничной диффузии и самодиффузии.
Многими исследователями обнаружено значительное повышение удельного электросопротивления нанокристаллических Сu, Pd, Fe, Ni и различных сплавов при уменьшении размера зерен [11, 15].
Одно из соотношений, связываюшее удельное сопротивление ρ нанокристаллического материала с величиной зерна D имеет вид [11]:
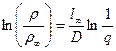 , (3)
, (3)
где ρ∞ - удельное електросопротивление крупнозеренного вещества; l∞ - длина свободного пробега электронов в бездефектном монокристалле; q – коэффициент рассеяния электронов при перходе межзеренных границ. Поскольку коэффициент рассеяния 0 < q < 1, то из выражения (3) следует, что с уменьшением размера зерен сопротивление нанокристаллического материала должно расти. Основная причина повышения электросопротивления у нанокристаллических металлов – это увеличение рассеяния электронов на границах зерен.
Размерно–зависимые характеристики проявляются в диэлектриках и магнетиках. Изучение магнитных характеристик стимулируется значительными прикладными успехами в создании магнитных материалов в наносостоянии и этому вопрсу посвящено много работ [10, 11, 16, 18]. Размерная зависимость свойств проявляется на таких характерисиках, как коэрцитивная сила, остаточная намагниченность, магнитосопротивление. При определенных размерах нанокластеров (1÷10 нм) проявляется явление супермагнетизма.
Одно из важных направлений в исследовании наноматериалов – изучение размерной зависимости механических характеристик наноматериалов (твердости, прочности, пластичности, упругости и др.) Экспериментальные исследования механических свойств наноматериалов показали, что предел прочности, твердость многих металлов (Pd, Cu, Ag, Ni и др.) значительно выше, чем в соответствующих крупнозернистых аналогах [16, 20, 21,23]
Почему это происходит?
Увеличение твердости и прочности с уменьшением размера зерна до некоторого критического размера практически характерно для всех кристаллов. Это вытекает из известного уравнения Холла-Петча, что предел текучести 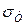 зависит обратно пропорционально от среднего размера зерна
зависит обратно пропорционально от среднего размера зерна 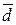 [22]:
[22]:
 , (4)
, (4)
где  - предел текучести монокристалла,
- предел текучести монокристалла,  - некоторый размерный коэффициент.
- некоторый размерный коэффициент.
Соотношение (4) достаточно хорошо выполняется в широком диапазоне значений 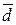 вплоть до 1 мкм. Значения
вплоть до 1 мкм. Значения  , полученные экстраполяцией в область размера
, полученные экстраполяцией в область размера 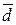 <100 нм в 2-3 раза превышают таковые для традиционных материалов [20, 21].
<100 нм в 2-3 раза превышают таковые для традиционных материалов [20, 21].
Экспериментальные результаты, полученные на нанокристаллах, показывают, что они значительно прочнее крупнозернистых аналогов. Нанофазные Cu, Pd, Fe с размером зерна ~5 нм, полученные компактированием ультрадисперсных порошков, показали значения твердости в 2-5 раз выше, чем у образцов с обычным размером зерна (рис. 8).

Рис. 8. Влияние размера зерна (d) на микротвердость металлов [23]
Рост твердости наблюдали также и у других нанофазных металлов (Ni, Ti, As и др.) и различных соединений (TiAl, Nb3Al, SiC, TiN, ZrO2 и др.) [16, 20]. При этом рост твердости и прочности у наноматериалов практически не зависит от способа их получения. Например, у нанокристаллов, полученных кристаллизацией из аморфного состояния, также наблюдалось повышение твердости как у однокомпонентных, так и многокомпонентных наноматериалов [16].
Можно констатировать, что твердость металлов и керамических материалов возрастает по мере того, как размер зерна переходит в нанофазную область. Однако величина размера зерна, до которой происходит упрочнение, зависит от ряда факторов и природа ее не совсем ясна. Обычно соотношение Холла-Петча (4) выполняется для значительной части исследованных наноматериалов лишь до определенного размера зерна, а при более низких его значениях наблюдаются обратные эффекты: твердость (прочность) падает по мере снижения размера зерна (рис. 9).
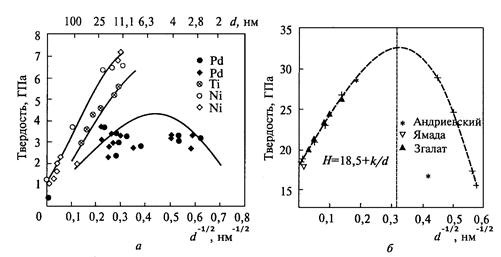
Рис. 9. Зависимость микротвердости различных материалов от размера зерна: металлов (а); керамики (б) [20]
В настоящее время не совсем ясно, соответствуют ли значения твердости, полученные для реальных компактированных наноматериалов, идеально плотным наносистемам.
Поведение наноматериалов в данном случае может быть замаскировано вкладами от остаточной пористости – трещинами и др. дефектами, возникающими в наноматериалах вследствие особенностей методов их получения.
Вопрос о природе микродефектов, возникающих в наноматериалах, и их роли в формировании свойств остается в значительной степени открытым. В частности, не совсем ясным является проявление дислокационного механизма в процессе деформации наноматериалов.
С одной стороны, размер кристаллитов в наноматериалах часто оказывается меньшим характерного размера петли Франка-Рида  (
(  , где G – модуль сдвига, b – вектор Бюргерса, τкр – критическое напряжение сдвига). При обычных значениях
, где G – модуль сдвига, b – вектор Бюргерса, τкр – критическое напряжение сдвига). При обычных значениях  и
и  нм величина
нм величина  нм и размножение дислокаций с помощью этих источников оказывается подавленным. С другой стороны, в наноматериалах, особенно полученных методами интенсивной пластической деформации, велика роль зернограничных дислокаций и дислокаций несоответствия.
нм и размножение дислокаций с помощью этих источников оказывается подавленным. С другой стороны, в наноматериалах, особенно полученных методами интенсивной пластической деформации, велика роль зернограничных дислокаций и дислокаций несоответствия.
Теоретически был оценен характерный размер свободного нанокристалла L*, ниже которого вероятность существования внутри кристалла подвижных дислокаций уменьшается [24]:
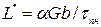 , (5)
, (5)
где α – коэффициент, зависящий от геометрии дислокаций и изменяющийся в пределах  ;
; 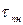 – напряжение Пайерлса-Набарро. Оценки L* для Cu, Al, Ni, Fe приводят к значениям в интервале
– напряжение Пайерлса-Набарро. Оценки L* для Cu, Al, Ni, Fe приводят к значениям в интервале  нм. Систематические исследования дислокаций в наноматериалах не очень многочисленны.
нм. Систематические исследования дислокаций в наноматериалах не очень многочисленны.
Можно полагать, что роль дислокаций в пластической деформации НМ пренебрежительно мала. При этом они часто представляют собой неподвижные (сидячие) конфигурации, что, по- видимому, является одной из причин того, что наноматериалы при испытании на растяжение обнаруживают весьма низкую пластичность.
Определяющую роль в аномалиях механических свойств наноматериалов играют, по всей вероятности, границы зерен. Природа границ раздела вообще и, в особенности, применительно к наноматериалам, продолжает оставаться предметом дискуссий [15]. В простейшем случае нанокристаллический материал, состоящий из атомов одного сорта, содержит два компонента, различающих по структуре: упорядоченные зерна (кристаллиты) размером 5 ÷ 20 нм и межкристаллитные границы до 1,0 нм. На рис. 10 представлена простейшая двумерная модель наноструктуры с нанокристаллитами разного размера и ориентации.

Рис.10. Двумерная модель нанокристаллического материала [1]. Нанокристаллиты с разной ориентацией изображены в виде черных кружков, межфазные границы – в виде светлых кружков.
Ширина границ раздела, определенная разными методами на различных нанокристаллических материалах, составляет от 0,4 до 1,0 нм [11]. Атомная структура границ не является простой и зависит от многих параметров: взаимной ориентации соседних кристаллов, типом межатомного взаимодействия и т.д. Атомная плотность межфазных границ на 20 ÷ 40 % меньше плотности нанокристаллитов, что по-видимому, является результатом несоответствия структур различных нанокристаллитов, развернутых хаотично друг относительно друга. Поскольку кристаллиты, формирующие нанокристаллический материал, ориентированы случайно, то таких границ, имеющих различное состояние, может быть порядка 1019 см-3 [1].
Объемная доля границ зерен у наноматериалов возрастает по мере снижения размера зерна, а затем снижается. В тоже время объемная доля тройных стыков зерен постоянно растет (рис. 11).

Рис. 11. Зависимость объемной доли границ зерен и тройных стыков от размера зерна (при толщине границы зерна 1 нм) [23].
Объемные доли межзеренной и внутризеренной (совершенной) компоненты равны при размерах зерна ~ 5 нм. При уменьшении размера зерна до 2 нм вклад объемной доли межзеренного вещества (с учетом тройных стыков) может составлять 80-90%. В этом случае структурное состояние межзеренных или межфазных границ существенным образом отличается от структурного расположения атомов в кристаллах.
Важным фактором, определяющим механическое поведение наноматериаов, являются внутренние напряжения. Они всегда имеются в наноматериалах из-за большого числа близко расположенных границ зерен и тройных стыков зерен. Кроме того, внутренние напряжения могут возникать вследствие особенностей методов получения наноматериалов. Наличие высоких внутренних напряжений у нанокристаллов приводит также к изменению атомной структуры наноматериалов. В частности, обнаружено изменение межатомных расстояний в кристаллической решетке, снижение координационного числа с уменьшением размера зерен наноматериалов [15, 25].
Изучение особенностей распространения трещин в наноматериалах представляется важным в связи с возможностью повышения значения трещиностойкости (вязкости разрушения) К1С хрупких наноматериалов. Имеющиеся на этот счет сведения пока противоречивы, хотя данные о повышении вязкости многофазных керамических нанокомпозитов являются обнадеживающими [16]. Хрупкие материалы (интерметаллиды, нанокерамика) становятся пластичными ниже критических размеров. У керамических наноматериалов обнаружена повышенная пластичность при низких температурах, ее можно использовать в промышленных процессах экструзии и прокатки [23]. Значительный практический интерес представляет температурная стабильность наноматериалов, явление сверхпластичности. За счет перехода к наносостоянию для некоторых систем (Ni3Al, TiO2, ZrO2 и др.) температурный интервал проявления сверхпластичности удалось снизить на 300-400 ˚С по сравнению с обычными мелкозернистыми материалами, но в целом эти вопросы требуют дальнейшего выяснения.
Дата добавления: 2014-11-13; просмотров: 915; Мы поможем в написании вашей работы!; Нарушение авторских прав |