Постулаты специальной (частной) теории относительности. Преобразования Лоренца

Эйнштейн сформулировал два постулата, лежащие в основе специальной теории относительности:

1. Физические явления во всех инерциальных системах отсчета протекают одинаково. Никакими физическими опытами, проведенными внутри замкнутой инерциальной системы отсчета, нельзя обнаружить, покоится ли эта система или движется равномерно и прямолинейно.

2. Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от скорости движения источника света или наблюдателя.

Наличие этих постулатов позволяет получить новые преобразования координат, отличающиеся от (7.1).

Пусть система движется относительно инерциальной системы K с постоянной скоростью v_о(рис. 7.1) так, чтобы оси x и 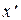при движении совпадали, а оси y, и z, 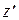были параллельны друг другу, причем вектор, соединяющий начала координат, , где t время. Можно показать, что координаты y и z связаны формулами y = ; z = 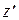. Ищем зависимость между подвижными и неподвижными координатами x в виде

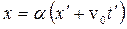, (7.2)

где a искомый коэффициент. Согласно первому постулату в силу равноправия систем отсчета для перехода от неподвижной системы отсчета к подвижной зависимость между координатами должна иметь аналогичный вид и отличаться лишь знаком для скорости v_o:

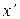= a(x - v_o, t). (7.3)

Пусть в моменты времени t = 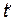= 0 в точке x = 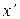= 0 в направлении оси x испускается вспышка света. Это событие через время t будет наблюдаться в точке x = ct и через время 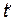в точке 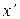= c 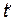. Здесь используется тот факт, что скорость света c для вакуума согласно 2^му постулату Эйнштейна одинакова в обеих системах. Подставляя в два последних равенства выражения (7.2) и (7.3), получим a(c + v_o) 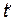= ct ; a(c - v_o)t = c 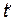. Перемножая эти два равенства, получим a = 1/(1 - b ²)^0,5 , где величину b = v_o /c называют относительной скоростью.

Исключая из равенств (7.2) и (7.3) координату x, получим

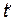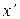t = /a + b /ac

Подставляя в эту формулу и в формулу (7.2) выражения для a и b, получим окончательно формулы для связи координат и времени :

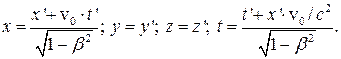(7.4)

Полученные формулы называют преобразованиями Лоренца. Ученый Лоренц впервые получил эти формулы и показал, что если уравнения Максвелла преобразовать подстановкой (7.4), то их вид останется прежним и эти уравнения подчиняются принципу относительности. Эйнштейн предположил, что все физические законы не должны меняться от преобразований Лоренца.

Преобразования Лоренца при малых скоростях движения (b ® 0) переходят в преобразования Галилея, которые являются предельным случаем преобразований Лоренца. Из преобразований Лоренца следует, что как пространственные, так и временные преобразования не являются независимыми. Таким образом, теория Эйнштейна оперирует не с трехмерным пространством, а рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство-время.

Теорию относительности часто называют релятивистской теорией, а специфические явления, описываемые этой теорий, - релятивистскими эффектами.