Полная физико-математическая постановка задачи о нестационарной теплопередаче через многослойное ограждение.

Рассмотрим полную физико-математическую постановку задачи нестационарной теплопередачи через многослойное ограждение.

На рисунке показана схема конструкции с обозначением слоев (1, 2, 3) и характерных границ, соответствующих внутренней 1 и внешней IV поверхностям ограждения и стыкам материальных слоев в его толще.

Задача состоит в отыскании изменения температуры t(z, х) и тепловых потоков q(z, х) во времени z и в пространстве по толщине ограждения х.

Для решения любой задачи нестационарной теплопередачи должны быть заданы: а) начальные условия, определяющие распределение температуры в толще и на границах ограждения в начальный момент времени; б) уравнения теплопроводности, описывающие процесс передачи тепла через толщу конструкции; в) граничные условия, определяющие условия теплообмена на всех характерных поверхностях.

Начальные условия обычно задаются в виде уравнения (таблицы, графика) распределения температуры в момент начала процесса, т. е. при z = 0. В общем случае, оно записывается в виде

Могут быть задачи без начальных условий, например при периодически повторяющихся условиях теплообмена на границах.

Уравнения теплопроводности в толще ограждения могут быть записаны в двух вариантах.

Вариант А - нелинейное уравнение теплопроводности с переменными коэффициентами

где сρ(х), λ(х) - заданные значения коэффициентов теплоемкости и теплопроводности отдельных материальных слоев в конструкции, ступенчато изменяющиеся от слоя к слою; в общем случае эти коэффициенты могут быть заданы изменяющимися по определенному закону в пределах каждого слоя, переменными во времени, зависящими от температуры.

Вариант Б - система линейных дифференциальных уравнений с постоянными коэффициентами; каждое уравнение записано для отдельного слоя с дополнительными условиями на границах - стыках материальных слоев:

для слоя 1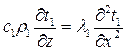

для слоя 2

для слоя 3

На границе II (на стыке между слоями 1 и 2) задано граничное условие IV рода, которое, как известно, определяется равенством теплоdых потоков

и температур t₁=t₂.

Такое же условие на границе III (на стыке между слоями 2 и 3):

и t₂=t₃.

Граничные условия частично рассмотрены при записи основных уравнений по варианту Б. Кроме записанных условий должны быть записаны условия теплообмена на внутренней и наружной поверхностях ограждения, соприкасающихся с внутренним t_B и наружным t_H воздухом и окруженных другими поверхностями, имеющими температуру t_R . Конвективный теплообмен определяется коэффициентом а_к и лучистый а_л. Нужно также учитывать, что ограждения могут облучаться сосредоточенными источниками тепла (солнца, нагретая печь в помещении и др.). Количество поглощенного поверхностью лучистого тепла может быть определено так:

где р- коэффициент поглощения поверхности ограждения для данного излучения; q - интенсивность падающего на ограждение излучения.

В общем случае на поверхностях ограждений происходит сложный теплообмен, определяемый условиями II (заданная интенсивность теплового потока) и III (заданные условия теплообмена с окружающей средой) рода. На границе 1 (индекс в) условие имеет вид

На границе IV (индекс н)

Обычно в помещениях условия лучисто-конвективного теплообмена учитываются единым коэффициентом теплообмена ав, отнесенным, например, к температуре воздуха tв. В этом случае запись условия на внутренней границе упрощается и имеет вид

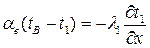
Подобное упрощение с использованием коэффициента теплообмена ан может быть сделано в записи граничного условия на наружной поверхности для зимних условий. При расчете теплообмена летом необходимо учитывать солнечное излучение, поэтому уравнение условия на границе IV для летнего периода обычно записывают в виде

Часто оказывается удобным заменить смешанное граничное условие II и III рода, каким является последнее уравнение, условием III рода с условной температурой наружной среды tусл в виде

Для определения значения температуры tусл приравняем левые

части двух последних уравнений и получим

Граничные условия на внутренней и наружной поверхностях ограждения могут быть заданы уравнением одного из трех приведенных видов. Выбор вида уравнения определяется конкретными условиями задачи и принятыми методами ее решения.