Геометрическая интерпретация задачи линейного программирования

Рассмотрим следующую задачу линейного программирования[16]:

На рис. 4.1 представлено множество допустимых точек, удовлетворяющих всем ограничениям задачи и представляющее собой пересечение полуплоскостей, отражающих ограничения задачи линейного программирования.

Рис. 4.1. Геометрическая интерпретация решения задачи

Геометрическую интерпретацию имеют ЗЛП с двумя переменными.

Исследуем целевую функцию 30х₁ + 40х₂. Данной целевой функции соответствует семейство прямых 30х₁ + 40х₂ = L, представляющих собой множество параллельных прямых, каждая из которых соответствует определенному значению параметра L. Тогда задачу линейного программирования можно сформулировать следующим образом. Найти такое максимальное значение L, при котором прямая 30х₁ + 40х₂ = L пересекает допустимое множество.

В общем случае с геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на которой достигается самая верхняя (нижняя) линия уровня (прямая, отражающая целевую функцию), расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Для нахождения экстремального значения целевой функции при графическом решении ЗЛП используют вектор-градиент целевой функции Ñf(`X) на плоскости Х₁ОХ₂. Этот вектор показывает направление наискорейшего изменения целевой функции, он равен

,

где 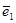и - единичные векторы по осям ОХ₁ и ОХ₂ соответственно. Таким образом, Ñf(`X) = (¶f/¶x<sub>1</sub>, (¶f/¶x<sub>2</sub>). Координатами вектора-градиента целевой функции Ñf(`X) являются коэффициенты целевой функции f(`X).

В рассматриваемом примере, если двигать прямую 30х₁ + 40х₂ = L из начала координат по направлению вектора-градиента целевой функции, то точкой, в которой достигается самая верхняя линия уровня является точка М пересечения прямых 5x₁ + 2x₂ = 10000 и x₁ + 2x₂ = 4000 с координатами x₁ = 1500 и x₂ = 1250. Таким образом, оптимальное решение достигается в точке М (1500; 1250). При этом значение целевой функции составит f(`X^*) =30 * 1500 + 40 * 1250 = 95000.

На этом примере можно увидеть основные свойства задач линейного программирования: допустимое множество точек представляет собой выпуклый многоугольник, получившийся в результате пересечения полуплоскостей и наибольшее значение целевой функции достигается в его вершине – крайней точке.

Решение задачи линейного программирования может быть не единственным, а состоять из бесконечного числа точек.

Таким образом, решение задачи линейного программирования состоит в следующем: необходимо построить многоугольник допустимых точек, найти его вершины и выбрать из них те, координаты которых придают максимальное значение целевой функции.