Метод искусственного базиса

При решении задач симплексным методом необходимо, чтобы модель задачи была канонической и система ограничений была приведена к единичному неотрицательному базису. Встречаются случаи, когда эти преобразования оказываются громоздкими[19].

Метод искусственного базиса дает возможность решать задачи, приведенные к каноническому виду, без предварительного нахождения опорного решения. Дана задача линейного программирования:

,

.

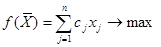
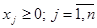Из этой задачи составим вспомогательную задачу следующим образом:

1) систему ограничений вспомогательной задачи получаем из системы ограничений исходной, добавляя в каждое ограничение, не содержащее базисную переменную, искусственную базисную переменную;

2) целевая функция равна алгебраической сумме искусственных переменных, взятых с коэффициентом (-1);

3) условие неотрицательности распространяется на все переменные, в том числе и искусственные.

Математическая модель вспомогательной задачи:

,

.

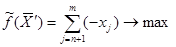
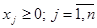Система ограничений вспомогательной задачи приведена к единичному базису, поэтому она имеет решение:

= (0, 0, ¼, 0, b₁, b₂, ¼, b_n),

при этом £ 0.

Между оптимальным решением вспомогательной задачи и опорным решением исходной задачи существует зависимость:

1) если = 0 достигается при = (l₁, l₂, ¼, l_n, 0, 0, ¼, 0), то = (l₁, l₂, ¼, l_n) является исходным опорным решением;

2) если max £ 0, то ограничения исходной задачи несовместны.